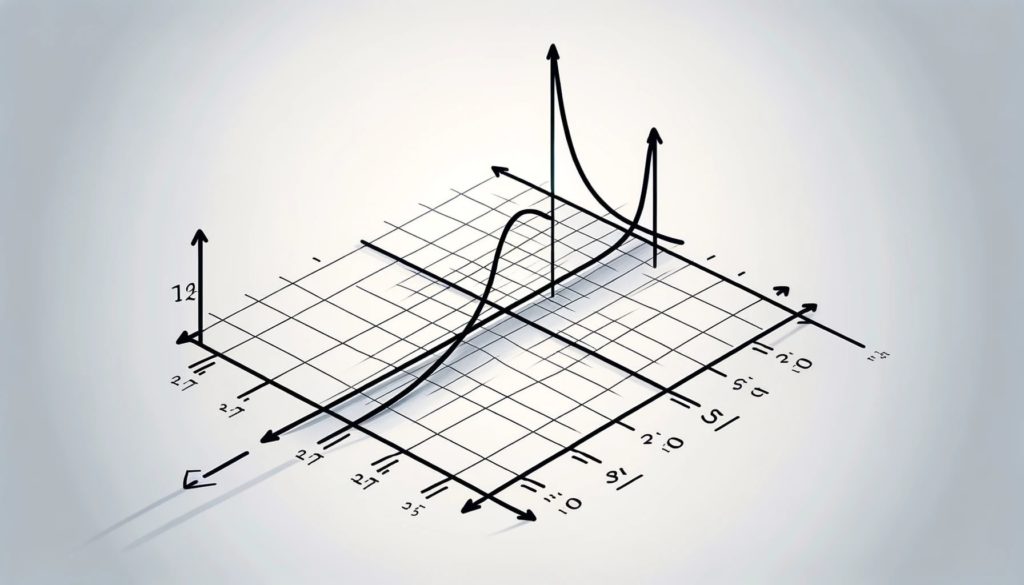
The relationship between horizontal and oblique asymptotes is as follows: horizontal asymptotes are special oblique asymptotes. Therefore, every horizontal asymptote is an oblique asymptote, but not every oblique is horizontal.
This can and should be used to shorten the computing of function asymptotes. There are two basic approaches to this topic:
1. First, we compute the horizontal asymptotes
The condition for the existence of a horizontal asymptote of a function is:
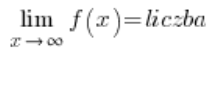or 
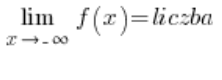
If we get horizontal asymptotes, we no longer count the diagonal ones (because it’s as if we already had the diagonal ones – we remember that horizontal is diagonal). However, if we don’t get the horizontal ones, we have a problem – we have to recalculate the diagonal asymptotes.
Of course, the situation is a bit more complicated: a horizontal asymptote may occur in
, and “don’t appear” in
. In such a case, we would not investigate the existence of an oblique asymptote in (because it’s already there), but we would have to investigate its existence in .
2. First, we compute the diagonal asymptotes
…and then the horizontal asymptotes will appear (or not) automatically, we just need to interpret the answers correctly. The downside is that the conditions for the existence of an oblique asymptote of a function are slightly more complicated:
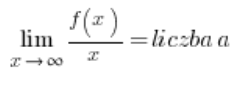and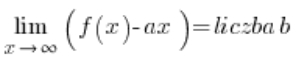 
or:
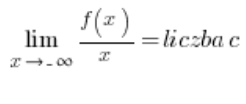and 
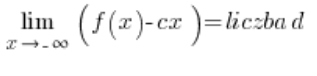
…and the advantage is that once we compute them, we don’t have to compute anything further. If the conditions are met and the number
(or
) from the conditions for the existence of an oblique asymptote will be equal
, this means that the oblique asymptote is a horizontal asymptote.
To further shorten your work, you can immediately calculate:
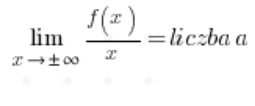and 
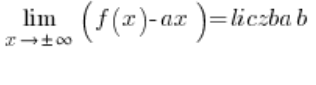
And the breakdown into counting separately the conditions for
and
only when necessary (when it will make a difference in the outcome of whether x tends to , or to .
