No products in the cart.
Krystian Karczyński- 3 July 2024
- Komentarz 0
There are times in life when the region of integration in a double integral is an ellipse….
What do we do then?
Elliptical Coordinates
A neat method of solving this is usually to use the so-called elliptical coordinates. It’s something like polar coordinates, the mechanism works in a similar way, only you substitute different things for x and y, and the Jacobian is different. The interpretation of ‘r’ is also different. So, to sum up, if you know how to switch to polar coordinates (which is usually done when the region of integration is a circle), you’ll easily get the hang of elliptical coordinates too.
So we have the integral: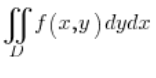 
and the region of integration bounded by an ellipse centered at the origin, with the equation: 
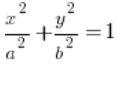. Let’s make sure the right side of the ellipse equation is 1, alright? If, for example, it’s 9, you can easily make it 1 by dividing both sides of the equation by 9.
The region of integration drawn looks like this:
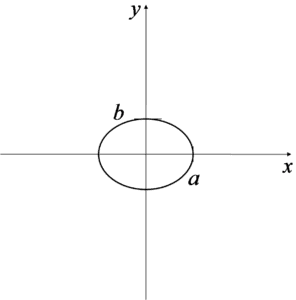
What a and b mean is clear from the drawing. Be careful, because if the denominator in the ellipse equation under 
is, for example, 9, it means that 
, for obvious reasons, right?
Now with such a “clean” situation, we move to elliptical coordinates, substituting:
Meaning of Variables in Elliptical Coordinates
The angle 
means exactly the same as in polar coordinates, and 
means something different. In basic problems with an ellipse given by a neat equation 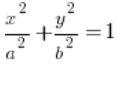, simply assume that ranges from zero to one (in more complex cases, substitute and into the ellipse equation and calculate the upper limit of r).
Jacobian
The Jacobian in elliptical coordinates is equal to 
.
Remembering the Jacobian, we switch to the integral in elliptical coordinates:
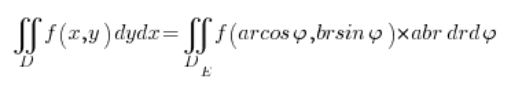
where the variables and are bounded: in the range from zero to one, and depending on whether we are talking about the whole ellipse, half of it, or, for example, a quarter – just like in polar coordinates.
Just take it and calculate.
Example
Calculate the integral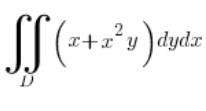 
, where D is the ellipse with the equation: 
.
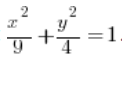Following the above scheme, we substitute:
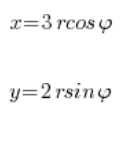
We take the region of integration:
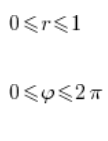
And calculate the integral:
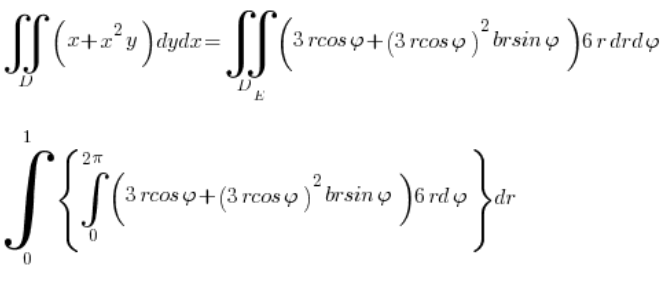
Which is, of course, just a formality by now 🙂
