Assumptions of the Classic Method of Least Squares. And why classic?
Joanna Grochowska-Angielczyk
Learning Department Manager.
Graduated in Financial Mathematics and Computer Science and Econometrics from the University of Bialystok. Experienced tutor in mathematical and economic subjects. Associated with eTrapez since 2015.
She lives in Bialystok, Poland. She loves to travel and hike in the mountains. She enjoys meetings with friends, experiments in the kitchen and volleyball.
Econometrics Lecture 7
Topic: Classical Method of Least Squares – assumptions
This lecture will be devoted to the Classical Method of Least Squares. You can of course also come across the name Classical Linear Regression Model, KMRL for short. Both names are correct and both are safe to use.
I will present and briefly discuss all the basic assumptions of this method. They mainly concern certain properties of the random component.
It is worth knowing these assumptions, because very often this issue appears on the econometrics exam, but not only. I remember well that mentioning the assumptions of KMNK happened to me as one of the questions during the defense of my BA thesis 🙂
So I invite you to read!
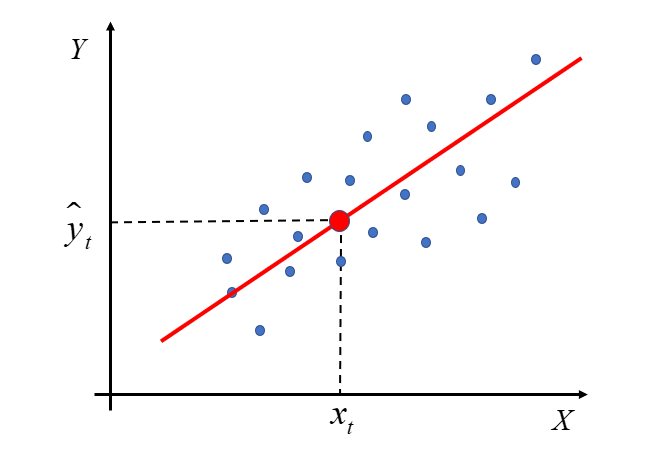
Let me start from the beginning, i.e. from the name itself. In the previous lecture the method of least squares was discussed. Its essence is best reflected in the example of a model with two variables – the explained one Y and one explanatory x The classic method of least squares is simply to determine under all conditions the applicability of OLS to estimate a vector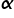 
in the model
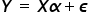
Here I will deal with the first part of the assumptions of the Classical Method of Least Squares. They are very important, because only when these assumptions are met, i.e. the actual data collected for the econometric model have the following properties interchangeably, only then can the model be built and the least squares method can be used to estimate the model parameters.
There are, of course, other methods of estimating model parameters, which have their own predetermined “guidelines”, e.g. the generalized method of least squares (UMNK), the method of maximum likelihood (MNW), the method of binomial regression, etc.
The assumptions of the KMNK are as follows:
- The estimated econometric model is linear with respect to the parameters .
- Explanatory variables are non-random quantities with fixed elements.
- Matrix row is equal to the number of estimated parameters, i.e .
- The sample size is larger than the number of estimated parameters, i.e. .
- There is no phenomenon of collinearity between explanatory variables.
- The expected value of the random term is zero: .
- The random component has a constant finite variance ;
- There is no phenomenon of autocorrelation of the random component, i.e. dependence of the random component in different time units .
- Random component has n -dimensional normal distribution: For t=1,2,…,n.
Note that there are a lot of them.
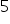Perhaps you had less of them written down in your classes. For example, assumption and result from assumption no 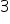so they may have been omitted. Often, the last four random components are combined into one sub-clause.
I will now try to explain in more detail the meaning of each of the assumptions.
Assumption 1. The estimated econometric model is linear with respect to the parameters .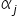
In one of the previous articles , I explained when an econometric model is linear with respect to parameters and when it is linear with respect to variables. Here, linearity with respect to unknown parameters is important .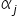
In general, in a typically linear model, the sum of type products plays the main role 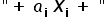. That is, both parameters and variables should be in prime powers at the same time, and the dependent variable Y should be a linear combination of explanatory variables and various parameters.
Hence, such a model can be written in matrix form: .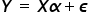
Vector 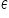is a vector of random components (individual observations) representing the combined effect of all secondary, random factors not included among the explanatory variables. Addition to the deterministic component of the random disturbance vector 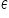is to model the fact that the recorded observations may differ in value from the values resulting from the theoretical construction of the economic model. Vector 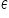groups random components that are by definition unobservable, we postulate their existence to explain any discrepancies between the theoretical values of the dependent variable and the observed values. In theory, if we know how many significant explanatory variables ( k ) there are and if we know what the form of the relationship is (linear), i.e. if Z1 is true, then the epsilon includes only random, secondary, disturbing factors. In practice, however, you have to take into account that the random component also includes the consequences of the following errors:
1. specification error (significant variable omitted, irrelevant variable included, etc.)
2. approximation error (if the form of the dependence is different, i.e., e.g. significantly non-linear, and it is not
approximated in a linear form).
In practice, we take into account that Z1 is not perfectly satisfied (but we can assume that we have chosen the explanatory variables well and that the true form of the relationship is well approximated by the linear relationship…). More precisely the property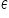 will be described in points Z6-Z9.
Assumption 2. Explanatory variables 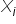are non-random quantities with fixed elements.
The explanatory variables are non-random. Their values are treated as constants in repeated trials.
The information contained in the sample is the only basis for estimating the structural parameters of the model.
Repealing this assumption results in the loss of essential properties of the estimators.
Assumption 3. Matrix row 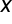is equal to the number of estimated parameters, i.e .
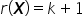The row of the matrix is the number of linearly independent columns. You can also say it’s the number of linearly independent rows. However, in the matrix notation, rows – reflect successive observations, while columns – successive explanatory variables 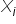. Therefore, it is about independence between the explanatory variables.
These assumptions ensure that the estimator can be determined uniquely.
Assumption 3 implies assumption 4 and assumption 5. Therefore, listing these assumptions separately is sometimes omitted.
Assumption 4. The sample size is larger than the number of estimated parameters, i.e. .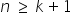
The number of observations n should be greater than the number of estimated parameters (explanatory variables).
Assumption 5. There is no phenomenon of collinearity between explanatory variables
The explanatory variables cannot be collinear. observation vectors of explanatory variables (columns
matrix X) should be linearly independent.
The random component has its own specific properties that should be met under the assumption.
The formation of the random component in econometric model in its general form is one of the basic sources of knowledge about whether the model has been built correctly.
Its value is the difference between the empirical value in a given period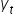 and the estimated theoretical value for the values of explanatory variables in a given period.
By definition a model (in a broad sense) is a simplified picture of reality. In this case, when building an econometric model, we want to “simplify” certain phenomena occurring in economics, to the form of a function. At the same time, we expect that the model will reflect reality as best as possible, thus the difference between the value that occurred in reality (empirical) and what we calculated on the basis of the model (theoretical) will be as small as possible, i.e. as close to zero as possible.
The properties of the random component are listed below. Although they sound complicated, it is easier than it sounds.
Let’s start with the fact that if the random component was shaped according to some pattern, then we could hardly talk about any randomness. For us, this would only mean that “something is going on” in this rest, and the model was not built correctly. If we see that something is going on, we should find out what is hidden there. Most likely, in the values of the random component, in the case of its autocorrelation, there is a factor that has a significant impact on the formation of the dependent variable. A factor that we did not take into account when considering what may affect the issue we are investigating. One of the quick methods aimed at the expected decrease in the autocorrelation coefficient is to add an endogenous variable lagged in time to the model, but more on that later because it is a much more complicated matter.
Assumption 6. The expected value of the random term is zero: .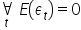
The expected values of the random components are equal to zero ( 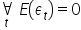for t=1,2,…,n). This means that the disturbances represented by the random components tend to reduce each other.
Assumption 7. The random component has a constant finite variance .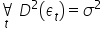
Random component variances 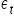are constant, i.e. 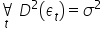for t=1,2,…,n. This is the so-called homoscedasticity property.
The matrix of variance and covariance between residual terms is of the form
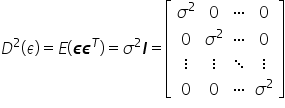
This assumption ensures that the value of the disturbance variance does not depend on the number of observations.
Assumptions 6 and 7 determine the favorable properties of the estimator 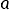parameter vector 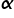but more on that in the next lecture.
Assumption 8. There is no phenomenon of autocorrelation of the random component, i.e. dependence of the random component in different time units .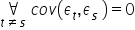
Random components 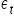and 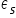they are independent of each other. There is no so-called autocorrelation of random components.
This means a linear relationship between model residuals that are “k” periods apart. This applies to dynamic models.
Its occurrence means that one of the significant explanatory variables has been omitted in the model or an incorrect form of the model has been adopted .
Assumption 9. Random component has n -dimensional normal distribution: 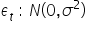For t=1,2,…,n.
Each of the random ingredients has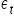 has a normal distribution.
This assumption concerning the normality of the distribution of the random component is important in statistical inference.
If all the above four assumptions in the case of the model we are analyzing turn out to be true, then we can understand the disturbing components as generated by the white noise process . In this case, all autocorrelation coefficients and partial autocorrelation coefficients will be zero, statistically insignificant. To determine if there is white noise, we need to test the relevant hypotheses. These include, for example, Quenouille statistics or Durbin-Watson statistics.
In the above Lecture I tried to bring you closer to the assumptions of the Classical Method of Least squares.
This lecture should actually be preceded by a lecture on the Method of Least Squares, because first the assumptions should be made, then the application of the method and deriving formulas for parameter estimators 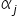model.
I hope that since you already know what the Least Squares Method is and you have learned the assumptions of the applicability of this method, then linear regression will be closer to you and not so scary 🙂
END
Click to revisit what regression and Least Squares are all about and where the formulas for estimating structural parameters come from (previous Lecture)< –
Click here to return to the Econometrics Lectures page
in the model
.
are non-random quantities with fixed elements.
is equal to the number of estimated parameters, i.e 
.
.
.
;
.
For t=1,2,…,n.
and 
result from assumption no 
so they may have been omitted. Often, the last four random components are combined into one sub-clause.
. That is, both parameters and variables should be in prime powers at the same time, and the dependent variable Y should be a linear combination of explanatory variables and various parameters.
is a vector of random components (individual observations) representing the combined effect of all secondary, random factors not included among the explanatory variables. Addition to the deterministic component of the random disturbance vector
and the estimated theoretical value for the values of explanatory variables in a given period.
are constant, i.e. 
parameter vector 
they are independent of each other. There is no so-called autocorrelation of random components.
