Solving systems of equations using the inverse matrix method

In this article, I will introduce a method for solving systems of linear equations, called the “inverse matrix method”. It can be safely added to the known methods: Cramer, Kronecker-Capelli (this is a proper transition to the Cramer method) and Gauss.

We make a reservation right away that the inverse matrix method can only be used in systems of linear Cramer equations, i.e. those in which:

  1. There are as many equations as there are unknowns
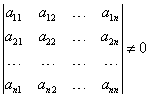
  2. The main determinant of the system (composed of coefficients with variables) is different from zero

1. General case

What is the method? Let’s take a system of equations that satisfies the above assumptions:

System of linear equations

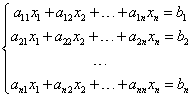
The system has as many equations as it has unknowns (n ​​equations and n unknowns), and its principal determinant is different from zero:

The main determinant of the system

The above system of equations can be written as a multiplication of the following matrices:

System of equations in matrix form

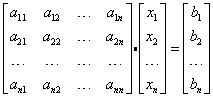
You do not believe? Check for yourself by multiplying the matrices in the appropriate table

The main matrix of the system andMatrix of unknowns :

Matrix multiplication

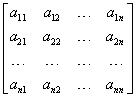
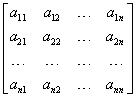
Multiplying the first row by the first (and, of course, only) column, we get:

a_{11} x_{1} +a_{12} x_{2} +...+a_{1n} x_{n} – so exactly the left side of the first equation, which should be equal to b_{1} . This will be the same in the following lines, and you can see that our system of equations and the matrix equation are equivalent. So we go back to the matrix equation:

System of equations in matrix form

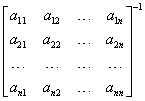
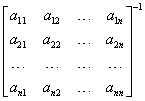
To solve it, we multiply both sides byInverse matrix (inverse matrix) – as it was usually done in matrix equations:

Double-sided multiplication by the inverse matrix

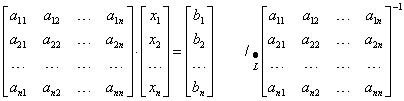
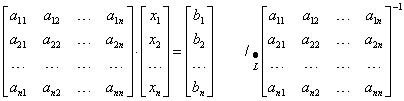
Note that we multiply both sides, but from the left side, because the coefficient matrix is ​​on the left side of the matrix of unknowns. The inverse matrix will exist because its determinant is different from zero, which we ensured in the assumptions (this is the Cramer system). So we go to:

Transformed matrix equation

Now all we have to do is compute the inverse matrix:Inverse matrix ,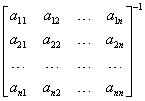
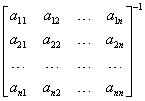
multiply it by the matrix: Matrix of intercepts
…and we get the resulting matrix:
Matrix of unknowns and from there you just need to save the answer 🙂

2. Example

Let’s take a specific system of linear equations:

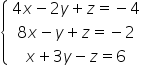
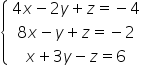
open curly brackets table row cell 4 x minus 2 y plus z equals negative 4 end cell row cell 8 x minus y plus z equals negative 2 end cell row cell x plus 3 y minus z equals 6 end cell end table close

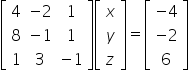
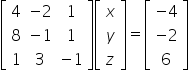
At the beginning we write the matrix form of this system: open square brackets table row 4 cell negative 2 end cell 1 row 8 cell negative 1 end cell 1 row 1 3 cell negative 1 end cell end table close square brackets open square brackets table row x row y row z end table close square brackets equals open square brackets table row cell negative 4 end cell row cell negative 2 end cell row 6 end table close square brackets

Notice that in the first matrix from the left there are the coefficients for the variables of the system, then there is the matrix of unknowns (one-column), and on the right there is the matrix of intercepts. Now it is enough to solve this equation as you solve matrix equations, i.e.:

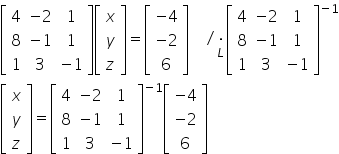
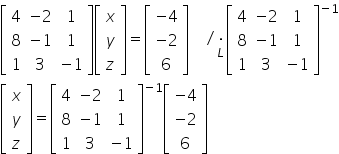
open square brackets table row 4 cell negative 2 end cell 1 row 8 cell negative 1 end cell 1 row 1 3 cell negative 1 end cell end table close square brackets open square brackets table row x row y row z end table close square brackets equals open square brackets table row cell negative 4 end cell row cell negative 2 end cell row 6 end table close square brackets space space space space divided by times for L of open square brackets table row 4 cell negative 2 end cell 1 row 8 cell negative 1 end cell 1 row 1 3 cell negative 1 end cell end table close square brackets to the power of negative 1 end exponent open square brackets table row x row y row z end table close square brackets equals open square brackets table row 4 cell negative 2 end cell 1 row 8 cell negative 1 end cell 1 row 1 3 cell negative 1 end cell end table close square brackets to the power of negative 1 end exponent open square brackets table row cell negative 4 end cell row cell negative 2 end cell row 6 end table close square brackets

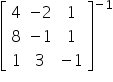
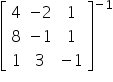
Then compute the inverse matrix: open square brackets table row 4 cell negative 2 end cell 1 row 8 cell negative 1 end cell 1 row 1 3 cell negative 1 end cell end table close square brackets to the power of negative 1 end exponent

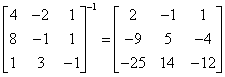
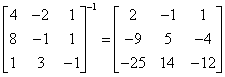
we should get: The result of the inverse matrix

and multiply it by: open square brackets table row cell negative 4 end cell row cell negative 2 end cell row 6 end table close square brackets

…we should then output:

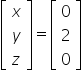
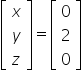
open square brackets table row x row y row z end table close square brackets equals open square brackets table row 0 row 2 row 0 end table close square brackets

Now all that’s left to do is save the answer:

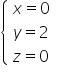
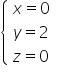
answeropen curly brackets table row cell x equals 0 end cell row cell y equals 2 end cell row cell z equals 0 end cell end table close .

3. Summary

The inverse matrix method has the advantage that you don’t need much new knowledge to learn it other than the ability to calculate inverses and solve matrix equations.

Its disadvantage, however, is the great tediousness of calculations and the limitation to Cramer systems.

Systems of equations that have more than three equations and unknowns require the calculation of inverse matrices larger than 3 \times 3 dimension. This requires the use of a method other than counting from the complement matrix. It is:
Gauss-Jordan Inverse Matrix (next Lecture) –>

Click to recall how to solve systems of linear equations with a parameter (previous Lecture)< —

Click to return to the page with Lectures to the Matrix

Leave a Reply

Your email address will not be published. Required fields are marked *

Your comment will be publicly visible on our website along with the above signature. You can change or delete your comment at any time. The administrator of personal data provided in this form is eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. The principles of data processing and your related rights are described in our Privace Policy (polish).