Matrix rank Lecture 1
Topic: Matrix rank – definition
Summary
In the article, I will simply present what a rank of a matrix is.
Introduction – definition of a vector
Before we get to the matrix itself, let’s talk about what a vector is. We met with vectors in high school and perhaps in college, in the topic of analytic geometry. There they meant a shift on the plane, e.g. 
– it was a vector representing a shift on the OX axis two units to the right, and on the OY axis four units down. Vectors are indicated by arrows. 
– it was a vector in three-dimensional space, and its coordinates mean shifts along the appropriate axes. You can also imagine it as an arrow.
However, if we extend the concept of a vector to more coordinates, we will obtain a single-row matrix, e.g. 
– it is a 9-dimensional vector. It doesn’t have to mean any geometric shift (movement in 9 dimensions? – well…), but, for example, prices in an inflation basket or something.
So let’s forget about vectors as geometric shifts, and let’s agree on a new definition : a vector is a single-row (or single-column, it doesn’t matter) matrix.
Definition of dependent and independent vectors
Once we know what a vector is, we can define when two (let’s start from just two) vectors are linearly dependent from each other. Two vectors are said to be linearly dependent when there exists a constant (number, or ‘scalar’) ‘k’, such that when one of the vectors is multiplied by the constant ‘k’, they are equal, i.e.
\mathop \exists \limits_k \vec x = k\vec yBy the symbol 
we mean a vector, and this strange symbol:
is the inverted letter “e” from the English word “exists”. 
we read: “there exists such k”.
Example of two dependent vectors is:
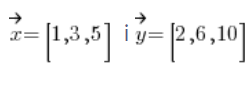, because vector
is vector multiplied by 2.
The geometric interpretation of two two- or three-dimensional linear dependent vectors is their direction, i.e. linear dependent vectors have the same direction and differ only in head/tail or length.
Of course, there is no way that, for example, vectors: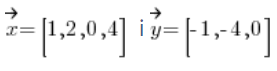
, i.e. vectors representing different dimensions (different parts of elements) were linear. That’s obvious, because multiplying by constant (number, scalar) can’t change vector dimension, right?
However, a linear relationship of vectors can be determined for a larger number of them. We define this as follows:
Definition
Vectors
we are called linearly dependent vectors if there exists such constants [
(at least one of which is non-zero) that:
Conversely, we could say that two vectors are independent if there are NO such constants (at least one of which is non-zero) that:
The geometric linear interpretation of three-dimensional vectors is their “coplanarity”, i.e. they belong to one plane. Three-dimensional linear dependent vectors are coplanar, i.e. belonging to one plane.
Calculating a linear line of vectors
It is not difficult to imagine that the task of the next person to determine whether vectors are linearly functional or regardless of their equivalent is tiring (even tiring equally). For example, for four-dimensional vectors:
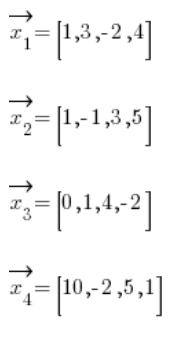
We would need to check whether this condition is permanent
(such that at least one of them is different from zero) that:
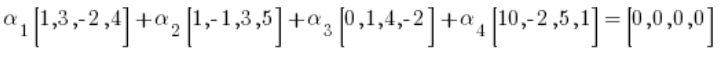
So (after multiplying the vectors by the constant):
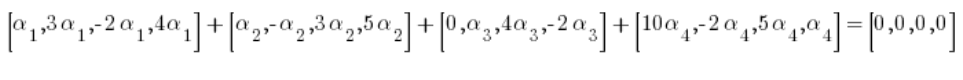
Which is equivalent to the system of equations:
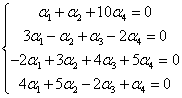Now you need to check or check some solutions to this mechanism because of this error that all are equal to zero.
Long, tedious, inconvenient, right?
Home government
Here we come to what motherhood is. If we arrange the vectors (or in columns – it doesn’t matter) one below the other, we will get the parent vector, right? For example, for our vectors with the example above it would be:
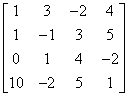
Let’s define the row of the matrix:
Definition
Parent row to the maximum number of linear vector coefficients in the rows (or columns) of this matrix.
Calculating a matrix coefficient is already much, much different than messing with an equal (how to do it exactly, the implementation is for example in my Matrix Course). The interpretation of the origin is simple. If the rank of this matrix after calculation was equal to 3, it means that there are only 3 lines in these vectors that are independent of each other, i.e. these four lines as a whole are linearly independent.
However, it so happens that:
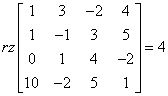
This means that the row of this matrix is four. So we have four vectors, 4 of which are independent. The obvious conclusion is that these vectors are independent .
Click to see how to check blood test for proof check vectors (next Lecture) –>
Click to download to the website with Lectures for the matrix