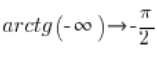Inverse trigonometric functions Lecture
Topic: Inverse trigonometric functions
Summary
During the lecture I will introduce the concept of cyclometric functions: arcsinx (in english notation: {sin}^{-1} {x} ), arccosx (in english notation: {cos}^{-1} {x} ), arctgx (in english notation: {tan}^{-1} {x} ), arcctgx (in english notation: {cot}^{-1} {x} ). These are inverse functions to trigonometric functions.
Let’s stress once again, that in below lecture notation is:
arcsinx is equivalent to {sin}^{-1} {x}
arccosx is equivalent to {cos}^{-1} {x}
arctgx is equivalent to {tan}^{-1} {x}
arcctgx is equivalent to {cot}^{-1} {x}
The lecture consists of two parts. In the first one, I only show how to quickly calculate the values of inverse trigonometric functions, without going too deep into the topic (this part is accompanied by a video, a fragment of my Course on Definite Integrals and Applications of Integrals (in polish) ).
In the second part, I describe inverse trigonometric functions more precisely, show their graphs, etc.
To understand the lecture you will need:
- trigonometric functions (high school)
Part I
Inverse trigonometric functions – “INSTANT” version
Inverse trigonometric functions “in common sense” are simply the opposite of trigonometric functions. So arcsinx (or {sin}^{-1} {x}) is the inverse function of sinx.
That is, if, for example, we know that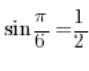 , it means that
, it means that![]() .
.
And so on:
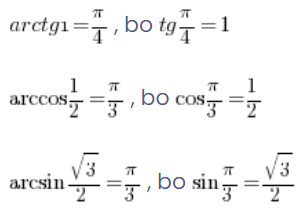
In addition, we have a few properties of inverse trigonometric functions that allow us to calculate their values also for negative arguments:
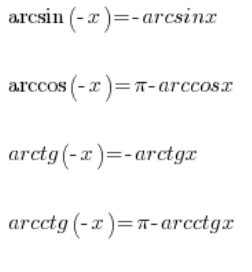
So we can also calculate this:
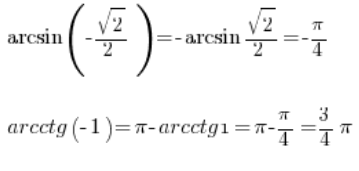
So, if we have a table of values if trigonometric functions, we can easily determine the values of inverse trigonometric functions from it, simply by reading it “the other way around”.
I explain it in more detail here in the video:
Table of basic values of trigonometric functions from the video – download here .
Part II
Inverse trigonometric functions – full version
Introduction – why part one is not enough
So it looks like in Part One we defined each inverse trigonometric function as the inverse of its corresponding trigonometric function.
Let’s formalize this a bit. We said, for example, a function![]() takes a value
takes a value![]() when function
when function![]() from this
from this![]() is equal
is equal![]() .
.
Appropriately:
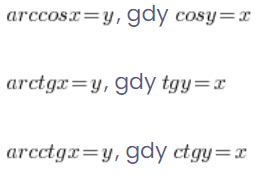
That is, if we want to calculate![]() we wonder what the cosine of the angle gives
we wonder what the cosine of the angle gives![]() , we realize that it is an angle
, we realize that it is an angle![]() and we have the result:
and we have the result: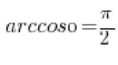 .
.
Does this exhaust the topic of the values of inverse trigonometric functions?
Of course NO .
Let’s look at the whole reasoning again using specific numbers:
If we want to calculate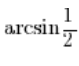 we wonder what the sine of the angle gives
we wonder what the sine of the angle gives![]() , we realize that it is an angle
, we realize that it is an angle![]() and we have the result:
and we have the result: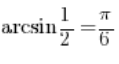 .
.
Where’s the problem? In the bolded part:
If we want to calculate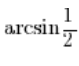 we wonder what the sine of the angle gives
we wonder what the sine of the angle gives![]() , we realize that it is an angle
, we realize that it is an angle![]() and we have the result:
and we have the result: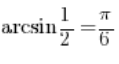 .
.
Unfortunately, not only sine![]() is equal to
is equal to ![]() .
.
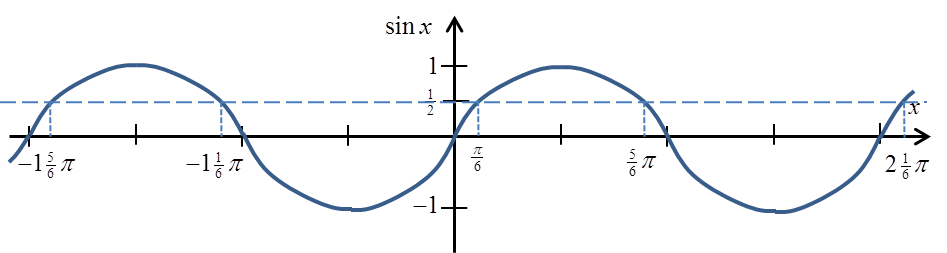
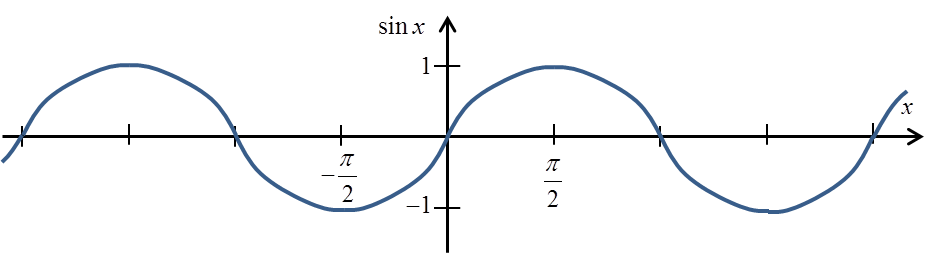
Let’s recall the graph of the sinx function (I marked the value ![]() on it):
on it):
You can see and we already know it from high school that the sine reaches a value![]() not just for the angle
not just for the angle![]() , but also for angles:
, but also for angles: 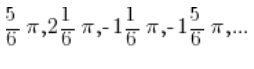
That is 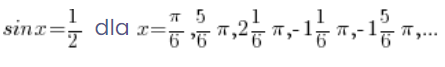
So let’s recall once again our way of calculating arcsin:
If we want to calculate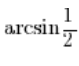 we wonder what the sine of the angle gives
we wonder what the sine of the angle gives![]() , we realize that it is an angle
, we realize that it is an angle![]() and we have the result:
and we have the result: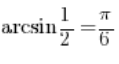 .
.
Well, now we know that it’s not just sin![]() gives
gives ![]() , so it looks like:
, so it looks like:
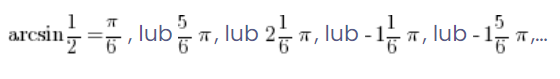
This would mean actually, that arcsinx ({sin}^{-1} {x}) is not a function at all, because one argument has several values assigned to it!
Giving a clear answer to the question of what the arcsin ({sin}^{-1}) of something is equal exactly would then be completely impossible.
It is also easy to imagine that a similar problem applies to EACH trigonometric function.
To put it more professionally: these functions are not one-valued, so inverse functions do not exist. In each of the trigonometric functions, each of their values is reached for an infinite number of arguments (they are periodic, right?), so when we try to determine their inverse functions, we will get an infinite number of values assigned to each argument. And this cannot be the case in functions.
What to do?
It’s quite simple, not to mention vulgar. Each trigonometric function can be TRUNCATED to obtain a one-valued function.
Let’s get started, let’s define all 4 inverse trigonometric functions correctly:
arcsinx ({sin}^{-1} {x})
Let us recall the graph of the sinx function:
If we agree to cut it, for example, to a compartment![]() , we will get a chart like this:
, we will get a chart like this:
![Sinx plot in the interval [0,pi] Image3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
Unfortunately, this is not what we want, because there is no graph of a one-valued function and a problem with the value, e.g. ![]() still occurs:
still occurs:
![Graph of the sinx function in the interval [0,pi] with the value 1/2 marked Graph of the sinx function in the interval [0,pi] with the value 1/2 marked](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
So we agree that we will trim the sinx function differently, to the arguments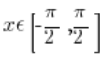 : :
: :
![Graph of the sinx function for x belonging to [-pi/2,pi/2] Graph of the sinx function for x belonging to [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
Now it is a one-valued function and there is an inverse arcsinx ({sin}^{-1} {x}) function to it.
The graph of the arcsinx ({sin}^{-1} {x}) function will look something like this:

Its domain is the interval![]() does not exist.
does not exist.
The precise definition of the arcsinx ({sin}^{-1} {x}) function is therefore:
![]() .
.
arccosx ({cos}^{-1} {x})
The cosx function is also not a single-valued function:
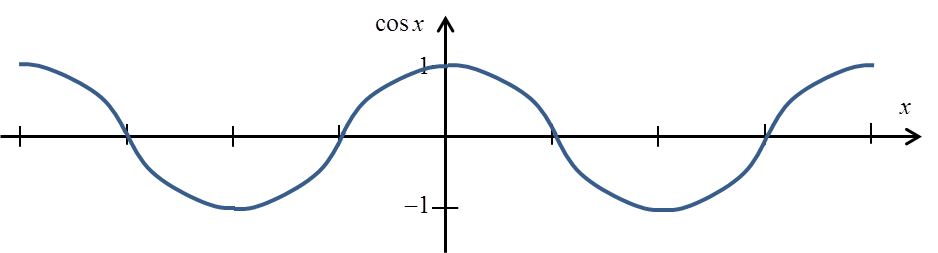
However, to obtain a one-valued function, we must trim it to an interval![]() :
:
![Graph of the cosx function truncated to the interval [0,pi] Graph of the cosx function truncated to the interval [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
The function defined in this way is already single-valued and has the inverse function arccosx ({cos}^{-1} {x}).
Its graph will be approximately:
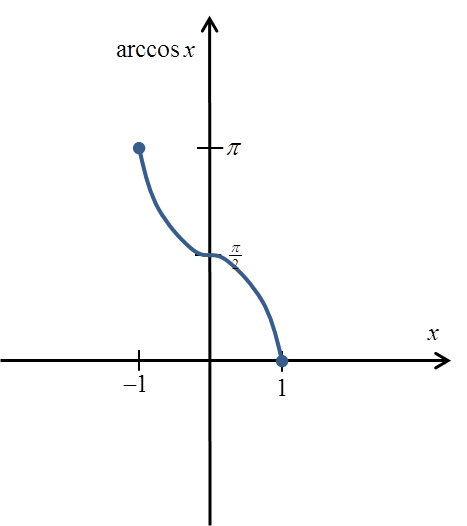
And its strict definition:
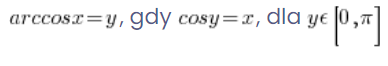 .
.
arctgx ({tan}^{-1} {x})
The tgx function graph looks like this:

It’s also not a single-valued function! We can cut it as follows:
![Graph of the tgx function limited to the range [-pi/2,pi/2] Graph of the tgx function limited to the range [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
Thus obtaining a single-valued function.
The arctgx ({tan}^{-1} {x}) function graph looks like this:

And its precise definition is as follows:
![]() , for y\in \left( -\frac{\pi }{2} ,\frac{\pi }{2} \right) .
, for y\in \left( -\frac{\pi }{2} ,\frac{\pi }{2} \right) .
Let’s also note that the graph shows some interesting properties, e.g.:
- the domain of the arctgx ({tan}^{-1} {x}) function is the entire set of real numbers (we can calculate arctg from each number)


arcctgx ({cot}^{-1} {x})
From the ctgx function graph:

We cut out a multi-valued piece:
The arcctgx ({cot}^{-1} {x}) function graph looks like this:
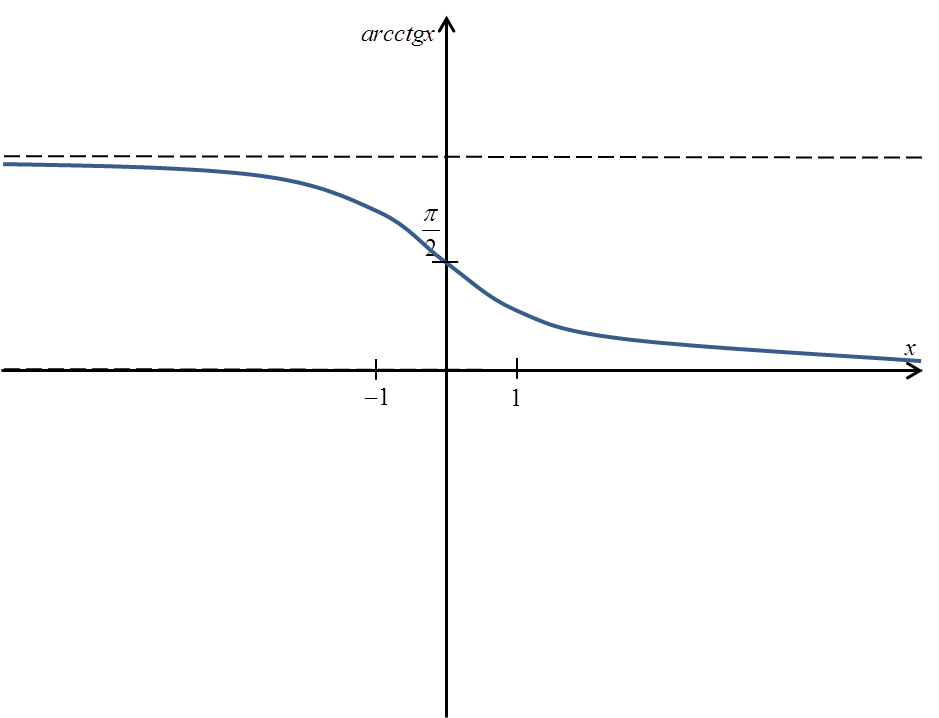
A precise definition of arcctgx ({cot}^{-1} {x}) would be:
![]() .
.
It seems:
- the domain of the arcctgx ({cot}^{-1} {x}) function is the entire set of real numbers (we can calculate arcctg ({cot}^{-1} {x}) from each number)


Attention
In many calculators and mathematical notations in general (especially Western ones), inverse trigonometric functions are not marked as “arcus”, but with an exponent of -1. For example, arcsinx is written as![]() . If you know what you’re talking about, there’s no problem. However, you can make a terrible mistake and confuse the inverse of sinx with a function
. If you know what you’re talking about, there’s no problem. However, you can make a terrible mistake and confuse the inverse of sinx with a function![]() – which is a completely different function from arcsinx.
– which is a completely different function from arcsinx.