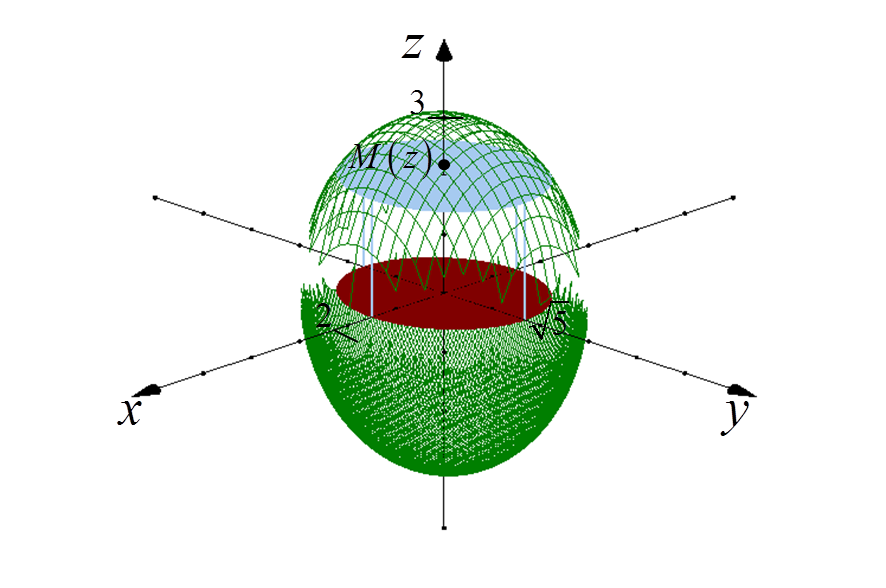
The Volume of an Ellipsoid (But Not a Rotational One, Just a Wild Type) Calculated by a Definite Integral
Let’s say we need to calculate the volume of an ellipsoid: {x^2}/4+{y^2}/5+{z^2}/9=1. This is an ellipsoid that intersects the x, y, z axes at coordinates 2, \sqrt{5}, and 3, respectively.
This is not a rotational ellipsoid, it is not formed by rotating any curve around any axis, so we can’t use the standard formula for the volume of a rotational solid. We need to figure out another way.




