When calculating square roots in Cartesian (or: algebraic) form in my Complex Numbers Course, I showed a method that involves adding a third equation to the existing system of two equations, which greatly simplifies and shortens the further calculations.
I showed this method, but didn’t justify it in any way.
Recently, I received an email regarding this:
Hello
Could you explain why we can use the method of adding a third equation when calculating the square root of a complex number?
x^2 + y^2 = the modulus of the number we are calculating the root of
This is a VERY good question and really blessed in mathematics are those who don’t just believe professors but always ask: “Where did this come from?” 🙂
Justification
So, there’s nothing left but to justify this method in one of the possible ways:
After the first few steps in calculating the square root, we have the situation:
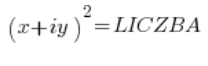
Since the numbers (I won’t keep writing “complex numbers” each time) on the left and right are equal, their moduli must also be equal (it doesn’t work the other way around, but that’s not important), that is:
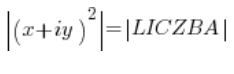
A number squared is a number times itself, that is:
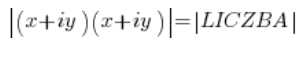
The modulus of a complex number has the property: ![]() , so on the left side we can write:
, so on the left side we can write:
![]()
… and calculating the moduli on the left we have:
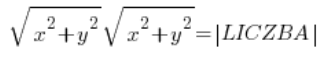
that is:
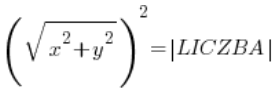
that is:
![]()
that is:
BINGO
Thanks for the great question!


