To answer the question posed in the title, we don’t need to go back to the definition of an oblique asymptote, we just need to know what a function is.
As is often the case in mathematics, let’s imagine that the graph of the function HAS two different oblique asymptotes at ![]() , and show that assuming this will definitely lead us to a contradiction, so this assumption cannot be accepted.
, and show that assuming this will definitely lead us to a contradiction, so this assumption cannot be accepted.
Graph
In the graph, these asymptotes might look like this:
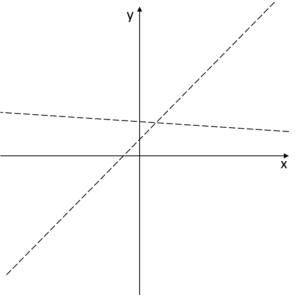 And the graph of the function should approach these asymptotes at
And the graph of the function should approach these asymptotes at ![]() , so it will look like this:
, so it will look like this:
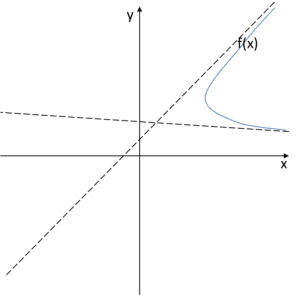 And what? Can it be like this? Can the graph of a function look like this? Or do we have a problem here?
And what? Can it be like this? Can the graph of a function look like this? Or do we have a problem here?
Problem
Of course, we have a problem. What is shown above cannot be the graph of a function. Let’s go back to the basics, a function by definition is a mapping that assigns exactly one y value to each x argument. And what does our graph show?
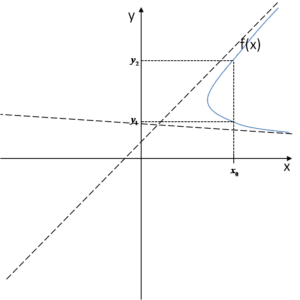 We can see that, for example, the argument
We can see that, for example, the argument ![]() is assigned two values –
is assigned two values – ![]() and
and ![]() . And that can’t happen in a function graph, because each x argument must correspond to only one y value.
. And that can’t happen in a function graph, because each x argument must correspond to only one y value.
Therefore, a function cannot have two different oblique asymptotes at ![]() . The entire reasoning can be repeated accordingly for
. The entire reasoning can be repeated accordingly for ![]() 🙂
🙂


