When tackling problems using complex polynomial equations, we generally employ the same methods as we do for solving real polynomial equations in high school.
Fourth Degree Complex Equations Reducible to Second Degree
This also applies to fourth degree complex equations that can be reduced to second degree ones, meaning those where we have variables to the fourth power, to the second power, and a constant term, for example:
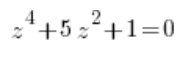
or:
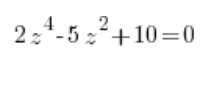
We reduce these types of complex equations to second degree complex equations by substituting 
, where 
is obviously the complex variable.
Task
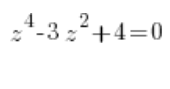
We substitute (of course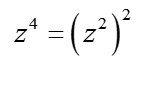 
), thus we get:
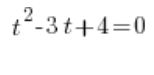
And thus we solve this equation in the usual way using the discriminant (of course, roots of negative numbers exist in complex numbers). We will obtain two complex solutions:
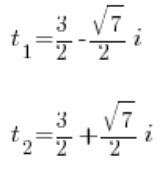
Since we substituted: , we have:
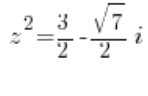
or:
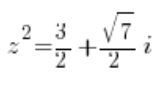
That is:
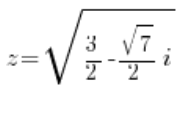
or:
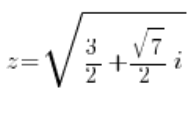
After calculating the roots (of course, there will be four complex roots), we will have four solutions:
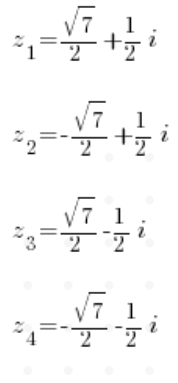
P.S. I show this and other methods in Lesson 6 of my Complex Numbers Course, check it out!
