Ekonometria Wykład 6
Temat: Analiza regresji. Szacowanie parametrów modelu
Metodą Najmniejszych Kwadratów.
W tym Wykładzie przedstawię Ci na czym polega regresja liniowa oraz jak dokładnie działa Metoda Najmniejszych Kwadratów. Dowiesz się zatem skąd wzięły się wzorki na oszacowania parametrów strukturalnych 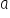 modelu ekonometrycznego.
modelu ekonometrycznego.
Zapraszam!
Główny cel ekonometrii to zbadanie i wyjaśnienie zachowania jednej zmiennej ekonomicznej w zależności od zachowania innych zmiennych. Oczywiście muszą być one ze sobą w jakiś sposób powiązane. Np.: czy i w jaki sposób wydatki rodziny zależą od jej dochodu?; – czy wzrost wydatków na żywność jest szybszy, czy wolniejszy w zależności od wzrostu dochodu?
W jednym z poprzednich Wykładów przedstawiłam temat o zależności statystycznej, jaką jest korelacja. Jak pamiętamy, pojęcie korelacji dotyczy SIŁY i KIERUNKU badanej współzależności.
Oprócz analizy korelacji, można dokonać jeszcze innego typu analizy – tzw. REGRESJI. Jest ona działem statystyki zajmującej się badaniem związków i zależności pomiędzy rozkładami dwu lub więcej badanych cech w populacji generalnej.
Termin regresja dotyczy jednak KSZTAŁTU zależności pomiędzy cechami. Dzieli się na analizę regresji liniowej i nieliniowej.
Wykresem regresji liniowej dwóch zmiennych, jak sama nazwa wskazuje, będzie prosta. W przypadku analizy regresji nieliniowej, graficzną reprezentacją współzależności są krzywe wyższego rzędu np. parabola.
Wystarczy spojrzeć na poniższe chmury punktów. na ich podstawie można stwierdzić, że im wartości współczynnika korelacji są bliższe 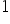 (w module), tym bardziej punkty na wykresie układają się w sposób liniowy. W trzecim wierszu zaprezentowano przykłady wykresów nieliniowych.
(w module), tym bardziej punkty na wykresie układają się w sposób liniowy. W trzecim wierszu zaprezentowano przykłady wykresów nieliniowych.
Źródło: https://pl.wikipedia.org/wiki/Zależność_zmiennych_losowych, dn. 12.06.2018 r.
Analiza regresji i korelacji może dotyczyć nie tylko dwóch, ale również i większej ilości zmiennych. Mówimy wtedy o tzw. analizie wielorakiej.
Przejdę teraz do omówienia zarówno jednego, jak i drugiego przypadku regresji liniowej.
Regresja liniowa – wstępne informacje
Nazwa regresja liniowa wywodzi się od tego, że zakładanym modelem zależności między zmiennymi zależnymi a niezależnymi jest funkcja liniowa bądź przekształcenie liniowe.
Prostą, którą wyznacza równanie modelu liniowego jest prosta regresji, zaś model – modelem regresji liniowej. O prostej regresji można mówić jedynie w przypadku modelu ze stałą i jedną zmienną objaśniającą. W przypadku wielowymiarowym, czyli regresji wielorakiej, mówimy o hiperpłaszczyźnie regresji.
Zanim pojawią się bardziej szczegółowe wykresy, warto przypomnieć ogólną postać modelu ekonometrycznego:
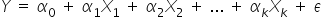
Uwzględniając realizacje zmiennych często zapisuje się go następująco:
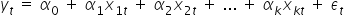
przy czym:
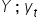 – zmienna objaśniana, zależna, endogeniczna; realizacje zmiennej objaśnianej w okresie t,
– zmienna objaśniana, zależna, endogeniczna; realizacje zmiennej objaśnianej w okresie t,
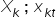 – zmienne objaśniające, niezależne; realizacje zmiennych objaśniających w okresie t,
– zmienne objaśniające, niezależne; realizacje zmiennych objaśniających w okresie t,
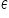 – składnik losowy (więcej o nim poczytasz w artykule),
– składnik losowy (więcej o nim poczytasz w artykule),
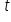 – kolejne realizacje (obserwacje),
– kolejne realizacje (obserwacje), 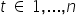 .
.
Interesująca jest sama geneza terminu regresja.
W mowie potocznej regresja oznacza: cofanie się, spadek, zanik. Możesz zatem się zastanawiać, skąd wzięło się ono w statystyce?
Termin ten jako pierwszy użył Francis Galton, zięć Karola Darwina. W 1886 roku badał on związek pomiędzy wzrostem rodziców i ich dzieci. Zauważył, że wysocy rodzice mają też średnio wysokie dzieci. Jednakże wzrost dzieci ponadprzeciętnie wysokich rodziców jest bliższy średniej, niż wzrostowi ich rodziców. Taką tendencję powrotu do średniej Galton określił jako: „regresję do średniactwa”. Jego wioski można więc zapisać za pomocą następującego modelu liniowego:
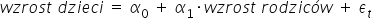
gdzie wartość parametru stojącego przy zmiennej objaśniającej zawiera się pomiędzy 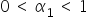 . Wynika stąd, że centymetr wzrostu rodziców przekłada się na mniej niż jeden centymetr wzrostu dzieci.
. Wynika stąd, że centymetr wzrostu rodziców przekłada się na mniej niż jeden centymetr wzrostu dzieci.
Zmienna objaśniana i zmienne objaśniające w modelu regresji nie są symetryczne. Galton w swoich badaniach nie tylko zakładał to, że wzrost rodziców ma wpływ na wzrost dzieci, ale i to, że odwrotnie skutek ten nie działa, tzn. wzrost rodziców nie zależy od wzrostu dzieci.
Należy zatem zauważyć, że w teorii ekonomii bardzo ważnym jest znajomość kierunku związku przyczynowo-skutkowego.
Regresja liniowa prosta
Regresja liniowa prosta dotyczy przypadku dwóch zmiennych – objaśnianej Y i jednej objaśniającej X.
Prostą można opisać znanym Ci (jeszcze z gimnazjum) wzorem: 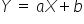 . Ten zapis jest najprostszy. Jeśli zatem wiemy już co oznaczają literki Y i X, to pozostałe dwie oznaczają:
. Ten zapis jest najprostszy. Jeśli zatem wiemy już co oznaczają literki Y i X, to pozostałe dwie oznaczają:
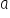 – parametr stojący przy zmiennej, jest to współczynnik kierunkowy regresji, tangens kąta
– parametr stojący przy zmiennej, jest to współczynnik kierunkowy regresji, tangens kąta 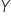 nachylenia prostej do osi OX,
nachylenia prostej do osi OX,
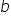 – wyraz wolny (stała), współrzędna punktu przecięcia z osią OY.
– wyraz wolny (stała), współrzędna punktu przecięcia z osią OY.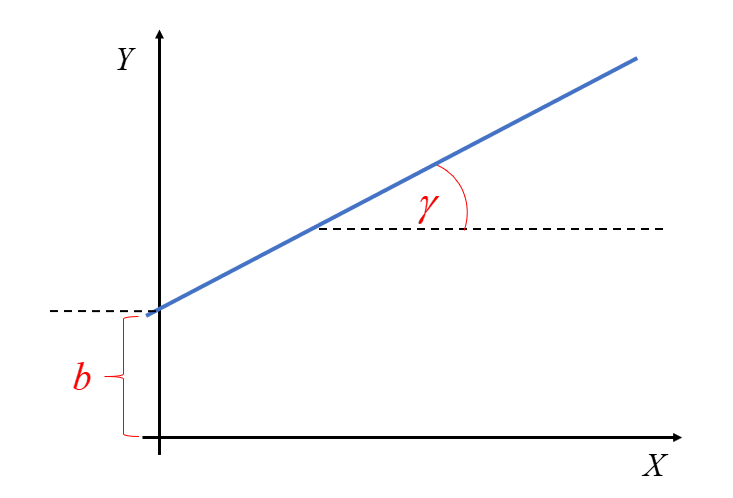
Większość z osób zapewne pamięta, jak w szkole średniej czy gimnazjum znajdywało się prostą przechodzącą przez dwa punkty 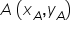 oraz
oraz 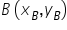 . Oczywiście był na to konkretny wzór, dostępny np w tablicach maturalnych:
. Oczywiście był na to konkretny wzór, dostępny np w tablicach maturalnych: 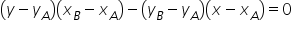 . Równie dobrze wystarczyło rozwiązać układ równań dwóch prostych, podstawiając za X i Y współrzędne punktów, typu
. Równie dobrze wystarczyło rozwiązać układ równań dwóch prostych, podstawiając za X i Y współrzędne punktów, typu 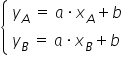 i z tego wyliczyć nieznane wartości parametrów
i z tego wyliczyć nieznane wartości parametrów 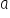 i
i 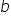 .
.
Warto pamiętać, że w ekonometrii NIE mamy jednak do czynienia ze związkiem funkcyjnym (zwanym często deterministycznym), czyli takim, w którym każdej wartości 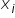 odpowiada jedna i tylko jedna wartość
odpowiada jedna i tylko jedna wartość 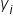 .
.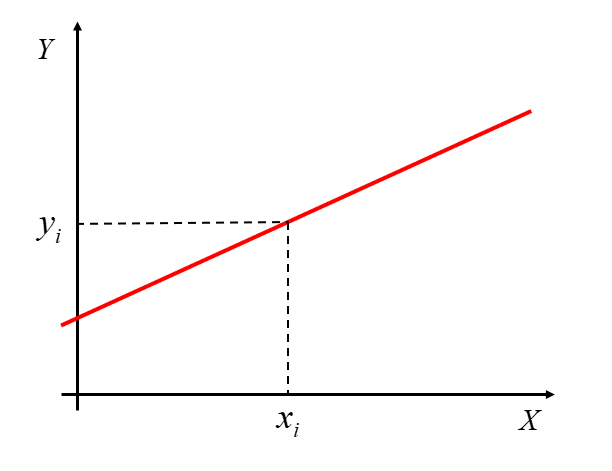
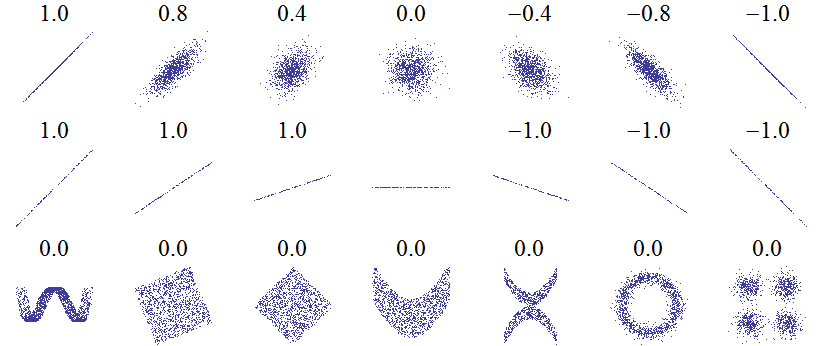
W ekonometrii bada się związki stochastyczne (losowe, probabilistyczne) pomiędzy zmiennymi X i Y. W tym przypadku KAŻDEJ wartości 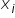 odpowiada cały zbiór wartości
odpowiada cały zbiór wartości 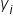 tworzących określony rozkład. Stąd typowe równanie linii regresji prostej jest następujące:
tworzących określony rozkład. Stąd typowe równanie linii regresji prostej jest następujące:
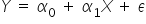
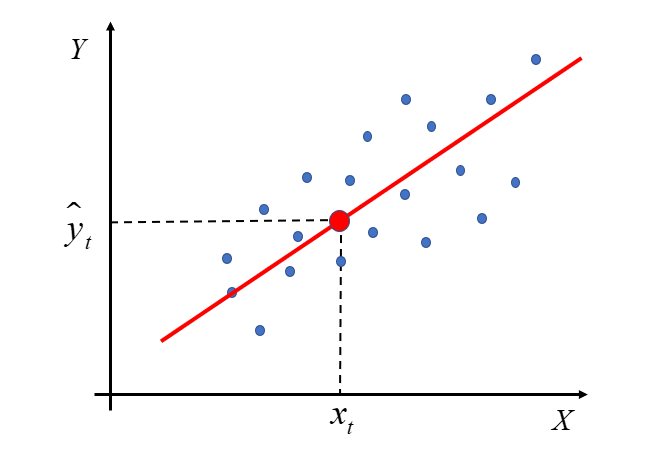
Sytuację taką można zobrazować następująco:
Jeżeli rozkład ten jest rozkładem normalnym (jeden z typów rozkładów statystycznych zmiennych losowych), to zależność Y(X) jest liniowa.
Przejdźmy zatem do meritum. Otóż narysowanie prostej przechodzącej przez dwa punkty wydaje się sprawą łatwą. Niemniej jednak, w przypadku wielu punktów nie pójdzie już tak łatwo. Praktycznie nigdy nie zdarzy się sytuacja, kiedy prosta przeszłaby przez każdy z zaznaczonych na wykresie elementów.
W tym przypadku, należy wybrać taką metodę, która pozwoli znaleźć najbardziej optymalną prostą. Powinna ona być odpowiednio „dopasowana”, tj. być narysowana tak, aby jak najlepiej zobrazować zależność pomiędzy X i Y.
Taką prostą (czyli równanie regresji, w postaci TEORETYCZNEJ) zapisuje się jako:
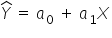
Uwzględniając konkretne realizacje zmiennych, w kolejnych okresach t, można ją również zapisać:
W tym przypadku, 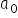 – jest to estymator, czyli oszacowana wartość wyrazu wolnego. Natomiast
– jest to estymator, czyli oszacowana wartość wyrazu wolnego. Natomiast 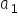 reprezentuje oszacowaną wartość współczynnika regresji. Określa ona wpływ zmiennej X na zmienną Y.
reprezentuje oszacowaną wartość współczynnika regresji. Określa ona wpływ zmiennej X na zmienną Y.
Pytanie brzmi – jak wyrazić liczbowo wartości parametrów 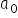 oraz
oraz 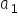 ? Będę miła do narysowania prostą np.
? Będę miła do narysowania prostą np. 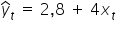 , czy też prostą o lekko innym nachyleniu, np.
, czy też prostą o lekko innym nachyleniu, np. 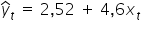 ?
?
W dalszej części wykładu postaram się wyjaśnić matematycznie sposób wyprowadzenia wzorów na najlepsze oszacowania wartości 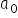 oraz
oraz 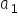 , a także pozostałe parametry
, a także pozostałe parametry 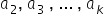 dla przypadku modelu z wieloma zmiennymi objaśniającymi.
dla przypadku modelu z wieloma zmiennymi objaśniającymi.
Estymacja parametrów modelu ekonometrycznego Metodą Najmniejszych Kwadratów – przypadek z jedną zmienną objaśniającą.
Metod oszacowania parametrów modelu jest bardzo dużo. Być może słyszałeś już o metodzie największej wiarygodności, metodzie regresji medianowej czy metodzie dwupunktowej. Niemniej jednak, spośród tych wszystkich metod najpopularniejsza jest Metoda Najmniejszych Kwadratów (w skrócie MNK).
Wymaga ona pewnych założeń, które omówię dokładniej w kolejnym wykładzie. Do najważniejszych z nich należą własności składnika losowego 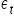 w modelu
w modelu 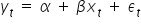 :
:
- wartość oczekiwana składnika losowego jest równa zero
 ;
; - składnik losowy ma stałą skończoną wariancję
 ;
; - nie występuje zjawisko autokorelacji składnika losowego, czyli zależności składnika losowego w różnych jednostkach czasu
 .
.
W ramach ścisłości oznaczeń, w powyższym artykule oraz w całym moim Kursie używam następujących oznaczeń (literek): 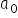 oraz
oraz 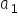 . Są to estymatory metody najmniejszych kwadratów parametrów
. Są to estymatory metody najmniejszych kwadratów parametrów 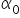 oraz
oraz 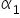 z modelu postaci:
z modelu postaci: 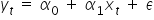 .
.
Na swoich zajęciach być może używałeś modelu postaci ogólnej takiej: 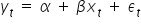 . Zatem szukaliście oszacowań parametrów modelu w postaci teoretycznej:
. Zatem szukaliście oszacowań parametrów modelu w postaci teoretycznej: 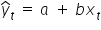 .
.
W literaturze czy na zajęciach, można niejednokrotnie spotkać również i odwrotne oznaczenia modelu: 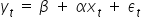 , stąd równanie teoretyczne prostej będzie miało postać:
, stąd równanie teoretyczne prostej będzie miało postać: 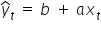 .
.
Najważniejsze jednak jest to, aby zrozumieć, która literka w równaniu oznacza wyraz wolny, a która współczynnik kierunkowy (stojący przy zmiennej X).
W tym miejscu, powróć na chwilę do zamieszczonego wcześniej wykresu. Tak jak wspominałam, poprowadzona czerwona linia nie pokrywa idealnie wszystkich niebieskich punktów. Niektóre z nich leżą poniżej, niektóre powyżej prostej.
Model ekonometryczny będzie tym lepiej dopasowany, im mniejsza będzie odległość wartości teoretycznych 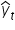 od wartości zaobserwowanych
od wartości zaobserwowanych 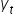 .
.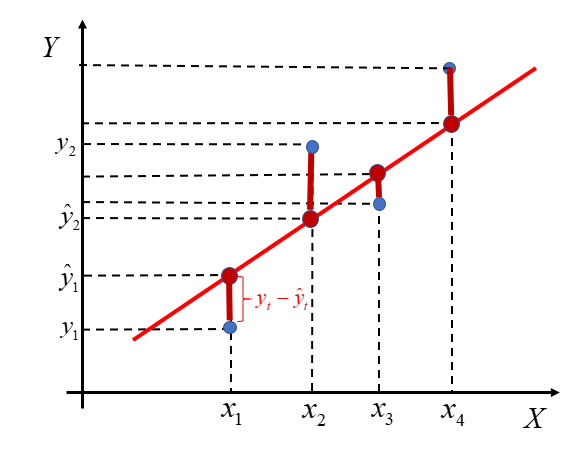
Każdy z tych pionowych (bordowych) słupków reprezentuje różnice pomiędzy wartościami rzeczywistymi zmiennej 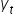 a wartościami teoretycznymi
a wartościami teoretycznymi 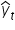 wyliczonymi z linii regresji. Są to tzw. reszty modelu. Oznaczamy je jako:
wyliczonymi z linii regresji. Są to tzw. reszty modelu. Oznaczamy je jako:
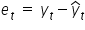
Relację między resztami, obserwacjami i oszacowaniami parametrów, można zapisać następująco:
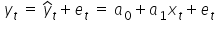
Z tego wynika, że reszty 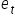 stanowią oszacowania elementów losowych
stanowią oszacowania elementów losowych 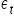 z modelu
z modelu 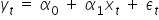 , ale nie są im równe!
, ale nie są im równe!
Niektóre różnice pomiędzy wartościami rzeczywistymi, a teoretycznymi, są powyżej osi, a zatem będą miały wartość dodatnią. Inne są pod osią, stąd będą miały wynik ujemny. Jeśli więc dążymy do tego, aby te odcinki były JAK NAJMNIEJSZE, nie ma sensu dodawać samych różnic 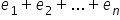 . W takim przypadku wynik nie byłby miarodajny. Dopasowanie będzie tym lepsze, im mniejsze są wartości bezwzględne tych odchyleń.
. W takim przypadku wynik nie byłby miarodajny. Dopasowanie będzie tym lepsze, im mniejsze są wartości bezwzględne tych odchyleń.
Przykład 1
W pewnym modelu różnice pomiędzy wartościami teoretycznymi, a rzeczywistymi wynoszą: 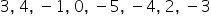 . Są to odległości pomiędzy dwoma punktami. Można je porównać np. do temperatury na termometrze i odległości od zera – raz jest dodatnia, raz ujemna. Lub też do zrobionych kroków do przodu (te na plusie) i do tyłu (te na minusie).
. Są to odległości pomiędzy dwoma punktami. Można je porównać np. do temperatury na termometrze i odległości od zera – raz jest dodatnia, raz ujemna. Lub też do zrobionych kroków do przodu (te na plusie) i do tyłu (te na minusie).
Jeśli potrzebujesz policzyć całościową różnicę, czyli łączne dodanie wszystkich odległości, to zwykła suma liczb nie będzie miarodajna: 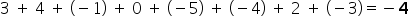 . Wiele liczb się po prostu skróciło. Nie zrobiłeś przecież tylko czterech kroków do tyłu. Dlatego do sumy wykorzystać należy wartość bezwzględną danej liczby, czyli jej odległość na osi od zera. To jakbyś policzył kroki – te do przodu i te do tyłu, ale łącznie.
. Wiele liczb się po prostu skróciło. Nie zrobiłeś przecież tylko czterech kroków do tyłu. Dlatego do sumy wykorzystać należy wartość bezwzględną danej liczby, czyli jej odległość na osi od zera. To jakbyś policzył kroki – te do przodu i te do tyłu, ale łącznie.
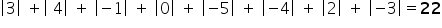 Teraz się wszystko zgadza 🙂
Teraz się wszystko zgadza 🙂
Kryterium, które należy zminimalizować, aby uzyskać najlepsze dopasowanie, jest sumą wszystkich reszt co do wartości bezwzględnej:
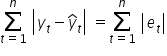
Aby znaleźć wartości najmniejsze, czyli tzw. ekstrema lokalne funkcji wielu zmiennych potrzebne są pochodne (więcej na ich temat odnajdziesz w Kursach Pana Krystiana).
Funkcja ta jest jednak kłopotliwa w użyciu, ponieważ dla modułu nie istnieje pochodna funkcji w zerze. W rezultacie nie da się zminimalizować sumy 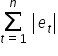 standardowymi metodami analitycznymi.
standardowymi metodami analitycznymi.
Z pomocą przychodzi Metoda Najmniejszych Kwadratów. Jak sama nazwa wskazuje, pozwala ona szukać minimum dla sumy kwadratów różnic wartości obserwowanych i wartości teoretycznych (obliczonych z równania modelu).
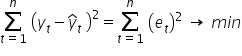
Podstawiając równanie teoretyczne modelu otrzymuję:
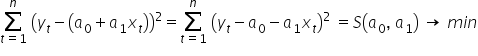
Należy teraz znaleźć minimum funkcji sumy 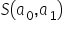 . Czyli dobrać tak oszacowania
. Czyli dobrać tak oszacowania 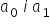 , aby suma ta była jak najmniejsza.
, aby suma ta była jak najmniejsza.
Posługując się analizą matematyczną, można znaleźć ekstremum funkcji. Wystarczy tutaj obliczyć pochodne cząstkowe funkcji względem parametrów i przyrównać je do zera. W przypadku funkcji 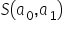 warunki te można zapisać jako układ równań:
warunki te można zapisać jako układ równań:
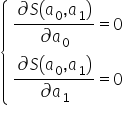
Do policzenia pochodnych cząstkowych, można oczywiście rozpisać wyrażenie w nawiasie podniesione do kwadratu, czyli:
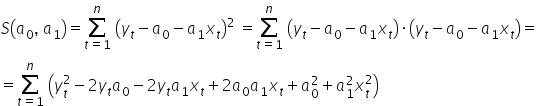
Licząc pochodne cząstkowe i wykorzystując przy tym podstawowe wzory z pochodnych, czyli 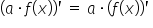 ,
, 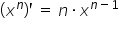 ,
, 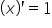 oraz
oraz 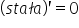 otrzymam:
otrzymam:
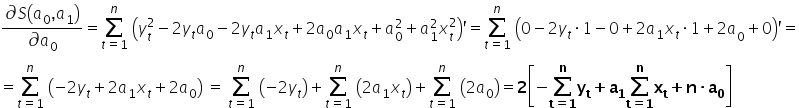
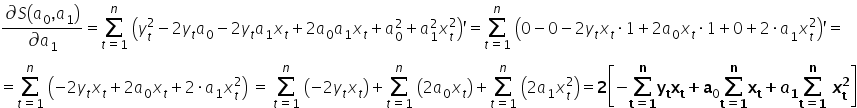
Porównując obliczone pochodne do zera mam dalej:
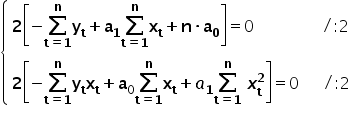
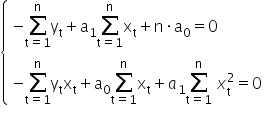
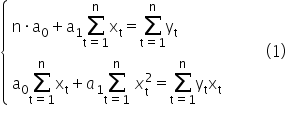
Naszym zadaniem jest rozwiązać powyższy układ równań i wyliczyć z niego wartości 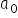 oraz
oraz 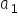 .
.
Zastosuję tu metodę przeciwnych współczynników
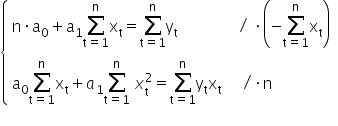
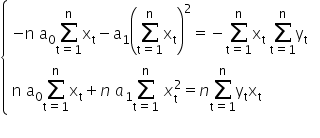
Dodając oba równania do siebie, wychodzi:
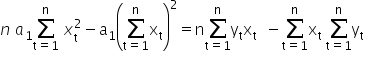
Stąd wyliczymy wartość estymatora 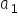 :
:
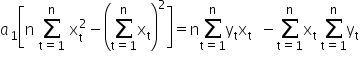
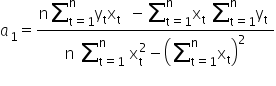
Po małych przekształceniach, ostatecznie wychodzi (dla czytelności nie będę pisała indeksów sumy):
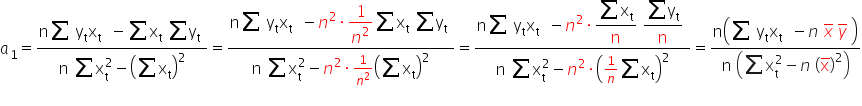
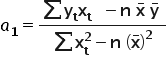
Zostało jeszcze oszacować parametr 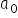 . W tym celu wykorzystam pierwsze równanie z układu równań (1).
. W tym celu wykorzystam pierwsze równanie z układu równań (1).
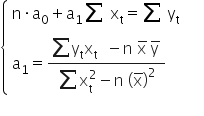
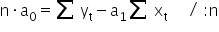
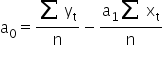
Stąd ostateczne:
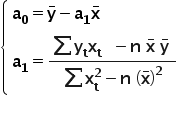
gdzie 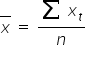 oraz
oraz 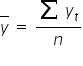 są średnimi arytmetycznymi odpowiednio zmiennych X oraz Y.
są średnimi arytmetycznymi odpowiednio zmiennych X oraz Y.
Po pewnych przekształceniach można również stosować inną wersję wzoru na wartość parametru 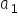 stojącego przy X. Obie są poprawne i obie można śmiało zamiennie wykorzystywać.
stojącego przy X. Obie są poprawne i obie można śmiało zamiennie wykorzystywać.
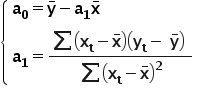
W ten oto sposób wyprowadza się wzory na oszacowania estymatorów parametrów strukturalnych modelu ekonometrycznego. 🙂
Dla osób bardziej wprawionych matematycznie: – skąd wiadomo, że akurat tak wyliczone wartości minimalizują funkcję 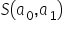 ? W analizie matematycznej , aby to potwierdzić, wyznacza się na początku pochodne cząstkowe drugiego rzędu funkcji po danych parametrach. Pamiętam, że pierwsze pochodne wyglądały następująco:
? W analizie matematycznej , aby to potwierdzić, wyznacza się na początku pochodne cząstkowe drugiego rzędu funkcji po danych parametrach. Pamiętam, że pierwsze pochodne wyglądały następująco: 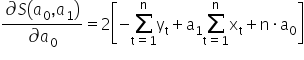 oraz
oraz 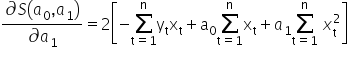 .
.
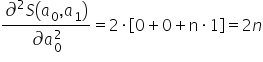
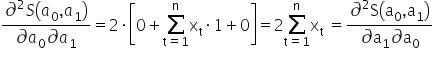
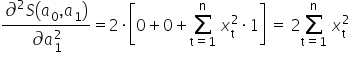
Układam je w tak zwany „Hessjan”, czyli macierz pochodnych drugiego rzędu:
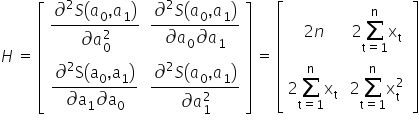
Funkcja dwóch zmiennych posiada ekstremum, gdy zachodzą dwa warunki:
- maksimum lokalne, gdy wartość wyznacznika macierzy w punkcie
 jest dodatnia, tzn.
jest dodatnia, tzn.  oraz
oraz 
- minimum lokalne, gdy wartość wyznacznika macierzy w punkcie
 jest dodatnia, tzn.
jest dodatnia, tzn.  oraz
oraz 
Szukam wartości minimalizującej funkcję 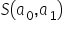 .
.
Drugi warunek minimum lokalnego jest spełniony, gdyż 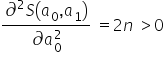 . Sprawdzam więc wyznacznik Hessjanu, czy aby na pewno będzie miał wartość dodatnią. W przypadku macierzy
. Sprawdzam więc wyznacznik Hessjanu, czy aby na pewno będzie miał wartość dodatnią. W przypadku macierzy 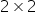 taki wyznacznik łatwo się liczy:
taki wyznacznik łatwo się liczy: 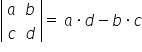 . Stąd:
. Stąd:
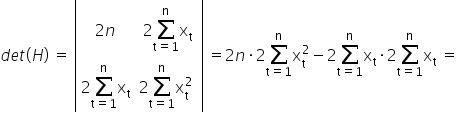
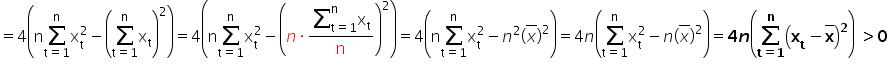
Stąd wyznaczone wartości estymatorów parametrów 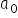 oraz
oraz 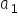 minimalizują funkcję
minimalizują funkcję 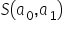 .
.
Interpretacja współczynnika kierunkowego i wyrazu wolnego
Kiedy obliczysz parametry równania regresji liniowej 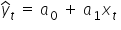 , to warto by było wiedzieć, co one oznaczają.
, to warto by było wiedzieć, co one oznaczają.
Wartość estymatora współczynnika kierunkowego 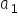 interpretujemy następująco:
interpretujemy następująco:
Wzrost (ZAWSZE wzrost) zmiennej objaśniającej X o 1 jednostkę pociąga za sobą zmianę (wzrost lub spadek) zmiennej objaśnianej średnio/przeciętnie o wartość oszacowanego parametru
.
Wyraz wolny 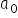 mówi nam, jakiej wartości Y powinniśmy spodziewać się dla zerowego X. Jednak nie zawsze ta interpretacja jest sensowna. Wspominałam o tym w moim Kursie.
mówi nam, jakiej wartości Y powinniśmy spodziewać się dla zerowego X. Jednak nie zawsze ta interpretacja jest sensowna. Wspominałam o tym w moim Kursie.
Przykład 2
W pewnej grupie studentów zbadano zależność liczby punktów, otrzymanych jako wynik egzaminu 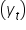 , od godzin nauki do tego egzaminu
, od godzin nauki do tego egzaminu 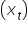 . Po obliczeniach oszacowano model postaci:
. Po obliczeniach oszacowano model postaci: 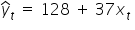 . Interpretacja parametrów modelu jest następująca:
. Interpretacja parametrów modelu jest następująca:
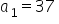 – jeżeli liczba godzin nauki do egzaminu zwiększy się o jedną godzinę, to liczba punktów otrzymanych z egzaminu zwiększy się przeciętnie o około 37 pkt;
– jeżeli liczba godzin nauki do egzaminu zwiększy się o jedną godzinę, to liczba punktów otrzymanych z egzaminu zwiększy się przeciętnie o około 37 pkt;
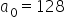 – nie podlega interpretacji. Przecież nie jest sensowne powiedzieć, że jeżeli student nie będzie się uczył do egzaminu (poświęci
– nie podlega interpretacji. Przecież nie jest sensowne powiedzieć, że jeżeli student nie będzie się uczył do egzaminu (poświęci 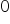 godzin na naukę), to otrzyma z egzaminu aż 128 punktów…
godzin na naukę), to otrzyma z egzaminu aż 128 punktów…
Estymacja parametrów modelu ekonometrycznego Metodą Najmniejszych Kwadratów – przypadek wielu zmiennych objaśniających.
Przed chwilą zostało wyjaśnione jak działa i na czym polega szukanie prostej w przypadku dwóch zmiennych X oraz Y. Model liniowy ze stałą i jedną zmienną objaśniającą jest szczególnym przypadkiem modelu z ilością k zmiennych objaśniających. Zatem jak działa Metoda Najmniejszych Kwadratów w sytuacji, gdy mamy więcej niż jedną zmienną X? W tym przypadku znalezienie rozwiązania staje się względnie proste przy zastosowaniu algebry macierzy.
Ogólny model ekonometryczny z wyrazem wolnym jest postaci:
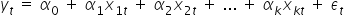
W zapisie macierzowo-wektorowym można przedstawić go następująco:

Stąd:
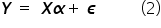
Przy takim zapisie, wektor kolumnowy 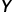 zawiera wszystkie obserwacje dla zmiennej objaśnianej. W macierzy
zawiera wszystkie obserwacje dla zmiennej objaśnianej. W macierzy 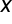 kolejne kolumny stanowią obserwacje zmiennych objaśniających w modelu. Zazwyczaj macierz
kolejne kolumny stanowią obserwacje zmiennych objaśniających w modelu. Zazwyczaj macierz 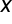 jest macierzą prostokątną o dużo większej liczbie wierszy niż kolumn, ponieważ najczęściej liczba obserwacji jest większa niż liczba zmiennych
jest macierzą prostokątną o dużo większej liczbie wierszy niż kolumn, ponieważ najczęściej liczba obserwacji jest większa niż liczba zmiennych 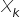 . Macierzy
. Macierzy 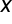 jako macierzy prostokątnej nie da się odwrócić (tylko macierze kwadratowe są odwracalne). Z tego też względu równania (2) nie da się rozwiązać za pomocą czysto algebraicznych przekształceń.
jako macierzy prostokątnej nie da się odwrócić (tylko macierze kwadratowe są odwracalne). Z tego też względu równania (2) nie da się rozwiązać za pomocą czysto algebraicznych przekształceń.
Model ekonometryczny po oszacowaniu parametrów strukturalnych 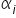 będzie w postaci:
będzie w postaci:
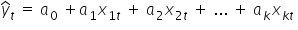
Pokażę teraz, jak wyprowadza się estymator 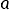 parametrów Metodą Najmniejszych Kwadratów.
parametrów Metodą Najmniejszych Kwadratów.
Zasada jest taka sama jak poprzednio. Idea MNK sprowadza się do takiego wyznaczenia wartości ocen 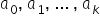 parametrów strukturalnych
parametrów strukturalnych 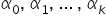 , aby suma kwadratów różnic wartości obserwowanych
, aby suma kwadratów różnic wartości obserwowanych 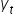 i wartości teoretycznych obliczonych z równania modelu
i wartości teoretycznych obliczonych z równania modelu 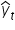 były jak najmniejsze.
były jak najmniejsze.
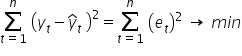
Podobnie jak poprzednio, po podstawieniu równania teoretycznego modelu, otrzymuję:
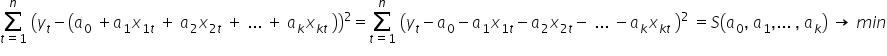
Rozwiązaniem układu w postaci macierzowej będzie wektor postaci: 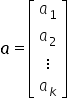 .
.
Funkcję 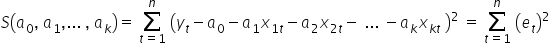 , wykorzystując własności działań na macierzach, w postaci macierzowej można rozpisać następująco:
, wykorzystując własności działań na macierzach, w postaci macierzowej można rozpisać następująco:
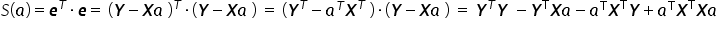
Suma kwadratów reszt 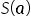 jest jedną konkretną liczbą, inaczej skalarem. Tak więc każdy element uzyskanej sumy również jest zwykłą liczbą. Transpozycja skalarów czy też zamiana kolejności mnożenie nie wpływa na wynik, więc:
jest jedną konkretną liczbą, inaczej skalarem. Tak więc każdy element uzyskanej sumy również jest zwykłą liczbą. Transpozycja skalarów czy też zamiana kolejności mnożenie nie wpływa na wynik, więc: 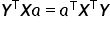 . W rezultacie wychodzi:
. W rezultacie wychodzi:
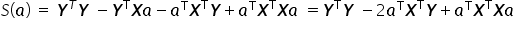
Funkcja 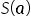 osiąga minimum, jeśli jej pierwsza pochodna względem wektora
osiąga minimum, jeśli jej pierwsza pochodna względem wektora 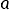 jest równa wektorowi zerowemu, a druga pochodna jest dodatnio określona.
jest równa wektorowi zerowemu, a druga pochodna jest dodatnio określona.
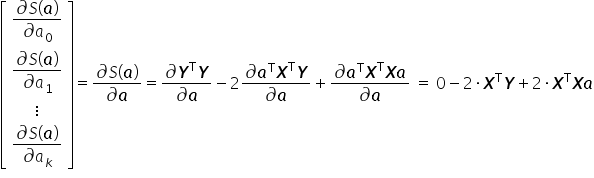
Przyrównując pochodną 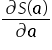 do wektora zerowego otrzymuję:
do wektora zerowego otrzymuję:
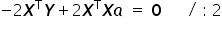
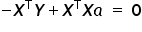
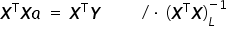
Z własności mnożenia macierzy 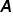 i macierzy do niej odwrotnej
i macierzy do niej odwrotnej 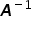 otrzymujemy macierz jednostkową, czyli:
otrzymujemy macierz jednostkową, czyli: 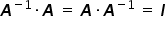 . Jest to macierz odpowiadająca po prostu liczbie jeden.
. Jest to macierz odpowiadająca po prostu liczbie jeden.
Stąd ostatecznie otrzymujemy wzór na oszacowania nieznanych parametrów strukturalnych 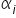 w postaci wektorowej:
w postaci wektorowej:
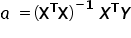
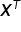 oznacza macierz transponowaną do macierzy
oznacza macierz transponowaną do macierzy 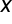 , natomiast
, natomiast 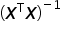 oznacza macierz odwrotną do macierzy
oznacza macierz odwrotną do macierzy 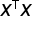 .
.
Jak dotąd rozpatrywany był warunek konieczny istnienia ekstremum. Należy teraz zbadać, czy rzeczywiście znalezione ekstremum jest minimum funkcji 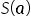 . Warunek dostateczny istnienia ekstremum sprowadza się do tego, aby Hessjan, czyli macierzy drugich pochodnych była dodatnio określona. W tym przypadku będzie miała ona postać:
. Warunek dostateczny istnienia ekstremum sprowadza się do tego, aby Hessjan, czyli macierzy drugich pochodnych była dodatnio określona. W tym przypadku będzie miała ona postać:
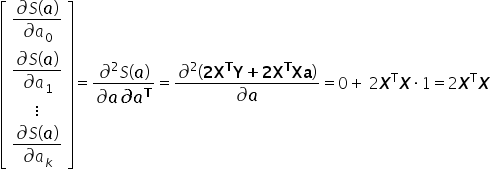
Powyższe równanie jasno wskazuje na fakt, że warunek dodatniej określoności Hessjanu jest spełniony, ponieważ 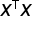 jest dodatnio określona, jeśli tylko jej wyznacznik jest różny od zera.
jest dodatnio określona, jeśli tylko jej wyznacznik jest różny od zera.
Interpretacja współczynników 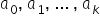
Podobnie jak w przypadku równania z jedną zmienną objaśniającą, warto też wiedzieć jak interpretować parametry równania regresji liniowej 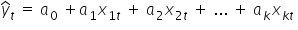 .
.
W tym przypadku, nasz tok myślenia powinien pójść bardzo analogicznie co do wcześniej omawianego przypadku jednej zmiennej objaśniającej. Różnica będzie dotyczyła dodania do poprzedniej interpretacji frazy o stałości pozostałych zmiennych (nie interpretowanych w danym momencie). A co za tym idzie, wartość estymatora współczynnika 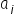 , stojącego przy zmiennej
, stojącego przy zmiennej 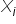 , gdzie
, gdzie 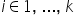 , interpretujemy następująco:
, interpretujemy następująco:
Wzrost (ZAWSZE wzrost) zmiennej objaśniającej
o 1 jednostkę pociąga za sobą zmianę (wzrost lub spadek) zmiennej objaśnianej
średnio/przeciętnie o wartość oszacowanego parametru
, przy założeniu stałości pozostałych zmiennych (ceteris paribus).
Tak jak poprzednio, wyraz wolny 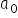 mówi nam, jakiej wartości Y powinniśmy się spodziewać dla zerowych wartości wszystkich zmiennych objaśniających. Jednak w przypadku zmiennych ekonomicznych, nie zawsze ta interpretacja jest sensowna, co pokazuje Przykład 2.
mówi nam, jakiej wartości Y powinniśmy się spodziewać dla zerowych wartości wszystkich zmiennych objaśniających. Jednak w przypadku zmiennych ekonomicznych, nie zawsze ta interpretacja jest sensowna, co pokazuje Przykład 2.
Stąd oto biorą się i w ten sposób zostały wyprowadzone wzory na oszacowania parametrów modelu ekonometrycznego Metodą Najmniejszych Kwadratów.
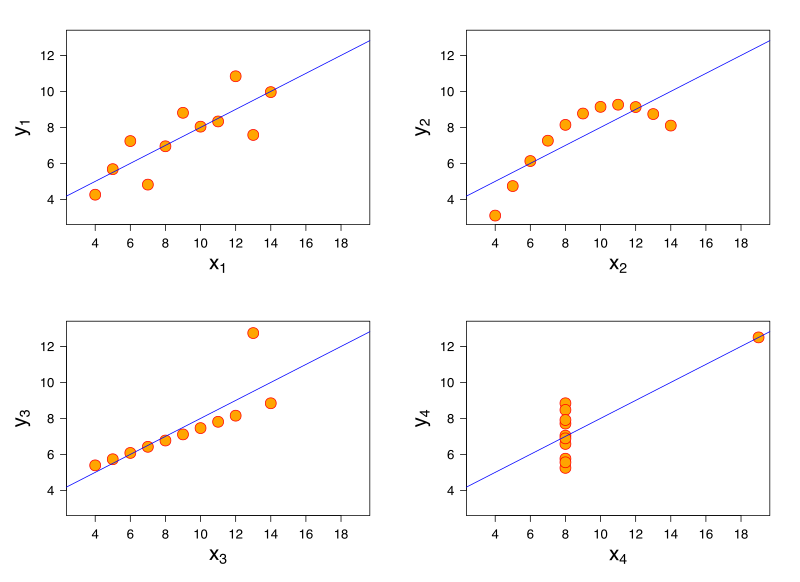
Ciekawostka – Kwartet Anscombe’a
Wszystko co ma plusy, ma i swoje minusy. Niedostateczność Metody Najmniejszych Kwadratów w ogólnym przypadku pokazuje m.in. kwartet Anscombe’a – specjalnie przygotowany zestaw czterech zbiorów danych, które mają niemal tożsame wskaźniki statystyczne (średnią i wariację w kierunku X i Y, współczynnik korelacji oraz prostą regresji) pomimo znacząco różnego charakteru danych w ujęciu graficznym.
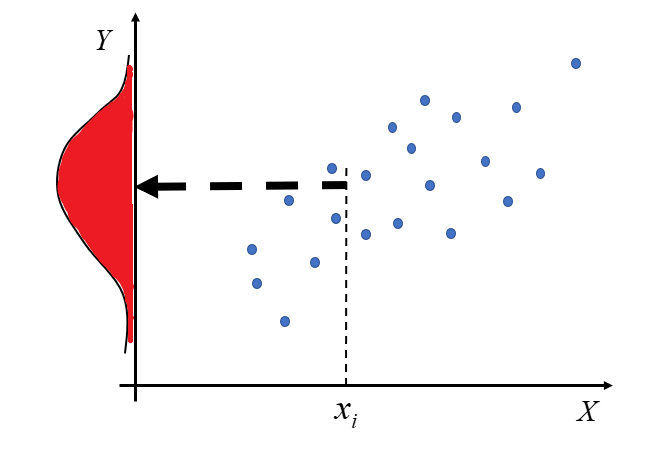
Na koniec niniejszego artykułu wspomnę jeszcze o jednej ważnej własności. Korzystając z Metody Najmniejszych Kwadratów otrzymane estymatory 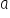 oszacowań parametrów modelu mają następujące własności: są liniowe, zgodne, nieobciążone i najefektywniejsze. Ale o tym wszystkim w następnych wykładach.
oszacowań parametrów modelu mają następujące własności: są liniowe, zgodne, nieobciążone i najefektywniejsze. Ale o tym wszystkim w następnych wykładach.
Podsumowanie
W powyższym Wykładzie zaprezentowałam pojęcie „regresji” oraz działanie najszerzej stosowanej w ekonometrii metody estymacji, zwanej Metodą Najmniejszych Kwadratów. To właśnie za jej pomocą szacując nieznane parametry modelu, uzyskujemy oszacowania, dla których model najlepiej opisuje zaprezentowane dane.
Mam nadzieję, że odtąd stosowane wzory nie będą już dla Ciebie żadną tajemnicą.
Jeśli chcesz zastosować poznaną wiedzę w praktyce, zachęcam Cię do zajrzenia do mojego Kursu, zwłaszcza do lekcji nr 3.
KONIEC
Kliknij, aby powrócić na stronę z Wykładami do ekonometrii

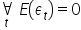 ;
;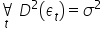 ;
;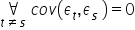 .
.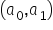 jest dodatnia, tzn.
jest dodatnia, tzn. 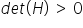 oraz
oraz 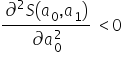
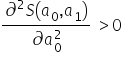
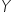 średnio/przeciętnie o wartość oszacowanego parametru
średnio/przeciętnie o wartość oszacowanego parametru 