Metoda grafów – jak inaczej wybrać zmienne objaśniające do modelu

---

Tworząc model ekonometryczny kluczowym etapem jest wybór zmiennych objaśniających. W moim Kursie Ekonometria szczegółowo i dokładnie pokazałam najbardziej powszechną i najczęściej używaną metodę Hellwiga. Poznać ją możesz w Lekcji nr 2. 

Jednak poza nią istnieje szereg innych równie ciekawych metod doboru zmiennych objaśniających. Jedną z nich, metodę analizy współczynników korelacji (metodę Bartosiewicz), już wcześniej zaprezentowałam na Blogu. Zachęcam, byś zajrzał do poniższego artykułu i filmiku:

Jak wybrać zmienne do modelu, czyli metoda analizy współczynników korelacji (VIDEO)

 

Natomiast w tym artykule chciałabym przedstawić Ci kolejną metodę jaką jest METODA GRAFÓW, czasami nazywana metodą grafową.

Idea tej metody, podobnie jak w metodzie pojemności informacyjnej Hellwiga, opiera się na wyborze takich zmiennych objaśniających do modelu, które są silnie skorelowane ze zmienną objaśnianą 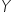, a jednocześnie słabo powiązane między sobą. 

Procedura metody rozpoczyna się od utworzenia dwóch podstawowych macierzy. Pierwsza to macierz, a raczej wektor korelacji 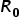pomiędzy zmienną objaśnianą 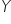, a wszystkimi kandydatkami na zmienne objaśniające .

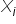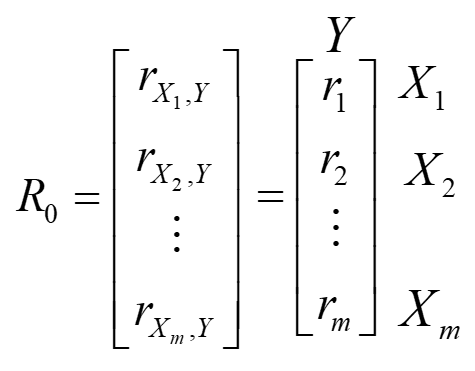
Druga macierz 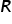, to macierz korelacji między samymi już zmiennymi objaśniającymi 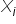a .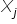

 

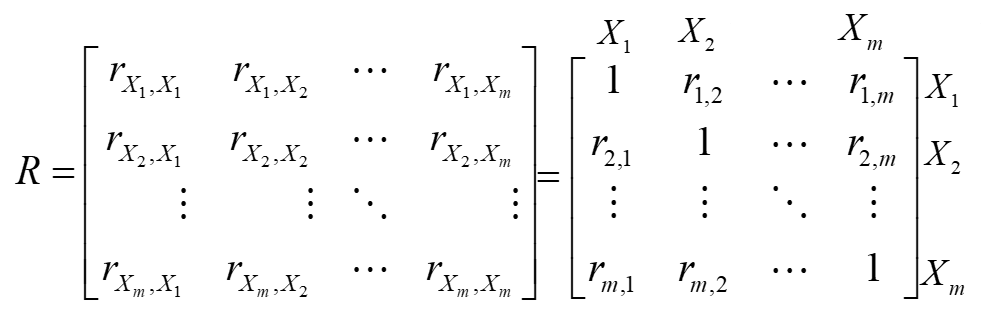
Kolejnym etapem jest sprawdzenie, które elementy macierzy 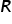są tak małe, że można by je uznać za zerowe (nieistotnie rożne od zera). W tym celu musimy porównać wszystkie rzeczywiste współczynniki korelacji  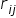z macierzy 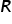ze współczynnikiem krytycznym. Można go wyznaczyć ze wzoru:

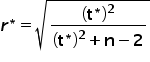gdzie 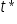oznacza wartość krytyczną statystyki odczytanej z tablic t-Studenta dla danego poziomu istotności 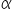oraz 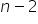stopni swobody. Wartość 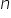oznacza oczywiście liczbę obserwacji w modelu. 

Także jak widzisz, początkowe dane i wartość krytyczna wyznacza się identycznie jak np. w opisanej wcześniej metodzie Bartosiewicz. Jednak sama procedura będzie przebiegała już lekko inaczej. Na konkretnym przykładzie zaprezentuję Ci kolejne kroki:

 

Przykład

Chcemy wybrać do modelu ekonometrycznego zestaw najlepszych zmiennych objaśniających spośród pięciu zaprezentowanych: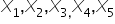. W tym celu dla każdej zmiennej zebrano 28 kolejnych obserwacji. Mamy następujące macierze 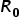i  :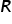

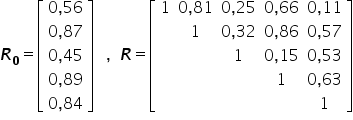
Dla poziomu istotności 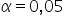 oraz przy liczbie obserwacji  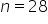odczytujemy z tablic rozkładu t-Studenta 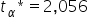, a zatem: 

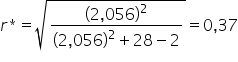
Krok 1.

Porównujemy współczynniki korelacji 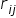z macierzy 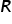ze współczynnikiem krytycznym 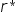. Wszystkie mniejsze elementy zastępujemy zerem, tzn takie, gdzie 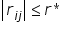. Powstaje w sten sposób macierz .

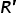W naszym przykładzie wszystkie wartości co do moduły mniejsze od 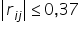zastępuje zerem. Od razu “skopuję” pozostałą część tablicy, gdyż wiemy, że jest ona symetryczna względem głównej przekątnej. Stąd:

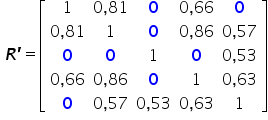
Krok 2.

Na podstawie powstałej macierzy 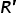budujemy GRAF POWIĄZAŃ między zmiennymi. Wierzchołki to potencjalne zmienne objaśniające, a wiązadła (czyli linie łączące dane wierzchołki) to niezerowe elementy macierzy .

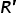W naszym przykładzie będzie ten graf wyglądał następująco: 

 

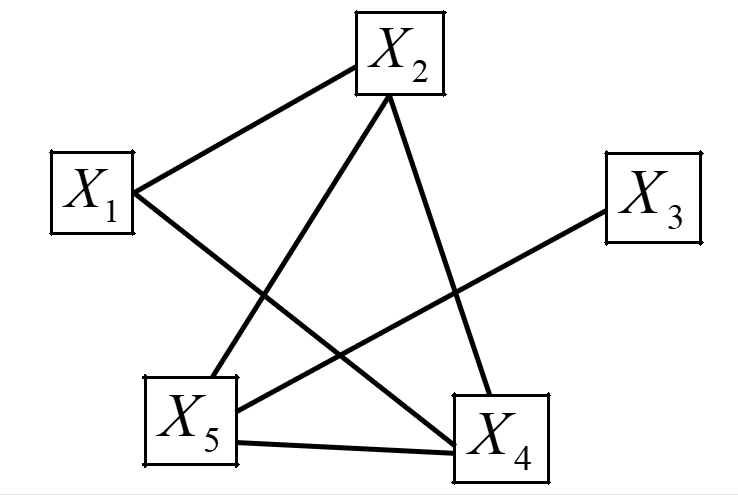
Krok 3.

Możemy otrzymać graf spójny (wszystkie punkty są ze sobą połączone w pewną sieć) lub kilka grafów, a także punkty (zmienne) odosobnione. Z tak powstałych podgrafów do modelu wybieramy zmienne odosobnione (nie są one bowiem skorelowane z innymi potencjalnymi zmiennymi objaśniającymi). Także wybieramy te zmienne, które mają największą liczbę powiązań (wiązadeł) z innymi potencjalnymi zmiennymi objaśniającymi. Z tej grupy wybieramy jedną zmienną, która jest najsilniej skorelowana ze zmienną objaśniającą.

Taki wybór podyktowany jest tym, że zmienna o największej ilości wiązadeł w grafie gromadzi w sobie najwięcej informacji o pozostałych zmiennych (z którymi była powiązana). A zatem będzie dobrą ich reprezentantką. 

Patrząc na nasz przykład. NIE mamy żadnych punktów odizolowanych (punktów do których nie dochodziłaby żadna kreseczka). Zatem wybieramy zmienne, które mają największa ilość powiązań. Będą to zmienne, do których dochodzą aż trzy kreski, czyli: 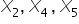. Musimy wybrać spośród nich jedną zmienną – tą, która jest najsilniej skorelowana ze zmienną objaśniającą 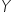. Zatem patrzę teraz na macierz :

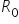Jak widać najbardziej powiązana jest zmienna 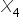. Zatem tylko ta jedna zmienna zostanie w tym przypadku zmienną objaśniającą. 

Model nasz będzie postaci: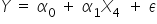

 

Jak widać ta metoda jest troszkę inna, bazująca na wydaje się prostym porównaniu współczynników i potem wzrokowej analizie grafu. Zatem powinna spodobać się osobom, które wolą coś więcej niż tylko same cyferki. 🙂