Ekonometria Wykład 1
Temat: Co to jest ekonometria?
Wiele osób mnie pytało:
ekonometria – cóż to takiego jest?
Zwłaszcza słysząc, że studiuję „informatykę i ekonometrię” (tak, tak, o dziwo istnieje taki kierunek studiów). Nazwa jest intrygująca, to prawda. Jednak jak się okazuje sama istota tej całej ekonometrii jest ciekawa. Można by nawet powiedzieć, że „życiowa”, czyli w końcu coś, czego się uczymy, można wykorzystać w prawdziwym życiu 🙂
Co potrzeba by zacząć przygodę z ekonometrią?
Kalkulator do prostych obliczeń, podstawowe informacje na temat różnych funkcji, trochę wyobraźni i umiejętność kojarzenia faktów. Reszta przyjdzie sama.
Na początek krótki przykład.
Przykład 1
W pewnej grupie losowo wybranych studentów zapytano ich, ile czasu poświęcili na naukę przed ważnym kolokwium (w godzinach). Później sprawdzono, jaką dostali ocenę. W tabelce zapisano wyniki:
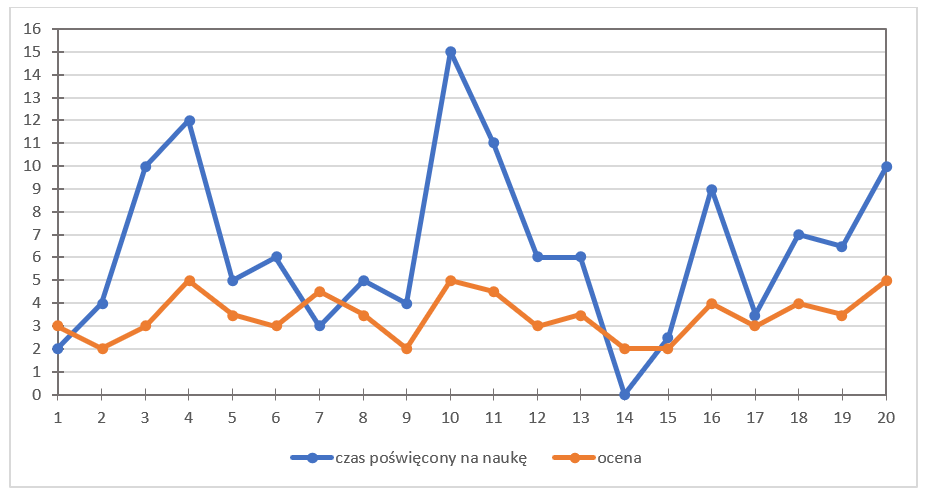
Hmm…, takie popatrzenie na gołe cyferki nie każdemu powie cokolwiek. Dlatego warto dla każdej z cech wykonać na początku odrębny wykres, tzn. dla danego studenta zaznaczyć wartość oceny oraz czasu jego nauki.
Oto on:
Skąd akurat takie „falki”? Oś OX oznacza kolejny numer studenta, zaś oś OY odzwierciedla wartość oceny (ten pomarańczowy wykresik), oraz ilość czasu poświęconego na naukę (niebieski wykres). Odpowiednie odznaczanie par punktów jest bardzo ważne, dlatego na spokojnie przypatrz się tabelce i zaznaczonym kropeczkom.
Specjalnie umieściłam oba te wykresy na jednym schemacie. Dlaczego? By popatrzeć i móc przeanalizować wizualnie jak zachowują się te zmienne nie względem kolejnego studenta, ale ogólnie WZGLĘDEM SIEBIE. Może jest jakaś zależność, powiązanie między czasem nauki, a oceną z kolokwium?
Na pewno widzisz, że te wykresy mają co raz to „górki” i „doły”. Czy te szczyty i dołki jakoś się pokrywają? To znaczy, czy występują u danego studenta jednocześnie?
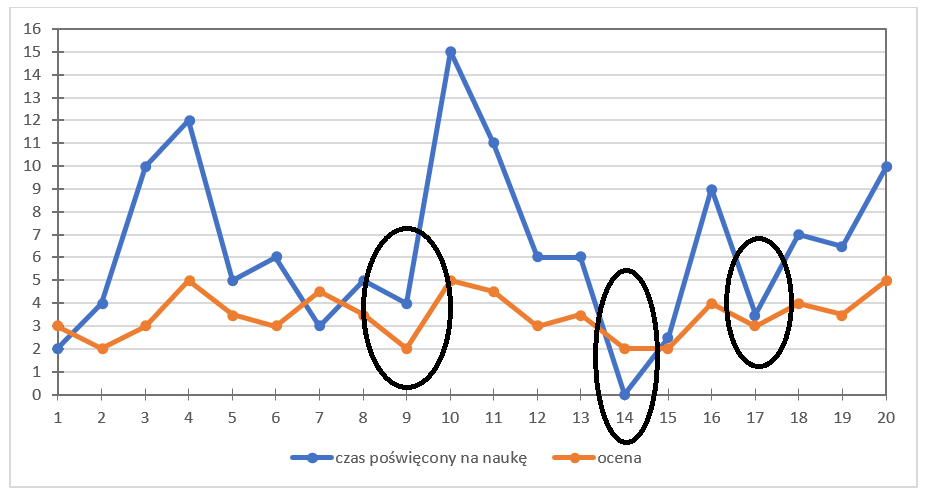
Oczywiście, masz rację, widać tu wyraźnie takie coś, bo np. są takie górki:
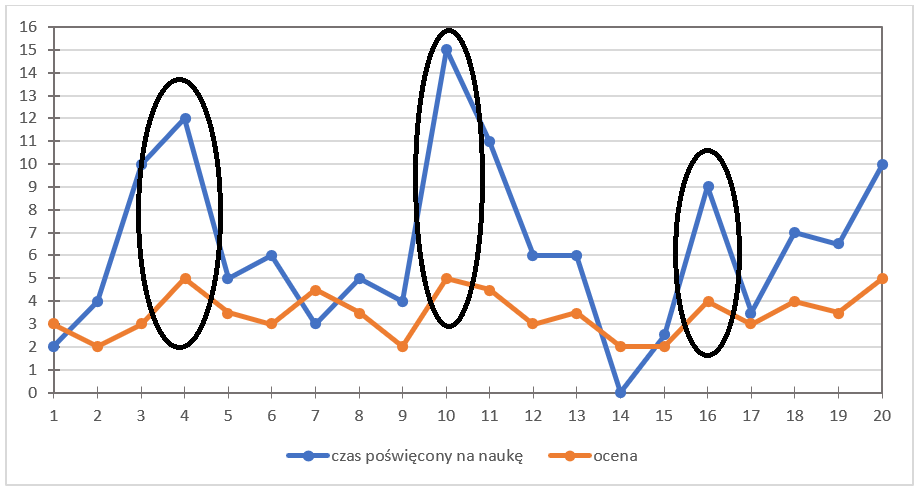
a tu doły:
Jak widzisz, analizując dane odzwierciedlające jakieś konkretne zjawisko (fakt, nauka przed kolokwium u niektórych osób może być „zjawiskiem”, fenomenem 🙂 ), możesz tu zauważyć pewne ZALEŻNOŚCI. Co powiesz na ich temat?
Dokładnie, widać tu (zwłaszcza na podstawie wykresu), że im dłużej się uczysz, tym lepsza i wyższa jest ocena (i na odwrót). Z reguły to jest prawdziwe. Nawet bardzo prawdziwe. Bynajmniej trzeba mieć na uwadze, że od każdej reguły są wyjątki. (Tu mi się przypomniało takie powiedzenie: Umiesz na 2, liczysz na 3, dostajesz 4, zastanawiasz się czemu nie 5. 🙂 ).
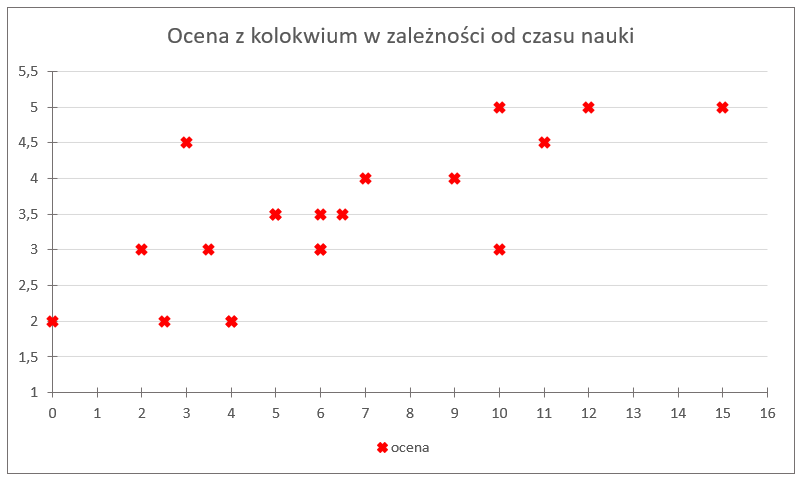
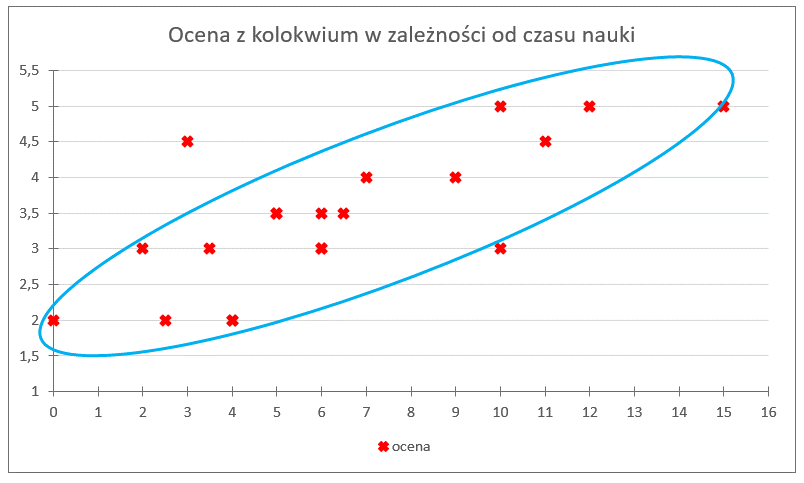
Dobrze, skoro doszliśmy do wniosku, że istnieje jakaś zależność miedzy tymi dwiema cechami, spróbujmy dla tych danych zrobić kolejny wykres – tym razem uzależniając czas nauki od oceny. To znaczy, że parami punktów które zaznaczymy w układzie współrzędnych nie będzie numer studenta i dana cecha, ale uwzględnijmy tylko dwie cechy, tzn:
Powiedzmy, że czas nauki to będzie nasza zmienna X, natomiast otrzymana ocena to zmienna Y. Stąd mamy zaznaczone punkty:
Tutaj jak widać trochę ciężko będzie z połączeniem wszystkich kropek w jedną łamaną linię. No się nie da. Jednak ta „chmura” punktów układa się pewien charakterystyczny sposób, zobacz:
Co powiesz o tym kształcie? Nachyleniu?
Jak widać, układa się on tak „ładnie”, podłużnie, chyląc się ku górze. Czyli nasza zauważona zależność (wzrost czasu nauki pociąga za sobą wyższą ocenę) jest potwierdzona. Co do kształtu, można by pójść krok do przodu i powiedzieć nawet, że ma on charakter liniowy, że bliski jest jednej rosnącej linii prostej, która by „ogarniała” całą tą chmurę punktów.
Wyszło, że istniejącą prawidłowość między dwiema cechami da się ująć jakoś matematycznie. A jednak!
Oczywiście trzeba mieć cały czas z tyłu głowy, że NIE jest to dokładna charakterystyka tego powiązania, tylko jej przybliżona funkcja próbująca jak najlepiej opisać daną zależność. Tutaj akurat mamy coś podobnego do linii prostej, czyli funkcji liniowej.
Skoro ustaliliśmy, że tę większą większość punktów da się ogarnąć jedną funkcją, można więc powiedzieć, że da się je ZMIERZYĆ. Zostaje więc tylko wskazać jak tą funkcję stworzyć, wyliczyć i w ogóle do czego nam się to przyda?
Z pomocą przychodzi właśnie ekonometria!
Pojęcie ekonometrii
Całkiem niedawno, na początku XX wieku, znalazł się pewien Polak, który z dwóch słówek greckich iokonomia (ozn. administracja, gospodarka) oraz metron (ozn. miara) i utworzył nowy wyraz – ekonometria. W dosłownym znaczeniu jest to MIERZENIE GOSPODARKI.
W sumie brzmi logicznie 🙂 Ponieważ właśnie na tym (w ogólnym sensie) polega cała ekonometria – na zmierzeniu prawidłowości zachodzących w zjawiskach ekonomicznych, za pomocą pewnych metod matematycznych oraz statystycznych. Wyjaśnia ona po prostu zachowanie jednej zmiennej, w zależności od zachowania innych zmiennych.
Czyli nie tylko matematyka gra tu istotną rolę, ale również i statystyka. Dane nie powinny być ot tak wzięte z głowy, ale najlepiej aby były one rzeczywiste. Na dane, które zebrano i spisano, mówi się, że są to dane statystyczne. Dlatego też ekonometrię można nazwać takim naturalnym „dzieckiem” statystyki.
Wracając do przykładu. Zauważyliśmy pewną zależność wśród zmiennych konkretnych, „życiowych”, można więc śmiało powiedzieć, że wśród zmiennych ekonomicznych.
Przypuśćmy teraz, że kolejny student, nr 21, na podstawie analizy danych doświadczeń kolegów chciałby tak mniej więcej „wyliczyć” ile czasu ma się pouczyć, by otrzymać pożądaną ocenę (załóżmy, że jemu spokojnie 3 lub 3,5 wystarczy). Lub też – jeśli będzie się uczył pół dnia, jakiej oceny może się spodziewać?
By odpowiedzieć na te pytania, czyli by móc coś „wyliczyć”, potrzebne nam jest konkretne równanie. Tu pojawia się kolejne pojęcie – model ekonometryczny.
Pojęcie modelu ekonometrycznego
Podstawowym narzędziem wykorzystywanym w analizie ekonometrycznej jest model ekonometryczny. Model (nie, to nie męska wersja modelki 🙂 ) to formalna konstrukcja teoretyczna, która podlega analizie w miejsce rzeczywistego zjawiska. Pozwala na lepsze zrozumienie jego charakteru. Za pomocą jednego lub kilku równań przedstawia powiązania występujące pomiędzy elementami wybranych przez nas cech ekonomicznych. Zatem jest to model matematyczny, który został „dopasowany” do rzeczywistości za pomocą odpowiednich metod statystycznych.
Miej to na uwadze, że jest on zawsze znacznie uproszczonym obrazem obserwowanego zjawiska. Tak jak np. model samolotu czy model spirali DNA. Pokazuje „obrazowo” coś, co istnieje w świecie realnym. Nadmienię od razu, że model ekonometryczny uwzględnia najistotniejsze elementy opisu rzeczywistości. Pomija zaś te mniej ważne. Tutaj chyba się ze mną zgodzisz, bo przecież nie jesteśmy w stanie wziąć pod uwagę wszystkich, a to wszystkich możliwości 🙂
Formalnym zapisem modelu jest równanie. Tak wygląda jego najbardziej ogólna postać:
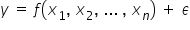 Z czego się składa taki model? Ma kilka stałych elementów:
Z czego się składa taki model? Ma kilka stałych elementów:
Po pierwsze, zmienna 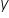 – zmienna, której zachowanie chcesz wyjaśnić za pomocą modelu. Dlatego nazywana jest „zmienną objaśnianą”.
– zmienna, której zachowanie chcesz wyjaśnić za pomocą modelu. Dlatego nazywana jest „zmienną objaśnianą”.
Zmienne 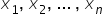 to kolejne n „zmiennych objaśniających”. One posłużą do wyjaśniania. Czasami wystarczy, by była tylko jedna zmienna objaśniająca. Mają one oczywiście ustaloną treść ekonomiczną.
to kolejne n „zmiennych objaśniających”. One posłużą do wyjaśniania. Czasami wystarczy, by była tylko jedna zmienna objaśniająca. Mają one oczywiście ustaloną treść ekonomiczną.
Funkcja 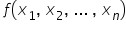 jest zapisem typu związku funkcyjnego między zmienną objaśnianą, a zmiennych objaśniającymi, oraz składnikiem losowym.
jest zapisem typu związku funkcyjnego między zmienną objaśnianą, a zmiennych objaśniającymi, oraz składnikiem losowym.
Właśnie, ta tajemnicza literka 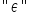 , takie jakby ładnie napisane „E” to epsilon to litera grecka. Ona z kolei oznacza tzw. „składnik losowy”. Dwa zdania o nim.
, takie jakby ładnie napisane „E” to epsilon to litera grecka. Ona z kolei oznacza tzw. „składnik losowy”. Dwa zdania o nim.
Składnik losowy obrazuje w danym modelu „zakłócenia” innymi czynnikami. Równanie matematyczne zawsze traktujemy jako przybliżoną wartość. Dlatego też składnik losowy uwzględnia m.in.: różnice między modelem a rzeczywistością; wpływ innych zmiennych niż te, które są już w modelu; błędy pomiaru zmiennych, czy też działanie czynników losowych, niespodziewanych.
Ufff, ile teorii.
Wracając do naszego przykładu. Ustaliliśmy, że te dwie cechy łączy zależność liniowa. I tu przyda się nam wiedza z gimnazjum – jak wyglądał wzór na funkcję liniową?
Ano szło tak: 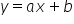 .
.
Zmienne są po prostu do siebie dodawane, przemnożone przez odpowiednie skalary, czyli tzw. „parametry” (a, b). Zatem czy to będzie nasz model?
Odpowiedź brzmi – PRAWIE TAK 🙂
Zapisane równanie stanowi model TEORETYCZNY. By odróżnić go w zapisie od takiego ogólnego modelu, dodaje się nad y daszek. Równanie
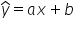
można już uznać za teoretyczny model ekonometryczny.
Nie tak trudno nam poszło 🙂
Jak wyglądałby w postaci ogólnej? Czyli uwzględniającej wszystko, wraz z tymi zmiennymi pominiętymi i mało istotnymi? Tak o:
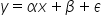
Jest to przypadek dla tej jednej zmiennej. A dla więcej zmiennych:
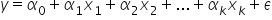
Najczęściej w zapisach formalnych tak już jest, że wykorzystuje się kojne greckie litery (alfa, beta, itd…) do opisu parametrów, czyli tego, co wyrazimy później liczbami.
W naszym przykładzie wyjaśnialiśmy zależność oceny z kolokwium od czasu nauki do niego. A może związek powinien być odwrotny, tzn. czas nauki zależy od oceny? Możemy zatem rozpatrywać model taki:
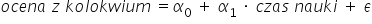
lub taki:
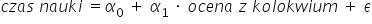
Tutaj przydaje się nam nasza racjonalna wiedza oraz pewna znajomość relacji przyczynowo-skutkowych. Ponieważ jak widać ten drugi model jest pozbawiony sensu. Bo kto by mierzył czas nauki do kolokwium mając już z niego ocenę? 🙂
Zatem model ogólny jest postaci: 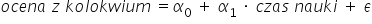 .
.
Co kryje się pod tym „epsilonem”?
Inne zmienne, których nie uwzględniamy, np. ilość obecności na wykładzie, samopoczucie wykładowcy, itp. Są też ukryte zdanie losowe, np. nagła choroba studenta – mimo, iż się uczył bardzo dużo, przez osłabienie i zmniejszoną koncentrację dostał słabszą ocenę.
W tej chwili zadaniem ekonometrii jest odpowiednie wyliczenie wartości 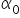 oraz
oraz 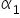 . Otrzymamy wtedy wartości liczbowe, oszacowane, oznaczane jako
. Otrzymamy wtedy wartości liczbowe, oszacowane, oznaczane jako 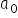 oraz
oraz 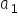 lub jak ktoś woli odpowiednio
lub jak ktoś woli odpowiednio 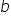 oraz
oraz 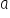 . Na przykład coś takiego:
. Na przykład coś takiego:
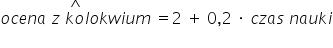
Jak się wylicza te wartości liczbowe, to już jest inny temat 🙂
Metod jest wiele. Każda ma swoje przesłanki do zastosowania. W tym konkretnym modelu uznaliśmy zależność liniową. Jest ona najprostsza w weryfikacji oraz zastosowaniu.
Oczywiście funkcja 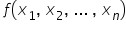 , która opisuje powiązania między zmiennymi objaśniającymi może być dowolna (i wykładnicza, i logarytmiczna, i wymierna, itp. i mieszanka kilku na raz). Teraz zostaje nam tylko sprawdzenie czy model jest dobry (czy spełnia odpowiednie założenia), oraz wyciągniecie pewnych wniosków i zastosowanie go, na przykład do wyliczenia pożądanych wartości dla studenta nr 21.
, która opisuje powiązania między zmiennymi objaśniającymi może być dowolna (i wykładnicza, i logarytmiczna, i wymierna, itp. i mieszanka kilku na raz). Teraz zostaje nam tylko sprawdzenie czy model jest dobry (czy spełnia odpowiednie założenia), oraz wyciągniecie pewnych wniosków i zastosowanie go, na przykład do wyliczenia pożądanych wartości dla studenta nr 21.
Jak widzisz, ekonometria nie jest wcale takim nudnym przedmiotem. Oczywiście liczenia trochę jest – sporo różnych cyferek, wzorów, schematów (jak zawsze w statystyce). Jednak jeśli dobrze się zastanowisz nad tym co chcesz wyjaśnić, wybierzesz odpowiednie zmienne, od których by to zjawisko zależało (nie koniecznie jedna, śmiało, więcej wymyśl 🙂 ), to będziesz mógł pobawić się w wyznaczanie zależności (siły, kierunku), czy też praktyczne wyznaczanie „nowych” wartości.
Efekty mogą Ciebie zadziwić 🙂
KONIEC
Kliknij, aby dowiedzieć się, czym jest model ekonometryczny (następny Wykład) –>
Kliknij, aby powrócić na stronę z Wykładami do ekonometrii





2 Komentarzy
Loszka z ZSH
Pozdrawiam z lekcji ppwza elo
Kis
Każdy wykres powinien mieć opisane osie.