Abiturienten fragen, eTrapez antwortet. Herleitung der Höhenformel im rechtwinkligen Dreieck.
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Dieser Beitrag ist einem Teil einer Abituraufgabe gewidmet, den mir ein Abiturient per E-Mail geschickt hat. Es lohnt sich jedoch aus Neugier einen Blick darauf zu werfen und nie wieder zu sagen, dass Mathematik an der Universität schwieriger ist als im erweiterten Schulunterricht.
🙂
Ein Stück der Aufgabe
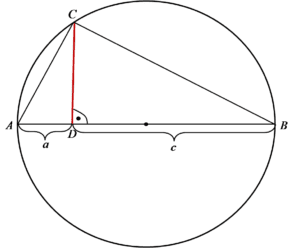
Wir haben folgende Situation:
Es soll gezeigt werden, dass das rot markierte Segment eine Länge von 
hat. Dies ist natürlich nur ein winziger Teil der gesamten Aufgabe. Ratet mal, worum es geht? Um Folgen natürlich 🙂
Also, wir können hier einen häufig verwendeten Trick in Aufgaben zur Höhe eines rechtwinkligen Dreiecks anwenden, nämlich die “beliebten” ähnlichen Dreiecke aller Abiturienten.
1. Die Dreiecke 
(das kleinste) und 
(das größte, im Kreis eingeschrieben) sind ähnlich (sie haben 2 gleiche Winkel: recht und <DAC, also ist der dritte Winkel auch gleich, das heißt, wir haben eine AA-Ähnlichkeit). Die Dreiecke 
(das mittlere) und (das größte wieder) sind ebenfalls ähnlich (sie haben 2 gleiche Winkel: recht und <CBD, also ist der dritte Winkel auch gleich, wir haben also wieder eine AA-Ähnlichkeit). Wenn die Dreiecke und ähnlich zu sind, dann sind sie auch ähnlich zueinander, und das ist es, was wir bemerken:
ist ähnlich zu
2. Wenn diese Dreiecke ähnlich sind, dann sind die Verhältnisse der entsprechenden Seiten gleich. Natürlich wählen wir die Verhältnisse, die das rot markierte Segment enthalten, dessen Länge wir als 
bezeichnen.
Im Dreieck ist das Verhältnis der KÜRZESTEN Seite zur MITTLEREN Seite gleich:
Im Dreieck ist das Verhältnis der KÜRZESTEN Seite zur MITTLEREN Seite gleich:
Da die Dreiecke ähnlich sind, besteht eine Gleichung:
3. Aus dieser Gleichung bestimmen wir h, also die Länge des rot markierten Segments. Wir multiplizieren über Kreuz wie in Verhältnissen üblich und erhalten:
Das bedeutet:
Das bedeutet genau das, was wir am Anfang zeigen sollten. BINGO.
Die Moral der Geschichte: Beim Bestimmen der Höhe in einem rechtwinkligen Dreieck (diejenige, die auf die Hypotenuse fällt natürlich) müssen wir oft die Ähnlichkeit von Dreiecken verwenden, wie oben gezeigt.
Und noch eine Moral: Erweiterte Mathematik in der Schule konnte wirklich herausfordernd sein. Erst an der Universität können wir aufatmen 🙂
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
