Es befinden sich momentan keine Produkte im Warenkorb.
Krystian Karczyński- 6 August 2024
- Komentarz 0
Es gibt Tage, an denen einfach nichts funktioniert.
Und es gibt Beispiele mit komplexen Zahlen, bei denen nichts funktioniert. Bekannte und auswendig gelernte Methoden helfen nicht.
Nehmen wir zum Beispiel diese unschuldig aussehende Potenzierung:
{( 1+2i )^8}Auf dem bereits oft beschrittenen Weg möchtest du die Zahl 
in trigonometrischer Form schreiben und dann mit der entsprechenden Formel in die achte Potenz heben.
Also berechnest du das Modul:
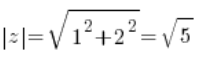
Dann berechnest du den Sinus und Kosinus des Hauptarguments:
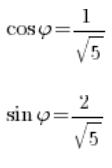
Die Vorzeichen bei Kosinus und Sinus sind positiv, also liegt der Winkel im ersten Quadranten, aber hier endet dein Glück.
Leider findest du die Werte für Sinus und Kosinus: 
und 
nicht in der Tabelle der grundlegenden trigonometrischen Werte. Kein Wunder – der Winkel 
ist weder 0, 30, 45, 60 noch 90 Grad.
Also haben wir ein PROBLEM.
Was kann man tun?
Situationen, in denen eine Zahl, die potenziert wird, nicht so leicht in trigonometrische Form umgewandelt werden kann, können passieren. Leider.
Aber niemand hat gesagt, dass dieselbe Zahl, die zum QUADRAT erhoben wird (zum Beispiel), weiterhin „nicht umwandelbar“ sein wird.
Also versuch es mal so:
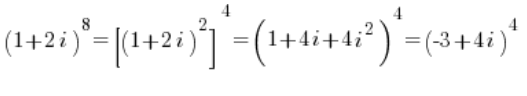
Statt die Zahl: 
in trigonometrische Form zu bringen, wandelst du also die Zahl 
…
Leider mit ebenso schlechten Ergebnissen, denn obwohl das Modul schön und rund ist, lassen sich die Werte für Sinus und Kosinus immer noch nicht aus der Tabelle ablesen.
Was jetzt?
Wiederhole das Manöver 🙂
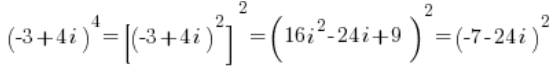
Und hier, statt sich mit der trigonometrischen Form abzumühen, quadriere sie einfach in der algebraischen Form:
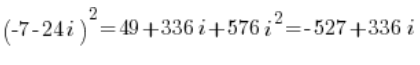
Auf diese Weise haben wir, ohne wirklich die trigonometrische Form anzufassen (weil es nicht ging), eine relativ hohe Potenz der komplexen Zahl ziemlich – ich denke immer noch schmerzlos – berechnet:
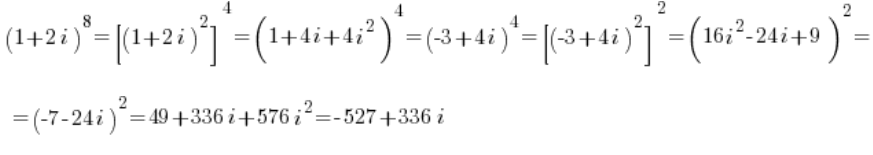
Natürlich. Das funktioniert nicht immer. Aber manchmal kann es helfen, oder? 🙂
