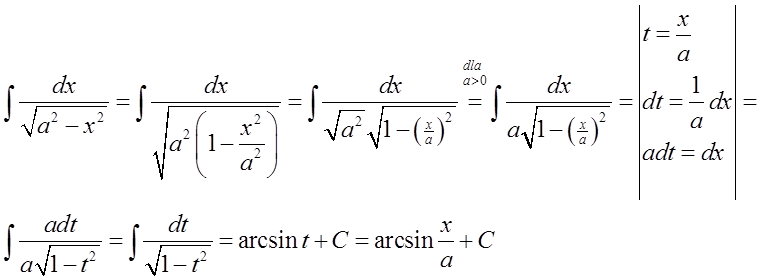Verbotene Formeln für unbestimmte Integrale – Ableitung der Formeln

---

Professoren an Universitäten haben ihre eigenen Anforderungen. Viele von ihnen – natürlich zum Wohle ihrer Studenten – zögern nicht, die Regeln, nach denen Aufgaben gelöst werden sollen, sehr detailliert festzulegen.

Ein Benutzer meines Kurses über unbestimmte Integrale schrieb mir auf GG:

Ich habe eine Bitte, könnten Sie auf Ihrer Facebook-Seite oder Ihrem Blog zeigen, wie Integrale in Ihren Formeln auf das Blattformat gebracht werden? Ich meine die Formeln Nr.: 5, 9, 10, 13, 14, 15, 16. Leider hat unsere Professorin uns mitgeteilt, dass nur die einfachsten verwendet werden dürfen, die komplexeren, die ich erwähnt habe, müssen wir selbst in die angegebene Form zerlegen. Ich denke, viele Leute wären Ihnen dafür dankbar 🙂

Es geht um das Blatt mit den Formeln, das dem Kurs beigefügt ist:

Formeln für unbestimmte Integrale

Und zwar konkret um diese Formeln:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

 

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

 

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

 

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

 

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

 

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

 

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

 

Wenn nicht diese, dann andere

Ja, es stimmt, Professoren verlangen oft, dass bestimmte Formeln verwendet werden und andere nicht. Oder gar keine bestimmten Formeln. Oder sie verlangen, dass wir Formeln verwenden, die wir nicht mögen.

Die einzige vernünftige Lösung in solchen Situationen ist natürlich vollständige Unterwerfung. Im Prüfungsraum ist der Professor das Gesetz, und es hat keinen Sinn, sich später bei Freunden zu beschweren, dass der Professor das Kolloquium nicht bestanden hat, obwohl „er sollte“.

Stattdessen werde ich mir die genannten Formeln Punkt für Punkt ansehen und zeigen, wie man in jedem Fall individuell vorgeht (leider kann man sie nicht mit einer gemeinsamen Regel „umfassen“). „Vorgehen“ bedeutet, Integrale, die die Verwendung dieser Formel erfordern, ohne diese Formel zu lösen – aber mit einer weniger allgemeinen Formel oder durch Substitution oder rationale Methode zu lösen.

Also der Reihe nach:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

Bei dieser Formel weiß ich eigentlich nicht, worum es geht, sie ergibt sich doch direkt aus der Umkehrung der Ableitungsformel:

{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a

Hier zeige ich also nicht vollständige Unterwerfung gegenüber dem Professor, sondern bitte um Erklärung, wie ich bitte \int{{{3}^{x}}dx} ohne Verwendung der Formel \int{{{a}^{x}}dx} berechnen soll.

Wenn jemand auf eine interessante Idee kommt, bitte ich darum, sie in den Kommentaren unter dem Beitrag mit der Menschheit zu teilen.

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

Gut, zurück zum Spiel.

Diese Formel ergibt sich nicht direkt aus der Umkehrung einer Ableitungsformel.

Wenn wir vereinbaren, dass wir sie nicht kennen, können wir das Integral \int{tgxdx} durch Substitution berechnen:

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

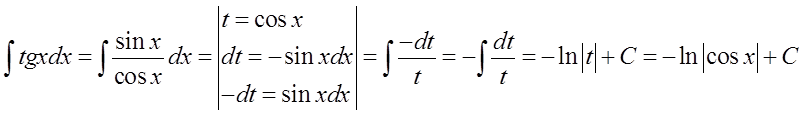
Hier analog zum vorherigen:

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

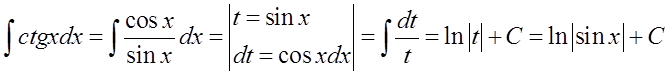
Diese Formel ist die allgemeine Form der Formel:

\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} oder: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}

Dem Professor geht es darum, die Formel zu verwenden: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} (die sich aus einer einfachen Umkehrung der Ableitungsformel ergibt) und nicht die Formel: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C} (die bereits eine „verarbeitete“ Formel ist).

Wir tun dies wie folgt (durch Umformung und Substitution):

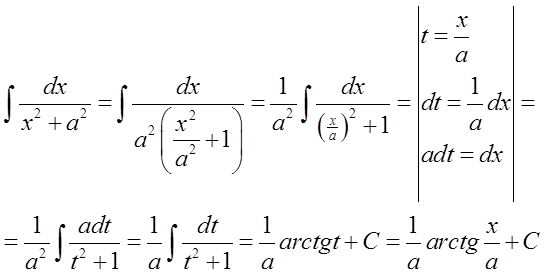
In einem konkreten Beispiel könnte das so aussehen:

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

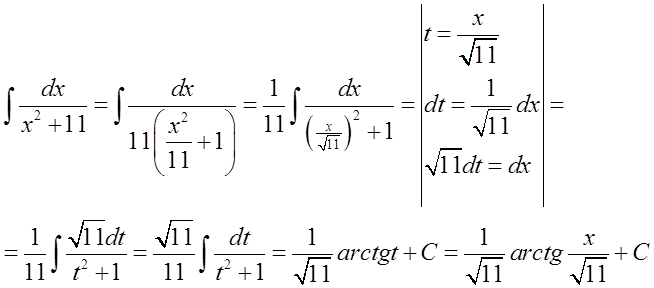
Diese Formel unterscheidet sich von der vorherigen, hier geht es nicht darum, eine Formel zu verwenden, bei der anstelle von ‘a’ ‘1’ steht (eine solche Formel gibt es nicht). Eine Alternative zur Verwendung dieser Formel ist hier die Zerlegung in Partialbrüche wie bei rationalen Integralen (ich habe gezeigt, wie das in Lektion 5 des Kurses über unbestimmte Integrale gemacht wird).

Tatsächlich, \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)} und kann weiter in Partialbrüche zerlegt werden. Zum Beispiel:

\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}

Dann multiplizieren wir mit \left( x-3 \right)\left( x+3 \right), berechnen die Konstanten A, B durch Vergleich der Polynome und alles wie in Lektion 5 des Kurses gezeigt.

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

Hier wieder die allgemeine Formel: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C} muss in die spezielle Formel: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C} umgewandelt werden.

Wir machen das ähnlich wie bei Formel 13):

In einem konkreten Beispiel könnte das so aussehen:

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

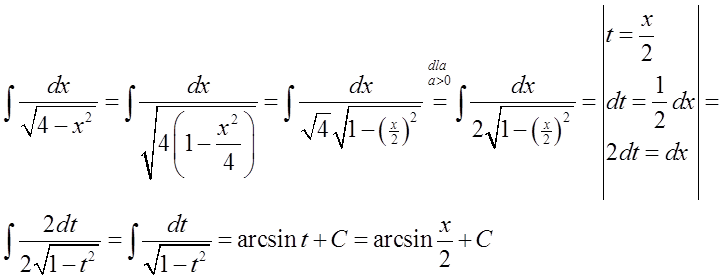
Die Angelegenheit ist komplizierter und erfordert die Verwendung sogenannter „hyperbolischer Substitutionen“ (hyperbolischer Sinus und Kosinus). Dieses Thema lasse ich in diesem Beitrag aus, werde aber bald sicher darüber schreiben.

Das sind die Formeln, nach denen der Benutzer gefragt hat, und ich füge hinzu, dass die von mir zur Liste der grundlegenden Formeln hinzugefügten Formeln:

\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+C

Durch einfache Substitution abgeleitet werden: t=ax

Also zum Beispiel, wenn wir das Integral haben: \int{{{e}^{-x}}dx} und NICHT (aufgrund der Vorlieben des Professors) die Formel \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C verwenden können, verwenden wir die Substitution t=-x und rechnen ruhig weiter.