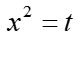In unbestimmten rationalen Integralen, wie wir wissen, muss oft der Nenner der zu integrierenden Funktion in Faktoren zerlegt und weiter in einfache Brüche zerlegt werden.
Aber die Faktorisierung selbst kann oft problematisch sein.
Typische Situationen
Bei einfachen Situationen wie:
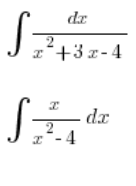
Kommen wir klar:
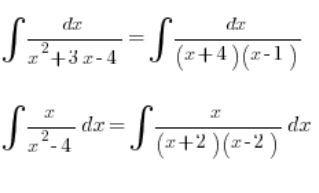
Wenn der Nenner ein passend „arrangiertes” Polynom dritten Grades ist, schaffen wir das auch noch:
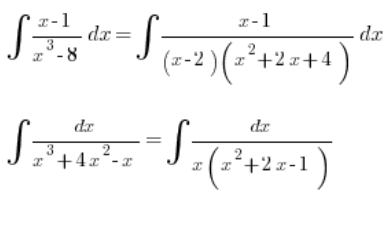
Nenner mit einem unfreundlichen Polynom dritten Grades
Das Problem beginnt, wenn der Nenner ein unfreundlicheres Polynom dritten Grades zur Faktorisierung hat, zum Beispiel:
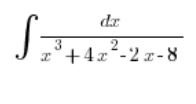
Tiefer Atemzug.
Panikkontrolle.
Solche Sachen (Faktorisierung dieses Typs von Polynom) wurden schon in der Oberschule gemacht und zwar auf grundlegendem Niveau.
Man braucht nur einen cleveren Trick:
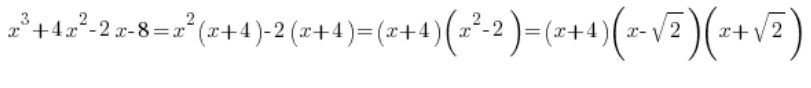
Erinnerst du dich? Natürlich…
Also können wir das Polynom im Nenner faktorisieren:
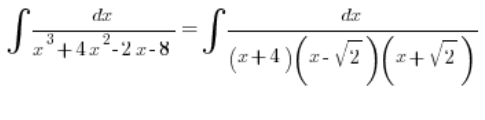
Und dann fröhlich in drei einfache Brüche zerlegen, wie es die Regeln vorschreiben.
Noch schwierigere Faktorisierung
Und was ist mit so einer Situation? Erinnerst du dich aus der Oberschule (das ist eher erweitertes Niveau)?
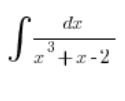
Hier war es ein bisschen schlimmer. Der mittlere Term musste in zwei Teile zerlegt werden:
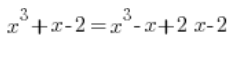
Und dann wie gewohnt weiter:
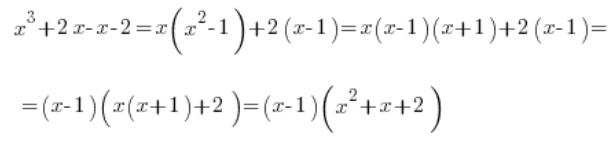
Das Integral sollte also geschrieben werden als:
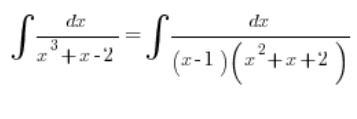
Und ruhig weiterrechnen.
Methoden zur Faktorisierung des Nenners in rationalen Integralen
Generell, erinnere dich in rationalen Integralen, dass wenn die Faktorisierung des Polynoms erforderlich ist, alle Tricks aus der Oberschule erlaubt sind, und das könnten zum Beispiel sein:
- Faktorisierung einiger Polynome vierten Grades durch eine Hilfssubstitution

- Blind nach einer Wurzel suchen und das Polynom teilen, um seinen Grad zu senken
Natürlich sprechen wir jetzt nur über die schwierigeren unbestimmten rationalen Integrale, die in vielen (den meisten?) Universitäten gar nicht erst eingeführt werden!