Euler-Substitution der ersten Art (für a>0) – Wiederholung
Im vorherigen Beitrag:
Euler-Substitution der ersten Art
haben wir uns mit Integralen vom Typ:
 beschäftigt,
beschäftigt,
bei denen a>0.
Wir haben auch ein Beispielintegral gelöst, das diese Bedingung erfüllt, nämlich
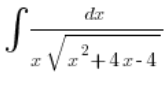
Aber was, wenn ![]() im Trinom negativ ist (den Fall a=0 können wir vernachlässigen, da es dann kein quadratisches Trinom mehr wäre und das Integral durch einfachere Substitution gelöst werden kann
im Trinom negativ ist (den Fall a=0 können wir vernachlässigen, da es dann kein quadratisches Trinom mehr wäre und das Integral durch einfachere Substitution gelöst werden kann ![]() als die Euler-Substitution) ?
als die Euler-Substitution) ?
Dann kann uns der zweite Typ der Euler-Substitution helfen (oder auch nicht…):
Euler-Substitution der zweiten Art (für c>0)
Wir haben ein Integral vom Typ:
 ,
,
bei dem c>0 ist, verwenden wir eine Substitution des Typs:
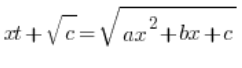 ,
,
das wir erneut auf beiden Seiten quadrieren, wobei diesmal die Terme mit ![]() sich kürzen und dann müssen wir beide Seiten durch
sich kürzen und dann müssen wir beide Seiten durch ![]() teilen, um eine lineare Abhängigkeit zu erhalten, aus der wir mit der Variable
teilen, um eine lineare Abhängigkeit zu erhalten, aus der wir mit der Variable ![]() in der Reihenfolge lösen:
in der Reihenfolge lösen:
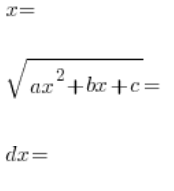
Wir setzen das alles in das Integral ein:

und erhalten erneut ein rationales Integral, das – wie ich wiederhole – in der Regel mühsam ist.
Lass uns also mit einem Beispiel beginnen.
Beispiel
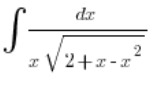
Im quadratischen Trinom ist die Reihenfolge der Terme etwas verändert, aber es ist klar, dass ![]() . Das bedeutet, dass
. Das bedeutet, dass ![]() nicht größer ist als
nicht größer ist als ![]() (wir verwenden also nicht die erste Art der Euler-Substitution), aber c>0 (also verwenden wir die zweite Art).
(wir verwenden also nicht die erste Art der Euler-Substitution), aber c>0 (also verwenden wir die zweite Art).
Wir substituieren also:
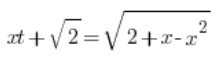
Wir quadrieren beide Seiten:
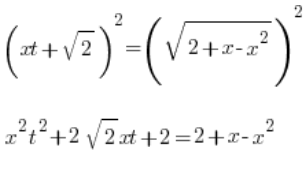
Der Term 2 kürzt sich (wie es sein soll):
![]()
Und jetzt etwas, das in der ersten Art der Substitution nicht vorkam, wir teilen beide Seiten durch x:
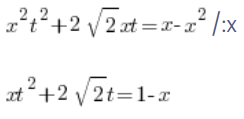
Als nächstes lösen wir für x:
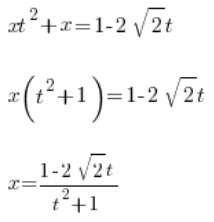
Wir haben x in Bezug auf die Variable t gelöst. Jetzt lösen wir für 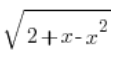 . Anfangs hatten wir die Substitution:
. Anfangs hatten wir die Substitution:
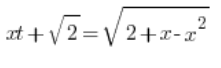
![]() ist bereits gelöst, also setzen wir es einfach ein:
ist bereits gelöst, also setzen wir es einfach ein:
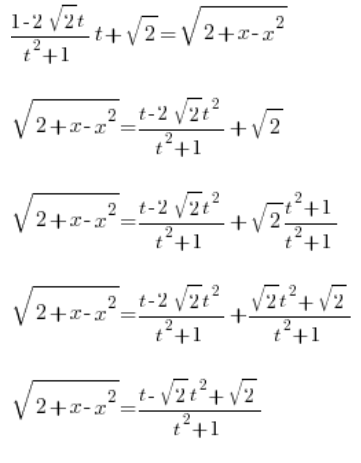
Wir müssen nur noch ![]() lösen. Wir berechnen es, indem wir die Ableitung von
lösen. Wir berechnen es, indem wir die Ableitung von ![]() nehmen:
nehmen:
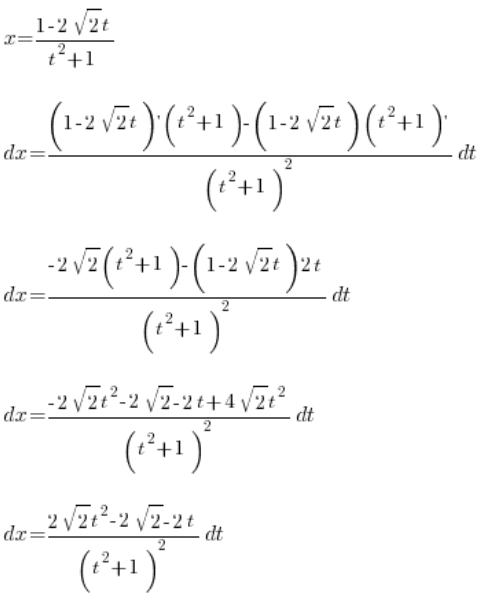
Wir haben also gelöst:
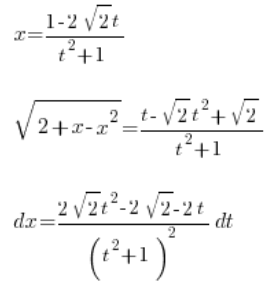
, alles unter Verwendung der Variable ![]() . Wir nehmen das Integral:
. Wir nehmen das Integral:
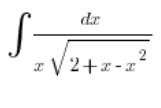
und substituieren:
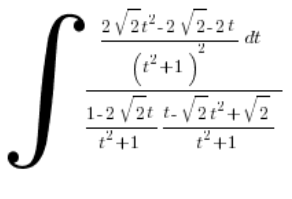
Lass uns aufräumen:
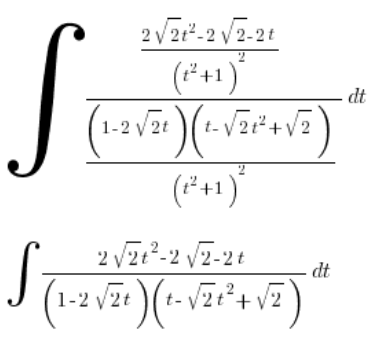
Zurück zur Substitution:
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+CWir müssen noch von t zu x zurückkehren. Unsere Euler-Substitution war
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}Daraus ergibt sich
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}Somit ist unsere Lösung
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+CWas ist mit anderen Fällen?
Wir wissen, dass wenn im Integral:

- a>0 – wir verwenden die erste Art der Substitution
- c>0 – wir verwenden die zweite Art der Substitution
Was aber, wenn weder ![]() noch
noch ![]() größer als null sind? Das besprechen wir im nächsten Beitrag, in dem ich die dritte Art der Euler-Substitution behandle und zeige, dass das Thema damit abgeschlossen ist, d.h. für jedes Integral vom Typ:
größer als null sind? Das besprechen wir im nächsten Beitrag, in dem ich die dritte Art der Euler-Substitution behandle und zeige, dass das Thema damit abgeschlossen ist, d.h. für jedes Integral vom Typ:

…werden wir eine der drei Substitutionsarten wählen.

