Es gibt Zeiten im Leben, in denen das Integrationsgebiet in einem Doppelintegral eine Ellipse ist….
Was dann?
Elliptische Koordinaten
Eine elegante Methode zur Lösung besteht meistens darin, die sogenannten elliptischen Koordinaten zu verwenden. Das ist etwas Ähnliches wie Polarkoordinaten, die Arbeitsweise ist ganz ähnlich, nur setzt man andere Dinge für x und y ein und der Jakobideterminant ist anders. Die Interpretation von ‚r‘ ist auch anders. Also, um es zusammenzufassen: Wenn du weißt, wie man zu Polarkoordinaten wechselt (was meistens dann der Fall ist, wenn das Integrationsgebiet ein Kreis ist), dann wirst du auch die elliptischen Koordinaten problemlos verstehen.
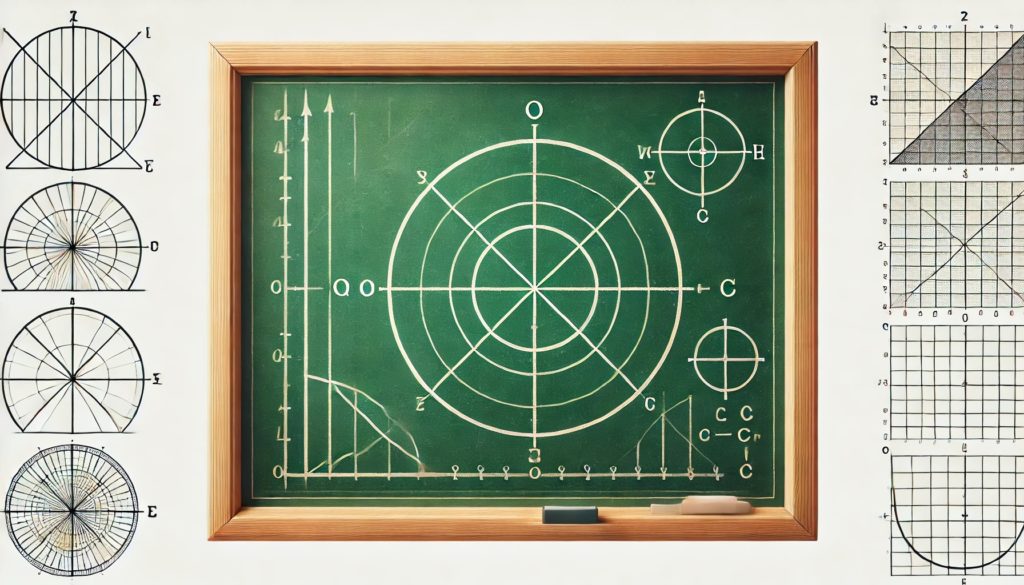
Also haben wir das Integral: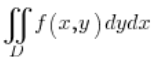 
und das Integrationsgebiet, das durch eine Ellipse mit dem Mittelpunkt im Ursprung begrenzt ist, deren Gleichung lautet: 
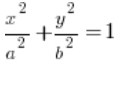. Stellen wir sicher, dass die rechte Seite der Ellipsengleichung auf jeden Fall 1 ist, okay? Wenn dort zum Beispiel eine 9 steht, kannst du sie leicht zu einer 1 machen, indem du beide Seiten der Gleichung durch 9 teilst.
Das gezeichnete Integrationsgebiet sieht so aus:
Was a und b bedeuten, ist auf der Zeichnung zu sehen. Man muss aufpassen, denn wenn im Nenner der Ellipsengleichung unter 
zum Beispiel 9 steht, bedeutet das, dass 
, aus offensichtlichen Gründen, richtig?
Nun, mit einer solchen „sauberen“ Situation wechseln wir zu elliptischen Koordinaten, indem wir ersetzen:
Bedeutung der Variablen in elliptischen Koordinaten
Der Winkel 
bedeutet genau das gleiche wie bei Polarkoordinaten, und 
bedeutet etwas anderes. Bei grundlegenden Aufgaben mit einer Ellipse, die durch eine schöne Gleichung gegeben ist 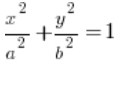, nimm einfach an, dass von Null bis Eins reicht (in komplexeren Fällen setze und in die Ellipsengleichung ein und berechne die obere Grenze von r).
Jakobi
Der Jakobi in elliptischen Koordinaten ist gleich 
.
Wenn wir uns an den Jakobi erinnern, wechseln wir also zum Integral in elliptischen Koordinaten:
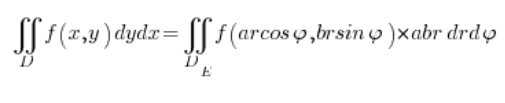
wobei die Variablen und begrenzt sind: im Bereich von Null bis Eins und je nachdem, ob wir über die gesamte Ellipse, die Hälfte oder z.B. ein Viertel sprechen – genau wie bei Polarkoordinaten.
Einfach nehmen und rechnen.
Beispiel
Berechne das Integral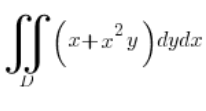 
, wobei D die Ellipse mit der Gleichung: 
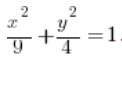ist.
Nach dem obigen Schema setzen wir ein:
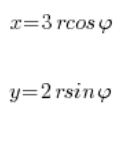
Wir nehmen das Integrationsgebiet:
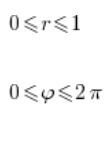
Und berechnen das Integral:
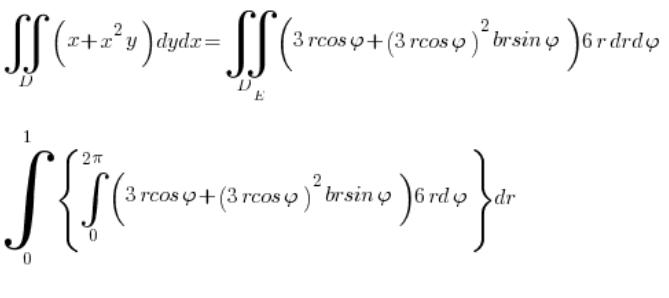
Was natürlich jetzt nur noch Formsache ist 🙂
