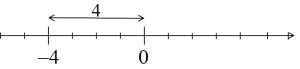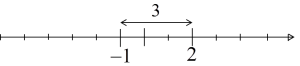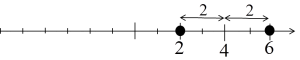Es befinden sich momentan keine Produkte im Warenkorb.
Krystian Karczyński- 15 Juli 2024
- Komentarz 0
Wenn du schon eine Weile Mathematik an der Universität studierst, hast du sicherlich bemerkt, dass die meisten der in der Schule durchgenommenen Materialien dir an der Universität nicht direkt nützlich sind. Wenn du gerade erst anfängst – achte darauf.
Was bedeutet „direkt“?
Ich sage „direkt“, weil natürlich jeder Tropfen deines mathematischen Schweißes in der Schule nicht verschwendet wird und für dich gezählt wird. Ich spreche von der Übung im abstrakten Denken, der Fähigkeit, sich auf ein Problem zu konzentrieren, und so weiter.
Doch ehrlich gesagt, wirst du viele der in der Schule durchgenommenen Mathematikbereiche nicht mehr brauchen, nicht einmal, um einen Blick darauf zu werfen und etwas zu wiederholen.
Aber es gibt Ausnahmen.
Es gibt Dinge, die in der Schule durchgenommen werden, ohne deren Kenntnis du an der Universität nicht weit kommst.
Zu Beginn des akademischen Jahres lohnt es sich, sie zu wiederholen oder einfach zu lernen. Dadurch ebnest du dir den Weg zu weiteren, neuen Themen. Wenn sie nicht durchgenommen werden, werden sie dich ständig stören, wie ein Dorn im Schuh, und deinen Fortschritt behindern (oder sogar unmöglich machen).
Es werden keine großen Mathematikbereiche sein, sondern meist kleine Details, kleine Bausteine, ohne die das ganze Gebäude einstürzen kann.
Definition der Grenze
Nehmen wir zum Beispiel die Definition der Grenze einer Folge, der du sehr schnell begegnen wirst:
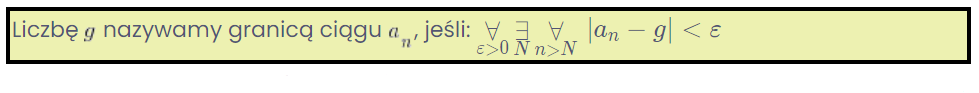
Verstehst du diese seltsamen Zeichen links? Und diesen absoluten Wert rechts? Nicht viel?
Und doch sollte die Kenntnis der Quantoren (diese Kreaturen links: 
) und der geometrischen Interpretation des absoluten Werts (rechts) aus der Schule ausreichen, um diese Definition zu verstehen oder zumindest richtig zu lesen…
Aber lasst uns nicht jammern, sondern an die Arbeit gehen. In diesem und den nächsten Beiträgen zeige ich dir einige Details, deren Verständnis das Studium an der Universität erheblich erleichtern wird.
Wir beginnen mit…
1. Geometrische Interpretation des absoluten Werts (als Entfernung)
Im Großen und Ganzen wissen wir alle, worum es bei diesem absoluten Wert geht. Niemand hat ein Problem damit, dass:
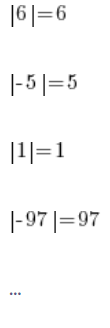
Die Operation des absoluten Werts gibt einfach die gleiche Zahl zurück, und wenn sie negativ ist, ändert sie ihr Vorzeichen auf Plus.
Was würde sie geometrisch bedeuten? Auf der Zahlengerade? Einfach die Entfernung einer Zahl von Null. Zum Beispiel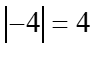 
und in der Tat ist die Entfernung der Zahl 
von Null zweifellos 4:
Wir werden weiter diesem Pfad folgen und den absoluten Wert genau als Entfernung verstehen.
Lass uns noch eine Sache bemerken:
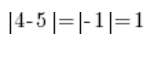
Und dass auf der Zahlengerade:
…dass die Entfernung zwischen 4 und 5 genau dem Zahlenwert der DIFFERENZ (Subtraktion) von 4 und 5 entspricht, unabhängig davon, was wir von was subtrahieren, weil:
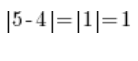
Ähnlich, wenn wir die Zahlen 3 und 8 subtrahieren und den absoluten Wert des Ergebnisses berechnen, erhalten wir genau die Entfernung auf der Zahlengerade zwischen den Zahlen 3 und 8 (es wird 5 sein).
Dies funktioniert auch bei negativen Zahlen, zum Beispiel -1 und 2:
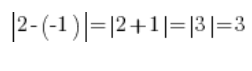
…das ist genau die Entfernung zwischen den Zahlen -1 und 2:
Du kannst auch ein bisschen damit selbst experimentieren. Wenn du ein Lehrbuch aus der Schule hast, ermutige ich dich sehr, eine Stunde lang dieses Thema zu vertiefen und ein wenig zu bearbeiten.
Wir können eine allgemeine Regel formulieren:
Der absolute Wert der Differenz (Subtraktion) zweier Zahlen: 
und 
entspricht der Entfernung dieser Zahlen voneinander.
Wie können wir also zum Beispiel eine solche Gleichung entschlüsseln:
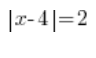
Wir wissen, dass der Teil 
die Entfernung des Unbekannten x von 4 bedeutet, und auf der rechten Seite der Gleichung wissen wir, dass diese Entfernung gleich 2 sein sollte.
Daher wird die Lösung der Gleichung Zahlen sein, deren Entfernung von 4 gleich 2 ist, also die Zahlen 2 und 6:
Und jetzt nehmen wir diese Ungleichung:
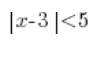
Ihre linke Seite ist die Entfernung x von der Zahl 3, und weiter gelesen erhalten wir die Information, dass diese Entfernung kleiner als 5 sein sollte. Diesmal wird die Lösung dieser Ungleichung nicht nur zwei Zahlen sein, sondern viele mehr – alle Zahlen, deren Entfernung von 3 kleiner als 5 ist. Auf der Achse würde es so aussehen:
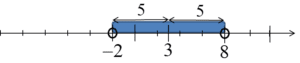
…das bedeutet, es wären alle Zahlen von -2 bis 8, also das Intervall: 
. Die Entfernung jeder solchen Zahl von 3 ist kleiner als 5.
Dieses Intervall kann auch als ein bestimmtes Umfeld des Punktes 3 bezeichnet werden (ein wichtiger Begriff, der an der Universität oft verwendet wird).
Durch die gleiche Überlegung kannst du herausfinden, welche Zahlen die Ungleichung erfüllen: 
…
Dies ist jedoch nicht mein Ziel (du hattest das schon in der Schule, oder 🙂 ?).
Es ist jedoch gut, den absoluten Wert als Entfernung zu verstehen, da er in vielen mathematischen Definitionen vorkommt, die du an der Universität treffen wirst. Und dann ist es gut, sofort zu wissen, „worum es geht“.
Zum Beispiel nehmen wir die bereits erwähnte Grenzwert einer Folge:
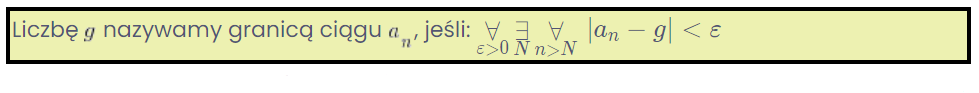
Konzentrieren wir uns vorerst auf die rechte Seite der Formel. Lassen wir die seltsamen Symbole auf der linken Seite für den nächsten Beitrag.
Welche Lesart trifft mehr ins Herz und ist besser verständlich:
„der absolute Wert der Differenz zwischen 
und 
muss kleiner sein als 
“
oder:
„die Entfernung zwischen und muss kleiner sein als “
?
Formal sind beide Weisen, die Definition zu formulieren, gleichwertig, aber die zweite ist einfacher und konzentriert sich auf das Wesentliche, ohne sich unnötig auf einige arithmetische Operationen wie Differenz zu zerstreuen.
Das Verständnis des absoluten Werts als Entfernung wird es dir viel leichter machen, viele – scheinbar komplizierte – mathematische Theoreme und Definitionen an der Universität zu verstehen.
Was kommt als nächstes?
Im nächsten Beitrag werde ich mich mit diesen seltsamen Symbolen beschäftigen: 
und 
, damit wir unsere Beispieldefinition vollständig verstehen können.
