Definition des Rangs einer Matrix und was daraus folgt
Angenommen, wir haben den Rang einer Matrix definiert als: „Anzahl der linear unabhängigen Zeilen und Spalten in einer Matrix“. Welche Eigenschaften des Rangs ergeben sich bereits aus dieser Definition?
Zunächst ist klar, dass der Rang einer Matrix gleich: 1, oder 4, oder manchmal 0 sein kann. Aber er wird sicher nicht gleich: -4, oder ![]() sein.
sein.
Okay, ist das alles?
Aber ist das alles, was man daraus ableiten kann? Nehmen wir zum Beispiel die folgende Matrix:
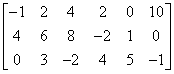
Diese Matrix hat 3 Zeilen und 6 Spalten.
Fragen wir uns, was der Rang dieser Matrix sein kann? Kann er gleich 7 sein? Es ist klar, dass das nicht möglich ist, denn wenn der Rang einer Matrix „die Anzahl der linear unabhängigen Zeilen und Spalten“ ist, kann er in diesem Fall nicht 7 sein, da diese Matrix nicht so viele Zeilen oder Spalten hat!
Nun eine schwierigere Frage… Kann der Rang gleich 6 sein? Die Matrix hat ja 6 Spalten…
Die Antwort lautet: nein. 6 müsste „die Anzahl der linear unabhängigen Zeilen und Spalten“ sein. 6 kann die Anzahl der linear unabhängigen Spalten sein (weil es 6 Spalten gibt), aber es kann nicht die Anzahl der linear unabhängigen Zeilen sein (weil es nur 3 Zeilen gibt). Und es sollte die Anzahl der linear unabhängigen „Zeilen und Spalten“ sein.
Es ist also offensichtlich, dass der Rang dieser Matrix maximal 3 sein kann.
Wir kommen hier zu einer nützlichen Eigenschaft:
rang(A) <= min(Anzahl der Zeilen der Matrix, Anzahl der Spalten der Matrix)
Daher kann man durch das Betrachten einer Matrix sofort deren maximalen Rang erkennen – was manchmal sehr nützlich sein kann.
Um ihn genauer zu berechnen, musst du jedoch geeignete Methoden anwenden – ich zeige sie in meinem Matrix-Kurs in Lektion 5, willkommen!


