Der Rang einer Matrix mit einem Parameter
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Nehmen wir an, wir sollen den Rang der Matrix berechnen:
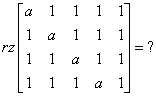
Lösung
Es gibt verschiedene Methoden, dies zu lösen, und wahrscheinlich ist die schnellste, die fünfte Spalte mit -1 zu multiplizieren und zu den ersten vier Spalten hinzuzufügen, wodurch sich ergibt:
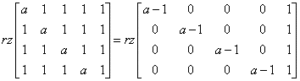Nun nehmen wir die Determinante der 4. Ordnung der Matrix:
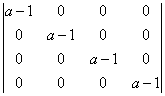Eine Determinante, bei der alle Elemente außer der Hauptdiagonale null sind, ist gleich dem Produkt der Elemente auf der Hauptdiagonale (ich werde das irgendwann mal beweisen 🙂 ), also:
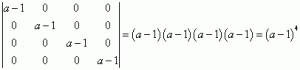Diese Determinante ist für alle a, die nicht gleich 1 sind, ungleich null. Daher ist für solche a der Rang unserer Matrix, den wir berechnen müssen, 4 (weil man daraus einen nicht null 4. Ordnung Minor extrahieren kann, einen größeren jedoch nicht).
Und was ist mit dem Fall, in dem 
. Dann erhalten wir den Rang der Matrix (ersetzen wir a durch 1):
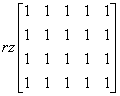Und dieser Rang ist 1 (man kann z.B. wieder die fünfte Spalte auf die anderen anwenden und die null Spalten eliminieren).
Also, für a ungleich 1 ist der Rang der Matrix 4, und für a gleich 1 ist der Rang der Matrix 1.
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
