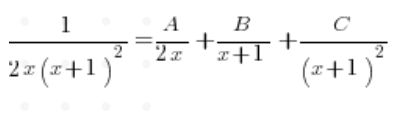Delta gleich null in rationalen unbestimmten Integralen

Zerlegung eines quadratischen Trinomials

In rationalen unbestimmten Integralen ist es oft notwendig, ein quadratisches Trinomial zu zerlegen: 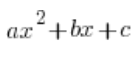. Wir machen das natürlich mit der Formel: 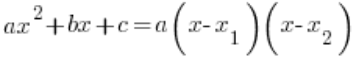, die funktioniert, wenn .

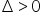Rationale Integrale und Delta gleich 0

Wie sieht jedoch dieser Binomial aus, wenn Delta genau 0 ist? Zum Beispiel, wie sieht die Faktorisierung aus: ?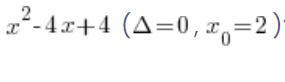

Sieht es so aus:  ?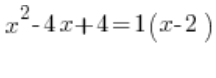

Natürlich nicht… Aus der Schule erinnern wir uns, dass wenn , dann haben wir tatsächlich eine Wurzel, aber es ist eine doppelte. In unserem Beispiel können wir also sagen: , was bedeutet, dass das quadratische Trinom auf diese Weise zerlegt wird:

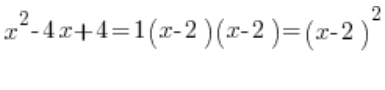
Das hat erhebliche Folgen für rationale unbestimmte Integrale, wenn sie in einfache Brüche zerlegt werden.

Beispiel

Wir nehmen ein Beispiel:

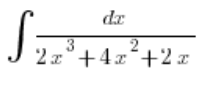
Wir zerlegen den Bruch ohne das Integral und schreiben:

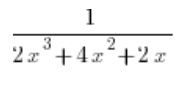
Wir nehmen im Nenner x vor die Klammer:

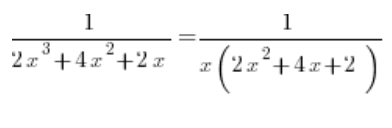
Aus dem quadratischen Trinomial im Nenner berechnen wir das Delta, welches 0 ergibt, und die Wurzel ist (-1). Zerlegen wir es in Faktoren, erhalten wir:

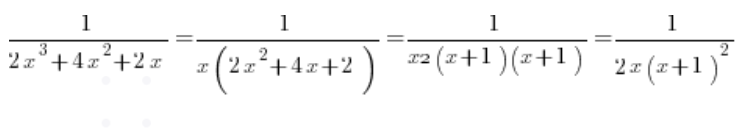
Und zerlegt in einfache Brüche: