Beim Berechnen von Quadratwurzeln in kartesischer (oder: algebraischer) Form in meinem Kurs über komplexe Zahlen habe ich eine Methode gezeigt, die darin besteht, eine dritte Gleichung zu den bereits vorhandenen zwei Gleichungen hinzuzufügen, was die weiteren Berechnungen erheblich vereinfacht und verkürzt.
Ich habe diese Methode gezeigt, aber nicht begründet.
Und genau zu diesem Anlass habe ich kürzlich eine E-Mail mit folgendem Inhalt erhalten:
Hallo
Könnten Sie erklären, warum wir die Methode verwenden können, indem wir eine dritte Gleichung hinzufügen, wenn wir die Quadratwurzel einer komplexen Zahl berechnen?
x^2 + y^2 = das Modul der Zahl, deren Wurzel wir berechnen
Das ist eine SEHR gute Frage und wirklich gesegnet in der Mathematik sind diejenigen, die den Professoren nicht einfach glauben, sondern immer fragen: „Woher kommt das?“ 🙂
Begründung
Nun bleibt mir nichts anderes übrig, als diese Methode auf eine der möglichen Weisen zu begründen:
Nach den ersten Schritten bei der Berechnung der Quadratwurzel haben wir die Situation:
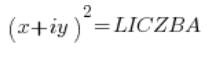
Da die Zahlen (ich werde nicht jedes Mal „komplexe Zahlen“ schreiben) auf der linken und rechten Seite gleich sind, müssen auch ihre Module gleich sein (anders herum gilt das nicht, aber das ist nicht wichtig), also:
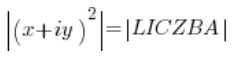
Eine Zahl im Quadrat ist eine Zahl mal sich selbst, also:
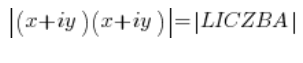
Das Modul einer komplexen Zahl hat die Eigenschaft: 
, also können wir auf der linken Seite schreiben:
… und beim Berechnen der Module auf der linken Seite haben wir:
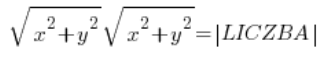
das heißt:
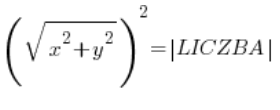
das heißt:
das heißt:
BINGO
Danke für die gute Frage!
