Zakazane wzory na całki nieoznaczone – wyprowadzenie wzorów

Znak zakazuProfesorzy na uczelniach mają swoje wymagania. Wielu z nich – dla dobra swoich studentów oczywiście – nie cofnie się przed bardzo szczegółowym określeniem reguł, na jakich mają być rozwiązywane zadania.

Użytkownik mojego Kursu Całek Nieoznaczonych napisał mi na GG tak:

mam prośbę, czy mógłby Pan na swoim FB lub blogu pokazać jak całki w Pana wzorach są doprowadzane do postaci z kartki ? Chodzi mi o wzory nr: 5,9,10,13,14,15,16. Niestety u nas Pani Profesor oznajmiła nam, że tylko te najprostsze można wykorzystywać, te bardziej złożone, które wymieniłem trzeba samemu rozbić do podanej postaci. Myślę, że dużo osób byłoby Panu za to wdzięcznych 🙂

Chodzi o kartkę z wzorami dołączoną do Kursu:

Wzory na całki nieoznaczone

A konkretnie o wzory:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

 

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

 

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

 

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

 

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

 

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

 

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

 

Jak nie tymi, to innymi

Ano tak, to prawda, profesorzy często wymagają, żeby stosować te, a nie inne wzory. Albo żeby nie stosować w ogóle niektórych. Albo żeby stosować te, których nie lubimy stosować.

Jedynym wyjściem dla rozsądnego człowieka oczywiście jest w takich sytuacjach całkowite podporządkowanie się. Na sali egzaminacyjnej wykładowca jest prawem i nie ma sensu wyżalać się później znajomym, że profesor nie zaliczył kolokwium, chociaż „powinien”.

Zamiast tego przyjrzę się wymienionym wzorom punkt po punkcie i pokażę jak sobie radzić w każdym przypadku indywidualnie (niestety nie da się ich „objąć” jakąś wspólną regułą). „Radzić”, to znaczy rozwiązywać całki wymagające użycia tego wzoru bez użycia tego wzoru – za to z użyciem wzoru mniej ogólnego, albo wyprowadzenia całki przez podstawienie, czy wymiernej.

No to po kolei:

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

Z tym wzorem to właściwie nie wiem, o co chodzi, wynika on przecież wprost z odwrócenia wzoru na pochodną:
{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a

Tutaj więc nie okazuję całkowitej uległości profesorowi, tylko proszę o wyjaśnienie, jak mam kurka policzyć \int{{{3}^{x}}dx}nie korzystając z wzoru na \int{{{a}^{x}}dx}.

Jak ktoś wpadnie na jakiś ciekawy pomysł, błagam, żeby podzielił się nim z ludzkością w komentarzach pod postem.

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

Dobra, wracamy do gry.

Ten wzór nie wynika bezpośrednio z odwrócenia żadnego wzoru na pochodną.

Jeżeli umawiamy się, że go nie znamy, całkę \int{tgxdx}możemy policzyć przez podstawienie:

Całka z tgx

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

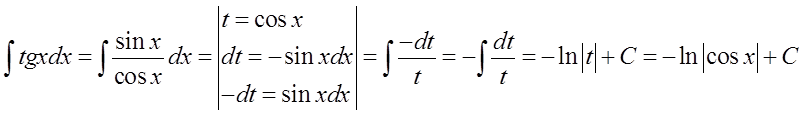
Tutaj analogicznie do poprzedniej:

Całka z ctgx

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

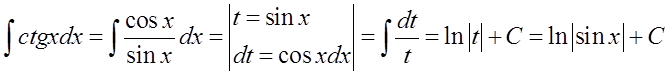
Ten wzór to postać ogólna wzoru:

\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} lub: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}

Panu profesorowi chodzi o to, żeby skorzystać z wzoru: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C}(wynikającego z prostego odwrócenia wzoru na pochodną), a nie korzystać z wzoru: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}(który jest już wzorem w postaci „przetworzonej”).

Robimy to w następujący sposób (przez przekształcenie i podstawienie):

Przekształcenie ogólnego wzoru na całkę z arctgx

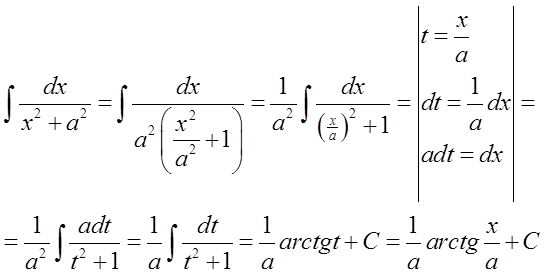
Na konkretnym przykładzie mogło by to wyglądać tak:

Przykład na przekształcenie ogólnego wzoru na całkę na wzór szczególny

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

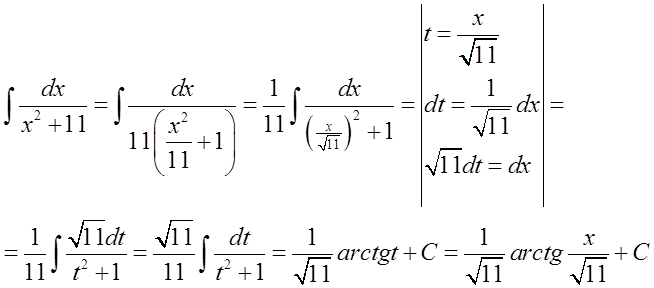
Ten wzór różni się od poprzedniego, nie chodzi tu o to, żeby skorzystać z jakiegoś wzoru, w którym zamiast 'a’ jest '1′ (takiego wzoru nie ma). Alternatywą do skorzystania z tego wzoru jest tu przeprowadzenie rozkładu na ułamki proste jak w całkach wymiernych (pokazałem jak to się robi na Lekcji 5 Kursu Całek Nieoznaczonych).

Faktycznie, \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)}i dalej można rozkładać na ułamki proste. Na przykład:

\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}

Dalej mnożymy przez \left( x-3 \right)\left( x+3 \right), liczymy stałe A, B porównując wielomiany i wszystko tak, jak pokazałem na Lekcji 5 Kursu.

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

Tutaj znowu wzór w postaci ogólnej: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}należy doprowadzić do wzoru w postaci szczególnej: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}.

Robimy to podobnie jak we wzorze 13):

Przejście ze wzoru ogólnego na szczególny we wzorze z arcsin

Na konkretnym przykładzie mogło by to wyglądać tak:

Zastosowanie szczególnej postaci wzoru z arcsin

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

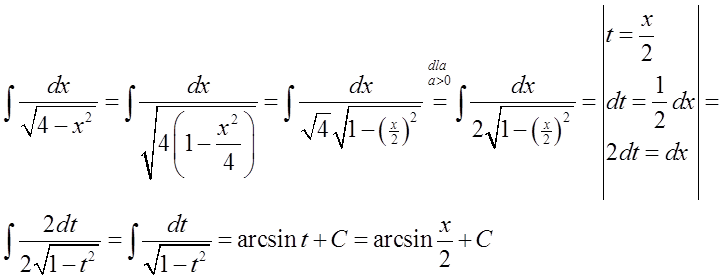
Sprawa jest bardziej skomplikowana, wymaga zastosowania tzw. „podstawień hiperbolicznych” (chodzi o sinusa i cosinusa hiperbolicznego). W tym poście zostawiam ten temat, wkrótce na pewno napiszę o tych podstawieniach.

Tyle wzorów, o które pytał użytkownik, od siebie dodam, że dodane do listy podstawowych wzorów przeze mnie wzory:

\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+C

Wyprowadza się przez proste podstawienie: t=ax

Czyli mając na przykład całkę: \int{{{e}^{-x}}dx}i NIE mogąc skorzystać (ze względu na upodobania profesora) ze wzoru \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C, stosujemy podstawienie t=-xi spokojnie liczymy dalej.

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Related Posts

Zgarnij skrzydła do nauki z eTrapez i Red Bull

Posted on

Skąd mam wiedzieć, co podstawić w całkach nieoznaczonych?

Posted on
Obrazek z video o Kresach

Kresy, ale takie w matematyce (infimum i supremum, inf i sup) – (VIDEO)

Posted on
Trzy kubki i kulka pod jednym

Czy warto było zmienić bramkę w „Idź na całość”? (VIDEO)

Posted on

53 Comments

  1. Mirosław

    Moim zdaniem poprawne obliczenie całki nr 5 jest takie jak poniżej. Funkcję 3^x przedstawiamy jako (e^ln 3)^x i dalej (e^x) ^ln 3. Stosujemy podstawienie e^x=t, dx=dt/t i obliczamy całkę f-cji t^(ln 3 – 1) względem t, otrzymując t^(ln 3)/ln 3 + C. Po przejściu na zmienną x mamy wynik 3^x/ln 3 + C. Pozdrawiam.

    Reply

  2. Robert

    Witam Krystian. Dzięki wielkie za pomoc, bo wczoraj zaliczyłem dzięki Twoim kursom kolokwia z analizy i logiki 🙂 Zawsze byłem humanistą, a w dużej mierze dzięki Twoim lekcjom rozszerzam się na umysł ścisły. Pokazujesz matematykę od tej pięknej strony, której wiele osób nie dostrzega, tonąc w morzu niezrozumiałych zagadnień. Dzięki raz jeszcze!

    Reply

  3. Antoni

    Witam! Próbowałem na różne sposoby, ale nie chce wyjść 🙁 W jaki sposób obliczyć całkę z x+2×3+xdx = ?Pozdrawiam

    Reply

  6. Integral Love

    16. integral fraction numerator d x over denominator square root of x squared plus q end root end fraction

    Udało mi się to zrobić podstawieniem Eulera I rodzaju 😀

    Wezmę a zamiast q, bo tak mam u siebie w obliczeniach i wygodniej będzie mi tu przepisać 🙂

    Najpierw:

    t minus x equals square root of x squared plus a end root t squared minus 2 t x plus x squared equals x squared plus a space t squared minus 2 t x equals a space x equals fraction numerator t squared minus a over denominator 2 t end fraction

    Teraz  square root of x squared plus a end root :

    t minus x equals square root of x squared plus a end root x equals fraction numerator t squared minus a over denominator 2 t end fraction square root of x squared plus a end root equals t minus fraction numerator t squared minus a over denominator 2 t end fraction equals fraction numerator 2 t squared minus \left parenthesis t squared minus a \right parenthesis over denominator 2 t end fraction equals fraction numerator t squared plus a over denominator 2 t end fraction

    Na koniec dx:

    x equals fraction numerator t squared minus a over denominator 2 t end fraction space vertical line fraction numerator d over denominator d t end fraction fraction numerator d x over denominator d t end fraction equals fraction numerator 4 t squared minus 2 t squared plus 2 a over denominator 4 t squared end fraction d x equals fraction numerator t squared plus a over denominator 2 t squared end fraction d t

    I z tego wychodzi taka całka :

    integral fraction numerator 2 t over denominator t squared plus a end fraction times fraction numerator t squared plus a over denominator 2 t squared end fraction d t

    Wszystko ładnie się skraca i zostaje tylko:integral 1 over t d t

    Zanim ją policzę jeszcze wyznaczę t:

    t minus x equals square root of x squared plus a end root t equals x plus square root of x squared plus a end root

    czyli:

    integral 1 over t d t equals ln vertical line t vertical line equals ln vertical line x plus square root of x squared plus a end root vertical line plus C space

    Reply

    1. Integral Love

      aaa ale bałagan :(połączyły mi się wszystkie linijki, mam nadzieję że będzie się dało to zrozumieć 

    1. Krystian Karczyński

      Chodzi o wzór:

      \int{{{x}^{2}}dx}=\frac{1}{3}{{x}^{3}}+C

      …tutaj nie ma co wyprowadzać, ten wzór powstał przez prościutkie odwrócenie wzoru na pochodną:

      {{\left( \frac{1}{3}{{x}^{3}}+C \right)}^{\prime }}={{x}^{2}}

      Z tą „regułą podstawienia liniowego” zupełnie nie wiem, o co chodzi, przykro mi…

  13. Kamil

    Co do 16-tego, wystarczy podstawienie Eulera 😉

    (x^2+c)=x-t

    podnosimy obustronnie do kwadratu, wyznaczamy t ; dx/dt będzie pochodną z otrzymanego wyrażenia itd. itd. 😉

    Reply

  14. Dawid

    do swojego wcześniejszego pytania dołaczam jeszcze pojęcie „kiedy pochodna jest ciagła, kiedy dana funkcja nie ma pochodnej ? Jak to szybko sprawdzic i ładnie wytłumaczy Panu profesorowi?;;)

    Reply

  15. Dawid

    Czy mógłby Pan wyjaśnic pojęcie rózniczkowalnosci, jak zbadac rózniczkowalnosc funkcji? oraz jaka jest róznica miedzy całka oznaczona a nieonzaczona?

    Reply

    1. Krystian Karczyński

      No hmmm… Jasne, tylko, że to baaaardzo szeroki temat. „Różniczkowalność” to liczenie pochodnej, a „zbadać różniczkowalność” to znaczy „zbadać, czy istnieje pochodna”.

      Tutaj znajdziesz moje Wykłady o pochodnych (koniecznie zacznij od początku):

      https://etrapez.pl/blog/pochodne/

      , a tutaj konkretnie o badaniu jej istnienia:

      https://blog.etrapez.pl/pochodne/badanie-istnienia-pochodnej-funkcji/

      Całki nieoznaczone i oznaczone to po prostu zupełnie coś innego, mają inne definicje (chociaż oczywiście wiążą się ze sobą). Tu znajdziesz mój wykład o tym, co to jest całka nieoznaczona:

      https://blog.etrapez.pl/calki-nieoznaczone/calki-nieoznaczone-wprowadzenie/

      a tutaj, co to jest całka oznaczona:

      https://blog.etrapez.pl/calki-oznaczone/calki-oznaczone-definicja/

  16. Agata

    A ja mam problem z takimi przykładami [pmath]int{}{}{(4+x)\sqrt{-x^2-x}dx} [/pmath] [pmath]int{}{}{dx/{e^{2x}+1}}[/pmath] [pmath]int{}{}{\sqrt{arcsinx}dx}[/pmath]

    Reply

    2. Krystian Karczyński

      To może zacznijmy od tej ostatniej. Rozwiązujemy najpierw przez części, a później przez podstawienie.

      \int{arcsin \sqrt{x}}dx=\left| \begin{matrix}
      u=arcsin \sqrt{x}&{v}'=1\\
      {u}'=\frac{1}{2\sqrt{x}\sqrt{1-x}}&v=x
      \end{matrix} \right|=

      =xarcsin \sqrt{x}-\int{\frac{1}{2\sqrt{x}\sqrt{1-x}}\cdot xdx}=xarcsin \sqrt{x}-\frac{1}{2}\int{\frac{\sqrt{x}}{\sqrt{1-x}}dx}=\left| \begin{matrix}
      {{t}^{2}}=1-x\Rightarrow x=1-{{t}^{2}}\\
      2tdt=-dx\\
      dx=-2tdt
      \end{matrix} \right|=

      =xarcsin \sqrt{x}-\frac{1}{2}\int{\frac{\sqrt{1-{{t}^{2}}}}{t}\left( -2tdt \right)}=xarcsin \sqrt{x}+\int{\sqrt{1-{{t}^{2}}}dt}

      Tą całkę można rozwiązać tak jak pokazywałem w moim Kursie Całek Nieoznaczonych (metodą współczynników nieoznaczonych), a można inaczej, przez sprytne podstawienie:

      =xarcsin \sqrt{x}+\int{\sqrt{1-{{t}^{2}}}dt}=\left| \begin{matrix}
      sin u=t\Rightarrow \sqrt{1-{{t}^{2}}}=cos u\\
      cos udu=dt
      \end{matrix} \right|=
      =xarcsin \sqrt{x}+\int{cos ucos udu}=xarcsin \sqrt{x}+\int{{{cos }^{2}}udu}=

      Całkę \int{{{cos }^{2}}udu}pozwolę już sobie przyspieszyć, rozwiązujemy tak jak pokazałem w Kursie i mam:

      =xarcsin \sqrt{x}+\frac{1}{2}u+\frac{1}{2}sin ucos u=xarcsin \sqrt{x}+\frac{1}{2}arcsin t+\frac{1}{2}tsqrt{1-{{t}^{2}}}=

      =xarcsin \sqrt{x}+\frac{1}{2}arcsin \sqrt{1-x}+\frac{1}{2}\sqrt{x}\sqrt{1-x}+C

    3. Agata

      wkradł sie tylko mały błąd, w pochodnej na arcsinx brakuje kwadratu przy x, co zmienia i utrudnia ten przykład niestety

    4. Krystian Karczyński

      To ni błąd, po prostu trochę skróciłem w głowie. Do kwadratu podnoszę nie 'x’, tylko funkcję wewnętrzną arcsin, czyli \sqrt{x}. Rozpisane liczenie pochodnej wyglądało by tak:

      {{\left( arcsin \sqrt{x} \right)}^{\prime }}=\frac{1}{\sqrt{1-{{\left( \sqrt{x} \right)}^{2}}}}\cdot \frac{1}{2\sqrt{x}}=\frac{1}{\sqrt{1-x}}\cdot \frac{1}{2\sqrt{x}}=\frac{1}{2\sqrt{x}\sqrt{1-x}}

    6. Krystian Karczyński

      Co do drugiej całki, trzeba zauważyć, że \int{\frac{dx}{{{e}^{2x}}+1}}=\int{\frac{dx}{{{\left( {{e}^{x}} \right)}^{2}}+1}}i podstawić t={{e}^{x}}:

      \int{\frac{dx}{{{e}^{2x}}+1}}=\int{\frac{dx}{{{\left( {{e}^{x}} \right)}^{2}}+1}}=\left| \begin{matrix}
      &t={{e}^{x}}\\
      &dt={{e}^{x}}dx\\
      &dx=\frac{dt}{{{e}^{x}}}\\
      &dx=\frac{dt}{t}
      \end{matrix} \right|=\int{\frac{\tfrac{dt}{t}}{{{t}^{2}}+1}}=\int{\frac{dt}{t\left( {{t}^{2}}+1 \right)}}

      A dalej już oczywiście wymierna całka (polecam Lekcję 5 mojego Kursu).

    9. Krystian Karczyński

      Co do pierwszej całki, to ja bym spróbował podstawieniami Eulera.

      Nie ma ich w Kursie, ale opisałem je na blogu tutaj: Podstawienia Eulera III rodzaju

      Robię krok po kroku, tak jak opisałem w powyższym poście:

      -{{x}^{2}}-xrozkładam na czynniki: -{{x}^{2}}-x=x\left( -x-1 \right)

      Moje pierwiastki trójmianu to: {{x}_{1}}=0,\quad {{x}_{2}}=-1

      Stosuję więc odpowiednie podstawienie:

      \sqrt{-{{x}^{2}}-x}=tx

      -{{x}^{2}}-x={{t}^{2}}{{x}^{2}}

      x\left( -x-1 \right)={{t}^{2}}{{x}^{2}}\quad /:x

      -x-1={{t}^{2}}x

      {{t}^{2}}x+x=-1

      x\left( {{t}^{2}}+1 \right)=-1

      x=\frac{-1}{{{t}^{2}}+1}

      Teraz liczę \sqrt{-{{x}^{2}}-x}korzystając z pierwszego podstawienia \sqrt{-{{x}^{2}}-x}=tx:

      \sqrt{-{{x}^{2}}-x}=t\left( \frac{-1}{{{t}^{2}}+1} \right)

      \sqrt{-{{x}^{2}}-x}=\frac{-t}{{{t}^{2}}+1}

      Teraz liczę dxwychodząc od x=\frac{-1}{{{t}^{2}}+1}:

      dx=\frac{2t}{{{\left( {{t}^{2}}+1 \right)}^{2}}}dt

      Wstawiam moje wyliczone x,\quad \sqrt{-{{x}^{2}}-x},\quad dxdo całki \int{\left( 4+x \right)\sqrt{-{{x}^{2}}-x}}dxi mam:

      \int{\left( 4+\frac{-1}{{{t}^{2}}+1} \right)\frac{-t}{{{t}^{2}}+1}}\frac{2t}{{{\left( {{t}^{2}}+1 \right)}^{2}}}dt=-2\int{\left( 4-\frac{1}{{{t}^{2}}+1} \right)\frac{{{t}^{2}}}{\left( {{t}^{2}}+3 \right)}dt}

      Jeszcze tylko mały szczegół: policzyć do końca tą całkę (trzeba ją chyba będzie rozbić na dwie wymierne…) 🙂

  17. Krystian

    Witam.
    Słyszałem o reklamie żebyś był Pan bardziej rozpoznawalny. Otóż Panie Krystianie mój imienniku walisz do mniejszej rzeszy ludzi tzn studentów. Z takim talentem powinien Pan zrobić kursy dla licealistów. Napisać tylko ze to kurs do matury i zarobiłbyś się Pan na Amen. Licealiści głupi naród jak kasę mają to trwonią. Są jeszcze technika ale tam to są \inteligentne lenie i nie ma co liczyć kupno twoich kursów. Przykład: Mam u siebie w klasie rzeszę techników i większość z nich ma twoje kursy ale co z tego skoro nawet nie chce im się ich oglądać. Pomyśl coś Panie Krystianie bo szkoda twojego talentu. Nie spotkałem się z osobą a znam ich sporo która po twoim kursie byłaby niezadowolona. Ostatnio było koło z analizy i ci co oglądali twoje kursy i to powierzchownie dostali 15-17 pkt na 20. Już po 5 lekcjach można było zdać te koło i mieć spokój. Jak byś zrobił takie kursy dla licealistów w końcu przyczyniłbyś się do wzrostu kandydatów na polibudy. Czekam na twoje zdanie: Dzień dobry. Dzięki za pomysł, pomyślimy – zobaczymy.

    Reply

    1. Krystian Karczyński

      Dzięki za radę.

      Parę razy myślałem o zrobieniu Kursów dla szkół średnich. Problem w tym, że ja naprawdę wolę studentów i matematykę na studiach 🙂

    2. Morcin

      lekcje etrapez powinny być sprzedawane w empiku 😀 a co do kursów maturalnych to szkoda że nie ma bo zdawalność matur z mat. by poszła w górę 😉

  18. Mateusz

    Dzień dobry. Wpadłem na ciekawy (chyba) pomysł zareklamowania kursów na jeszcze szerszą skalę. Co powiedziałby Pan na koszulki e-trapez z logiem firmowym? Oczywiście nie zajmuję się tym, rzuciłem tylko taką propozycję. Koszulki można byłoby albo kupować, mogłyby być wysyłane wraz z kursami, ze zniżką dla stałych bywalców. Noszone przez Nas koszulki głównie na uczelniach, akademikach zrobiłyby na prawdę niezłą reklamę. Co Pan o tym sądzi? Pozdrawiam

    Reply

  19. Michał

    Kiedyś, gdy będę już za stary by się uczyć , zasiądę przy kominku , zapalę fajkę i opowiem wnukom o Kursie E-trapez i panu Krystianie ! To Lśniący Diament , któremu za wszystko dziękuję , ponieważ dzięki tym kursom przebiłem się przez 2 semestry trudnej matematyki na Politechnice Warszawskiej . 😀 Wesołych Wielkanocnych

    Reply

  20. Sebastian

    Jeżeli uda się zaliczyć matematykę to tylko dzięki kursom:) Coś czuję, że jak nawiedziłby Pan Kraków dostałby Pan zaproszenie na co najmniej kilka imprez xD. Wesołych Świąt!

    Reply

    3. Krystian Karczyński

      \int{{{a}^{x}}dx}=\int{{{e}^{xln a}}dx}=\left| \begin{matrix}
      & t=xln a \\
      & dt=ln adx \\
      & \frac{dt}{ln a}=dx \end{matrix} \right|=\int{{{e}^{t}}\frac{dt}{ln a}}=\frac{1}{ln a}\int{{{e}^{t}}dt}=\frac{1}{ln a}{{e}^{t}}+C=\frac{1}{ln a}{{e}^{xln a}}+C=\frac{1}{ln a}{{a}^{x}}+C=\frac{{{a}^{x}}}{ln a}+C

  23. Radek

    Odwalasz kawał pięknej roboty, przyjacielu 🙂 Bez Twoich wyjaśnień matematyka to, czarny, gęsty las, pełen niebezpiecznej, drapieżnej zwierzyny… A po obejrzeniu Twojego filmu – matma staje się łąką pełną kwiatów oblaną słońcem 🙂
    Dzięki!

    Reply

    2. Gabriela

      Zgadzam się całkowicie! 

      Bardzo dziękuje za pomoc w przetrwaniu na studiach

      Uratował Pan wiele, wiele dusz…

Leave a Reply

Twój adres e-mail nie zostanie opublikowany. Wymagane pola są oznaczone *

Twój komentarz będzie dostępny publicznie na naszej stronie razem z powyższym podpisem. Komentarz możesz zmienić, lub usunąć w każdej chwili. Administratorem danych osobowych podanych w tym formularzu jest eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. Zasady przetwarzania danych oraz Twoje uprawnienia z tym związane opisane są w Polityce Prywatności.