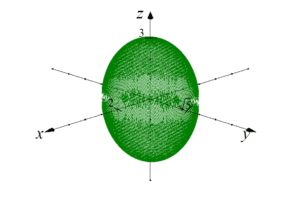Powiedzmy, że do policzenia mamy objętość elipsoidy:
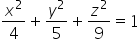
Jest to elipsoida, która przecina osie x,y,z we współrzędnych odpowiednio: 2,
i 3 (równanie ogólne elipsoidy to: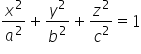 
, gdzie a,b, c to współrzędne przecięcia).
Nie jest to elipsoida obrotowa, nie powstaje przez obrót jakiejkolwiek krzywej wokół jakiejkolwiek osi, nie poradzimy sobie standardowym wzorem na objętość bryły obrotowej:
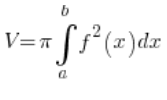
Trzeba kombinować inaczej.
1. Obieramy dowolny punkt M(z) w środku elipsoidy i na osi OZ.
Płaszczyzna przechodząca przez ten punkt i prostopadła do osi OZ „wycina” nam z elipsoidy pewną elipsę:
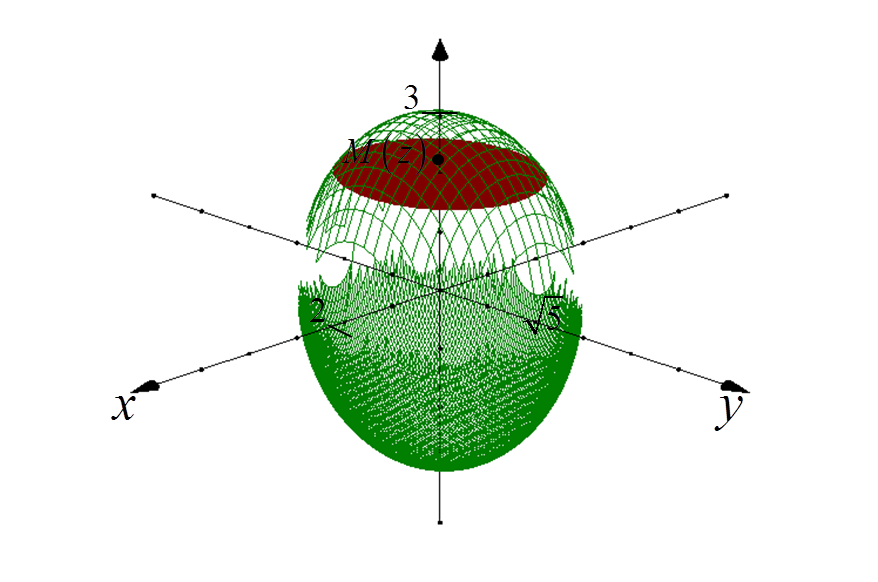
2. Wyznaczamy równanie rzutu „wykrojonej” elipsy na płaszczyznę XY
Równanie tej elipsy, dla ustalonego ‚z’ (traktujemy ‚z’ jak stałą) wyznaczamy z równania ogólnego elipsoidy:
/:
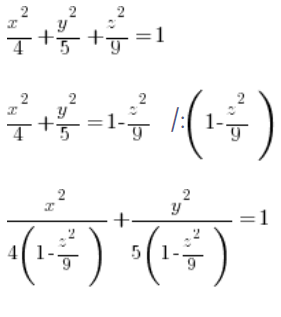
Widać, że nasze ‚a’ i ‚b’ z równania ogólnego elipsoidy (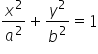
), to:
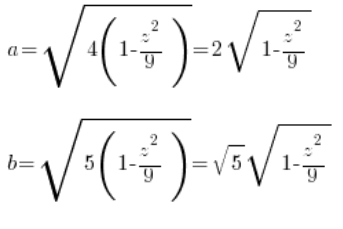
4. Obliczamy pole tego przekroju w zależności od zmiennej ‚z’
Pole tej elipsy wyjdzie zależne od obranego punktu ‚z’, czyli będzie to jakby funkcja zmiennej ‚z’. Obliczymy je albo z gotowego wzoru na pole elipsy (
):
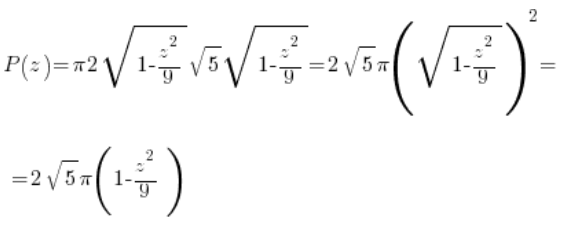
Albo licząc pracowicie odpowiednią całkę oznaczoną (wykorzystując oczywiście postać parametryczną elipsy i wzór na pole obszaru w postaci parametrycznej):
(liczymy, liczymy, liczymy…)=
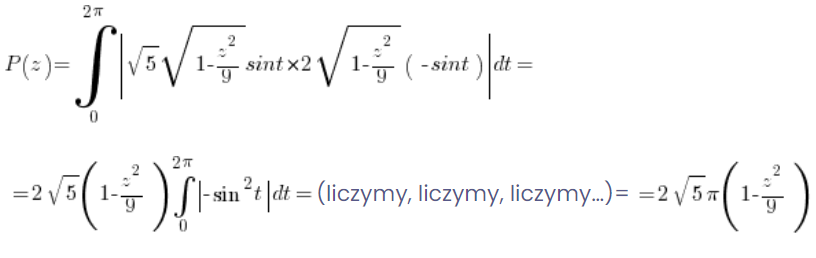
5. Liczymy objętość bryły przy pomocy pól przekrojów
Teraz trudny moment. Objętość bryły równa jest – to trochę nieładnie zabrzmi – „sumie” (czyli całce) wszystkich przekrojów, czyli ogólnie:
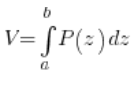
gdzie 
to funkcja pól przekrojów bryły płaszczyzną prostopadłą do osi OZ, a ‚a’ i ‚b’ to granice, w których zmienia się ‚z’.
Czyli u nas:
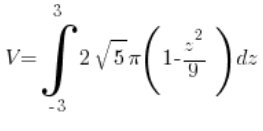=(liczymy, liczymy, liczymy…)=
Co się zgadza z ogólnym wzorem na elipsoidę (
).
KONIEC
Warto zapamiętać ten ogólny schemat i przede wszystkim to, że objętość trudniejszych, nie-obrotowych brył można policzyć całkując funkcję ich pól przekrojów.
Monika napisał
Witam, nie mogę sobie poradzić z pewnym poleceniem. Proszę o pomoc gdyż niedługo mam egzamin z analizy a chcę to dobrze zrozumieć. Polecenie brzmi : Oblicz objętość brył ograniczonej powierzchniami x^2+y^2=hz,z=h. Jak się do tego zabrać bardzo mi na tym zależy.
To będzie paraboloida ograniczona z góry płaszczyzną. Zacząć trzeba oczywiście od rysunku.
Równanie jej rzutu na płaszczyznę XoY to będzie:
, czyli swojskie kółeczko o promieniu h.
Dalej wszystko ładnie się składa (trzeba przejść na współrzędne biegunowe).
Monika napisał
Niestety ale gubie sie w obliczeniach jestem przyzwyczajona ze promien przyjmuje wartosci liczbowe i cos mi sie nie zgadza. Czy da Pan rade to rozwiązać z komentarzami co i jak się robi?
Piotrek napisał
Witam,
mam za zadanie wyznaczyć wierzchołek paraboloidy. Uważam, że dwie elipsy jednoznacznie wyznaczą mi kształt paraboloidy. Środki ciężkości obu elips leżą na jednej prostej (nie w tych samych płaszczyznach).
Bardzo prosiłbym o pomysły rozwiązania takiego zagadnienia.
Piotrek napisał
Wyznaczą kształt elipsoidy a nie paraboloidy. Należy dodać, że środek elipsoidy nie znajduje się pomiędzy elipsami. dane to wymiary elips oraz odległość miedzy nimi.
Nie jestem dobry z geometrii wykreślnej, przykro mi…