Współrzędne eliptyczne (całki podwójne)

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Bywają w życiu takie sytuacje, kiedy obszarem całkowania w całce podwójnej jest elipsa….

Co wtedy?

Współrzędne eliptyczne

Zgrabną metodą rozwiązania jest najczęściej zastosowanie tzw. współrzędnych eliptycznych. To coś takiego jak współrzędne biegunowe, mechanizm działania jest zupełnie podobny, tylko co innego podstawiasz za x i za y i inny jest jakobian. Interpretacja ‘r’ także jest inna. No podsumowując, jeśli umiesz przechodzić na współrzędne biegunowe (a robi się to najczęściej kiedy obszarem całkowania jest koło) to bez trudu załapiesz też eliptyczne.

Mamy więc całkę: 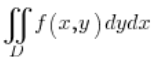i obszar całkowania ograniczony elipsą o środku w początku układu współrzędnych, której równanie jest: 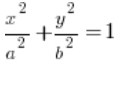. Niech tam po prawej stronie równania elipsy będzie na pewno 1-ka, dobra? Jakby była na przykład 9 możesz ją łatwo zrobić, dzieląc obie strony równania przez 9.

Obszar całkowania narysowany wygląda tak:

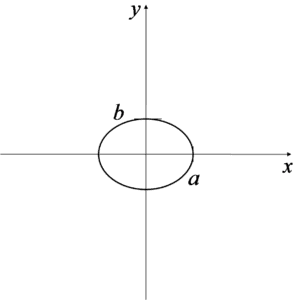
Co oznaczają a i b każdy widzi na rysunku. Trzeba uważać, bo jak w równaniu elipsy jest w mianowniku pod na przykład 9, to znaczy, że , wiadomo dlaczego, prawda?

No i teraz mając taką “czystą” sytuację przechodzimy na współrzędne eliptyczne, podstawiając:

Znaczenie zmiennych we współrzędnych eliptycznych

Kąt oznacza dokładnie to samo co we współrzędnych biegunowych, a dla odmiany co innego. W zadaniach podstawowych z elipsą daną ładnym równaniem 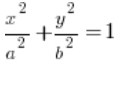przyjmuj po prostu, że zmienia się od zera do jeden (w bardziej skomplikowanych wstaw i do równania elipsy i wylicz górne ograniczenie r).

Jakobian

Jakobian we współrzędnych eliptycznych równy jest

Pamiętając o jakobianie przechodzimy więc na całkę we współrzędnych eliptycznych:

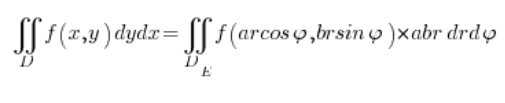
gdzie zmienne i są ograniczone: w granicach od zera do jeden, a w zależności czy mówimy o całej elipsie, czy o połowie, czy o np. ćwiartce różnymi wartościami kąta – tak jak we współrzędnych biegunowych.

Tylko brać i liczyć.

Przykład

Oblicz całkę 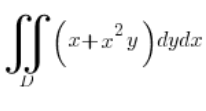, gdzie D jest elipsą o równaniu: .

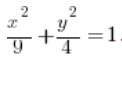Zgodnie z powyższym schematem podstawiamy:

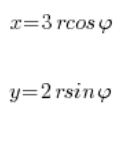
Bierzemy obszar całkowania:

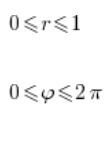
I liczymy całeczkę:

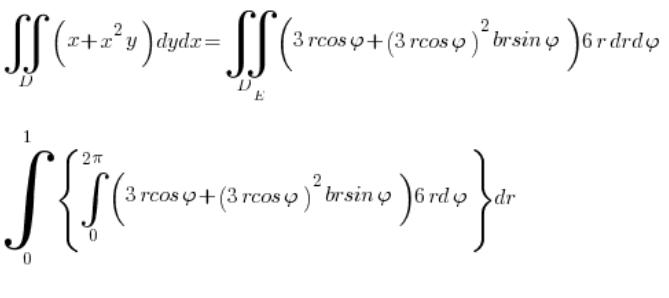
Co już jest oczywiście formalnością 🙂

Co słychać ogólnie?

Co do spraw ogólnych, w tej chwili pracuję nad Kursem Całek Wielokrotnych, a w marcu będę pokazywał na blogu trochę fajnych narzędzi ułatwiających mocno pracę nad tymi całkami. Będą to na przykład bajerancki kalkulator online do całek podwójnych i fajny program do dwu i trzy wymiarowych wykresów funkcji.

Zachęcam więc do zaglądania na bloga i zapisywania na newsletter, pozdrawiam i sukcesów w bojach z całkami podwójnymi!