Całki oznaczone przez podstawienie – zmiana granic całkowania
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
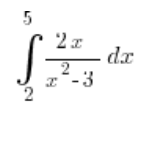
Powyższą całkę oznaczoną należy rozwiązać przez podstawienie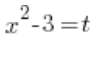 
i tu się wszyscy zgadzamy. Co jednak z granicami całkowania?
Granice całkowania w całkowaniu przez podstawienie w całce oznaczonej
Czy można zapisać:
?
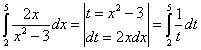Oczywiście nie. Problem z granicami całkowania. W całce oznaczonej po lewej dotyczą się one zmiennej 
, a po prawej zmiennej 
, powinny więc także ulec zmianie razem ze zmienną.
Jednym wyjściem (zalecam je w swoim Kursie) jest kompletne ominięcie problemu, poprzez rozwiązanie całki nieoznaczonej (bez granic całkowania) na boczku i później wstawienie do wyniku (ze zmienną x) granic całkowania 5 i 2.
Drugim wyjściem jest stawienie czoła problemowi w otwartej walce i zamiana granic całkowania zgodnie z podstawieniem. Skoro granice w zmiennej x wynoszą: 2 i 5, po podstawieniu: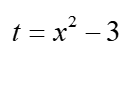 
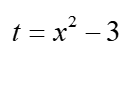
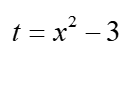
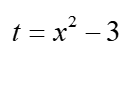
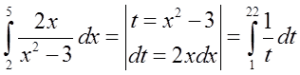
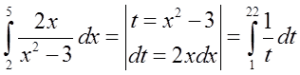
wyniosą one w zmiennej t odpowiednio: 1 i 22, a wyniki te uzyskałem podstawiając 2 i 5 za x-sa do podstawienia . Prawidłowym przejściem więc było by:
Jedna z wielu opinii o naszych Kursach...
Śmieszne pieniądze za porządny kurs, a wielu wykładowców tłumaczy bez pasji i nawet na konsultacjach im się nie chce dodatkowo tłumaczyć, a tutaj mogę kilka razy tego samego słuchać jak potrzebuje.Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Mam pewne pytanie:
Otóż mamy sobie całkę w granicach od 0 do 2. Po podstawieniu za t , następuje zmiana granic, za 0 ->0 a za 2 -> -2. Moje pytanie: czy całka będzie w granicach analogicznie do pierwotnej całki, od 0 do -2, czy natomiast w granicach od -2 do 0, od najmniejszej do największej.
Wiem być może jest to błahe pytanie ale mnie ono trapi.
Z góry dziękuje za odpowiedz.
a kiedy podstawiamy ‘t’ za ‘ln x’?
Na przykład w takiej całce:
\int{\frac{ln x}{x}dx}
Albo w takiej:
\int{\frac{{{ln }^{2}}x}{x}dx}
Albo w takiej:
\int{\frac{dx}{xln x}}
Może być i w tej:
\int{\frac{{{cos }^{2}}\left( ln x \right)}{x}dx}
Niestety, jak widać nie jest możliwe sformułowanie jakiejś bardziej ogólnej odpowiedzi na pytanie “kiedy bierzemy za t lnx”.
W ogóle w całkach przez podstawienie niestety nie ma reguł typu: “jak jest ułamek, to bierzemy licznik”, albo “jak jest COŚ to podstawiamy COŚ”. Jedyna droga, żeby się tego nauczyć to żmudna metoda prób i błędów…
Przepraszam, za źle sformułowane, niepełne pytanie. Miałem na myśli, jak zmienią się granice całkowania, jeśli za ln x podstawimy t? 🙂
Przykład jak najbardziej trafny, nie ważne czy w liczniku jest pochodna mianownika i czy tą całkę da się łatwiej policzyć , ważne jest to by zrozumieć w jaki sposób zmieniamy granice całkowania. Więc darujcie sobie komentarze o złym przykładzie. Ja uważam , że blog jest poprowadzony bardzo dobrze a jeszcze bardziej polecam kursy do odsłuchania;) inwestycja mi się zwróciła;)
słaby przykład, w liczniku pochodna mianownika hehe
Poprawiłem pomyłkę, sorry!
u nas Mrozu na PG co chwile się mota w prostych rachunkach, ale potrafi czasem niezłe combosy wycyrać
2^2-3 = 4?
5^2-3 = 25?
Takie błędy i “zalecam je w swoim Kursie”…
Naucz się rachować