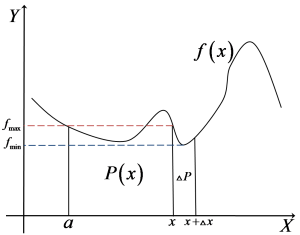Całki Nieoznaczone Wykład 2
Temat: Całki nieoznaczone i pola obszarów.
Streszczenie
Na wykładzie pokażę dziwną – zdawało by się – rzecz. Okaże się, że funkcję pierwotną z funkcji 
można interpretować geometrycznie jako pewną funkcję pola związanego z tą funkcją – czyli rzecz pozornie zupełnie nie związaną z tymi prędkościami i saneczkami, które rysowałem na poprzednim wykładzie.
Co już trzeba umieć?
Przed przystąpieniem do czytania powinieneś już wiedzieć, co to jest całka nieoznaczona i funkcja pierwotna (poprzedni Wykład).
Video
Na tym filmiku pokazuję najważniejsze rzeczy z Wykładu, zapraszam:
Zaczynamy. O jaką funkcję i o jakie pole chodzi?
Całka nieoznaczona to rodzina funkcji pierwotnych do pewnej funkcji . Pierwotnych, tzn. takich, których pochodna daje . Narysujmy sobie tą naszą :
Czy ta funkcja, to już właśnie nasza funkcja pierwotna? No oczywiście nie – pierwotna funkcja to taka, której pochodna da tą narysowaną .
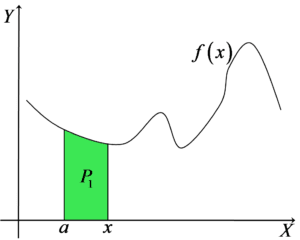
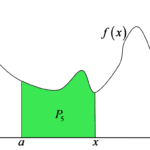
Zamieszajmy trochę na tym rysunku i zaznaczmy następujące pole obszaru:
Jest to pole, które może nie tak łatwo policzyć (bo nie jest to jakaś podstawowa figura geometryczna), ale które na pewno ma jakąś określoną wartość, np. 10, albo 
. W tym momencie nie zajmujemy się tym, jaką.
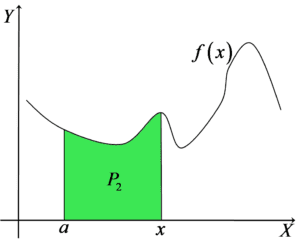
Przyjmując, że 
jest stałą i przesuwając 
otrzymamy jakieś inne pole:
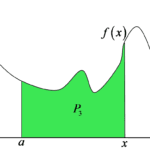
No i jasnym jest, że przesuwając sobie ten (umawiamy się, że jest granicą, tzn. 
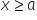) otrzymamy różne wartości pola pod funkcją :
Wartości pól zmienią się w zależności od , możemy więc powiedzieć, że wszystkie skonstruowane jak wyżej pola są wartościami pewnej FUNKCJI POLA zależnej od x. Oznaczamy ją jako:
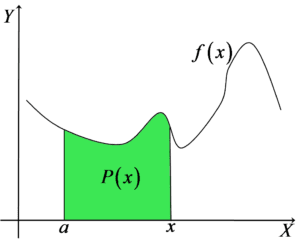
Ogólnie na rysunku zaznaczyć to można tak:
Rozumiemy, że dla różnych argumentów funkcji x otrzymamy różne wartości pola .
Mamy więc dwie funkcje:
i
Jaki jest związek pomiędzy nimi?
Proszę Państwa, ni mniej ni więcej taki, że jedna jest funkcją pierwotną drugiej – albo innymi słowy, że druga jest pochodną pierwszej (z poprzedniego Wykładu wiemy, że pochodna i funkcja pierwotna to pojęcia jakby “odwrotne”).
Wykażemy to dalej.
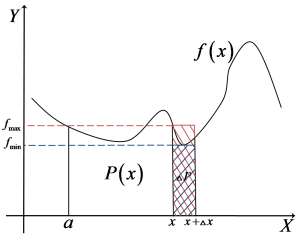
Funkcja pola P(x) to funkcja pierwotna funkcji f(x) – wykazujemy
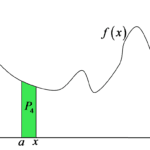
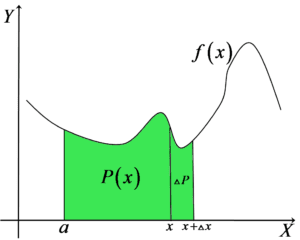
Wróćmy do naszego wykresu i wyobraźmy sobie, że przesuwamy x nie o 1, ani o 10, ani o 
jednostek w prawo tylko o pewną nieokreśloną (na razie) wartość 
:
Po takim przyroście nasze pole również wzrośnie o 
.
Zaznaczmy teraz najmniejszą i największą wartość funkcji w przedziale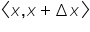 
jako 
i 
:
Każda z nich wyznacza nam pewien prostokąt (odpowiednio niebieski i czerwony):
Są to prostokąty o boku, którym jest odcinek o długości i drugim boku którym jest lub . Oczywistym jest (spójrz na rysunek i zastanów się, czy w ogóle mogło by być inaczej), że nasze pole jest większe pola niebieskiego prostokąta i mniejsze od pola czerwonego prostokąta, czyli:
Dzieląc te nierówności obustronnie przez otrzymamy:
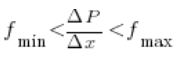
Teraz ważny moment:
Jeżeli nasze będzie dążyło do 
, czyli będzie nieskończenie małe, to wartości i będą dążyły do , czyli wartości funkcji w punkcie x. Prześledź to sobie na ostatnim wykresie i wyobraź, że przyrost jest coraz mniejszy i mniejszy i mniejszy… Jak zachowywać się będą i ? Będą coraz bardziej przybliżać się do (właściwie na naszym konkretnym rysunku już teraz 
).
Jeśli więc w nierówności:
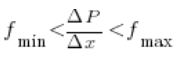
…przy 
zachodzi coś takiego, że:
i 
, oczywistym jest, że 
(a mówi o tym na przykład twierdzenie o trzech funkcjach).
Mamy zatem – zapisując powyższe symbolicznie:
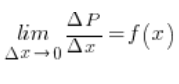
A czym jest wyrażenie po lewej stronie równości? Stosunek przyrostu wartości funkcji i przyrostu argumentu dla nieskończenie małego przyrostu argumentu? Jak pamiętamy z Wykładów o pochodnej jest to DOKŁADNIE pochodna z tej funkcji.
Wykazaliśmy więc, że:
…czyli że pochodna z funkcji pola równa jest funkcji , albo (to jedno i to samo), że:
FUNKCJA POLA JEST FUNKCJĄ PIERWOTNĄ FUNKCJI
Wzór na pole
Mamy więc funkcję i funkcję do niej pierwotną . Całka nieoznaczona była rodziną wszystkich funkcji pierwotnych funkcji. Funkcja jest więc jedną z tych funkcji. Czym odróżnia się od innych? Z poprzedniego Wykładu wiemy, że funkcje pierwotne różnią się o STAŁĄ. Zatem jeśli weźmiemy za 
jakąkolwiek inną funkcję pierwotną do , otrzymamy:
Jeżeli w powyższym równaniu przyjmiemy sobie 
, wyznaczymy stałą C, czyli wartość, o którą różni się od dowolnie innej funkcji pierwotnej:
(spójrz na nasz wykres i zobacz, co będzie, gdy przyjmiemy w nim ), czyli:
Wracając więc z wyznaczoną stałą C do wzoru otrzymamy:
Mamy więc potężny wzór na pole. Możemy je liczyć… całkując (znajdując funkcje pierwotną i wstawiając do niej za i odpowiednie wartości). Potężny, bo nie jesteśmy już ograniczeni do liczenia pól okręgów, trójkątów, trapezów (czyli takich, do których mamy |wzorki”). Możemy spokojnie liczyć powierzchnię obszarów nieregularnych – jezior, lasów, czy co nam tylko do głowy przyjdzie.
Przykład
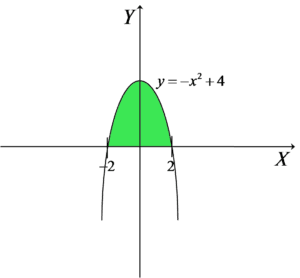
Oblicz pole pomiędzy osią OX a wykresem funkcji 
.
Na wykresie te pole wyglądało by tak:
Z tym – przecież bardzo prostym zadaniu – zostalibyśmy całkowicie bezradni znając tylko wzory na trapez, równoległobok, koło itd. ze szkoły średniej. No może nie całkowicie, bo moglibyśmy sobie policzyć to “w przybliżeniu” (dzieląc np. pole pod parabolą na małe prostokąciki). Ale od dzisiaj (a właściwie od gdzieś tak XVII wieku) mamy dodatkową artylerię.
Posłużymy się więc naszym wzorem na funkcję pola:
Za nasze przyjmujemy “początek” pola na osi OX, czyli 
. Za x przyjmujemy “koniec” pola na osi OX, czyli: 
. Funkcją pierwotną (obliczaną przez całkowanie) do funkcji 
jest funkcja 
(prosta całka). Mamy więc:
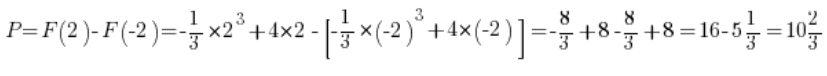
Czyli pole pod parabolką równe jest ni mniej ni więcej tyle. Możemy szykować odpowiednią ilość cementu do zalania, albo trawy do zasiania albo czegokolwiek, co było nam potrzebne 🙂
KONIEC
Pisząc tego posta korzystałem z…
1. “Rachunek różniczkowy i całkowy. Tom II.” G.M. Fichtenholz. Wyd. 1966.
Kliknij tutaj, aby przypomnieć sobie, czym jest całka nieoznaczona (poprzedni Wykład) <–
Kliknij tutaj, aby powrócić na stronę z wykładami o całkach nieoznaczonych