الاقتصاد القياسي – المحاضرة 1
الموضوع: ما هو الاقتصاد القياسي؟
سألني الكثير من الأشخاص:
الاقتصاد القياسي – ما الذي يعنيه هذا المصطلح؟
خصوصًا عندما يسمعون أنني أدرس “علوم الحاسوب والاقتصاد القياسي” (نعم، نعم، على غير المتوقع هناك مثل هذا التخصص الجامعي). الاسم مثير للفضول، هذا صحيح. لكن كما يتضح فإن جوهر الاقتصاد القياسي بحد ذاته ممتع. يمكن القول حتى إنه “عملي” – أي أن ما نتعلمه يمكننا استخدامه في الحياة الحقيقية 🙂
ما الذي تحتاجه لتبدأ رحلتك مع الاقتصاد القياسي؟
آلة حاسبة لإجراء الحسابات البسيطة، بعض المعلومات الأساسية عن الدوال المختلفة، قليل من الخيال، والقدرة على ربط الحقائق. البقية ستأتي وحدها.
لنبدأ بمثال قصير.
المثال 1
في مجموعة من الطلاب تم اختيارهم عشوائيًا، سُئلوا: كم من الوقت خصصوا للدراسة قبل اختبار مهم (بالساعات). بعد ذلك، تم التحقق من الدرجة التي حصلوا عليها. في الجدول سُجّلت النتائج:
هممم… النظر إلى الأرقام المجردة قد لا يخبرنا بالكثير. لذلك من المفيد رسم مخطط منفصل لكل متغيّر، أي تحديد درجة الطالب ووقت دراسته.
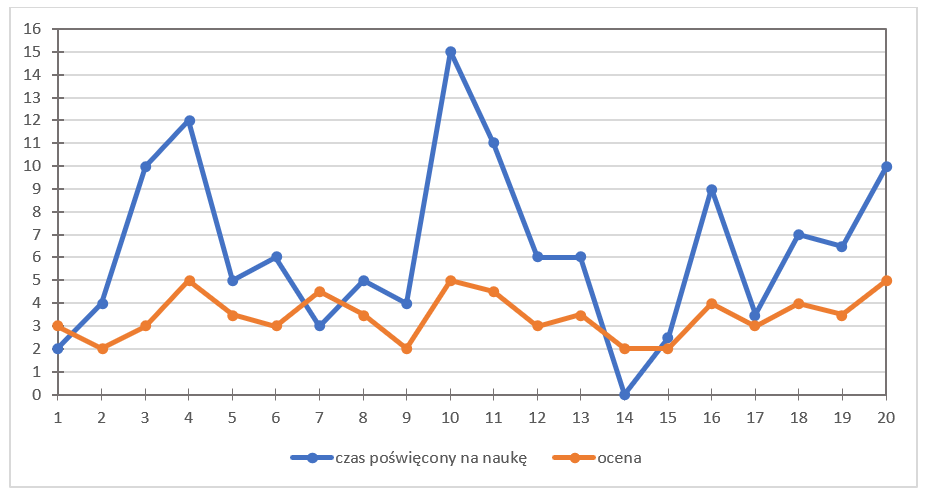
ها هو المخطط:
من أين أتت هذه “الموجات”؟ المحور الأفقي OX يمثل رقم الطالب، بينما المحور العمودي OY يعكس قيمة الدرجة (المخطط البرتقالي)، وكذلك عدد ساعات الدراسة (المخطط الأزرق). تحديد أزواج النقاط أمر مهم جدًا، لذا خذ وقتك لتتأمل الجدول والنقاط المحددة.
وضعتُ هذين المخططين في رسم واحد عن قصد. لماذا؟ لنتمكن من النظر وتحليل كيف تتصرف المتغيرات ليس بالنسبة لكل طالب على حدة، بل بشكل عام بالنسبة لبعضها البعض. ربما هناك علاقة بين وقت الدراسة والدرجة في الاختبار؟
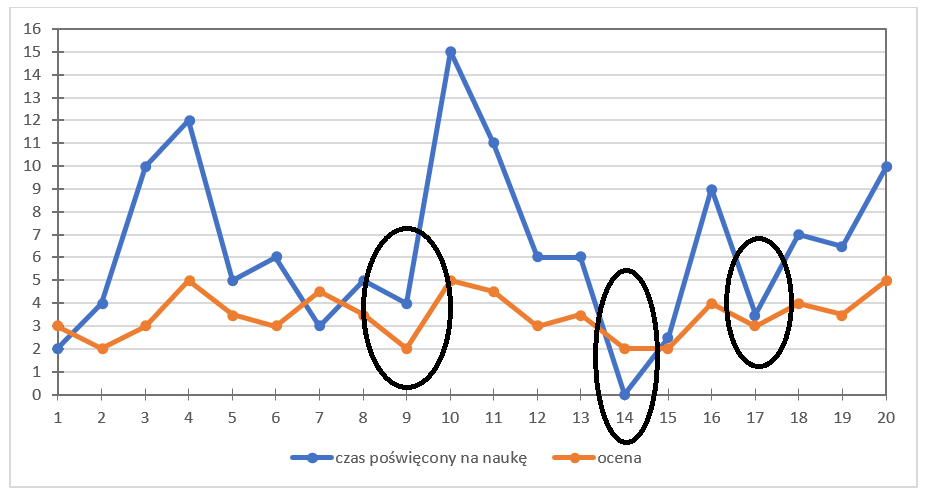
بالتأكيد ترى أن هذه المخططات تحتوي على “قمم” و”قيعان”. هل تتطابق هذه القمم والقيعان عند نفس الطالب؟
بالطبع، معك حق – نرى ذلك بوضوح. على سبيل المثال، هناك قمم: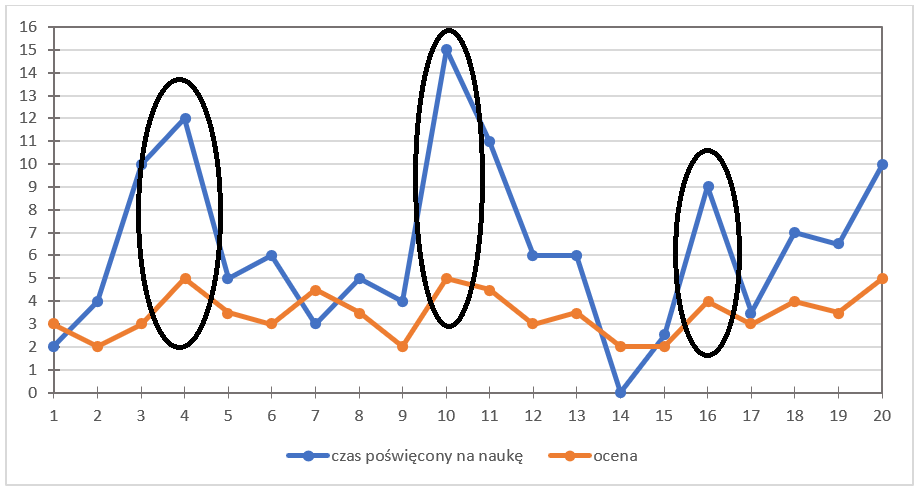
وهنا قيعان:
كما ترى، من خلال تحليل بيانات تعكس ظاهرة معينة (حسنًا، بالنسبة لبعض الأشخاص، الدراسة قبل الاختبار قد تُعتبر “ظاهرة” 🙂 ) يمكنك ملاحظة بعض العلاقات. ما رأيك بها؟
تمامًا، يتضح (خصوصًا من خلال المخطط) أنه كلما درست أكثر، كانت درجتك أعلى وأفضل (والعكس صحيح). عادةً ما يكون هذا صحيحًا. بل صحيح جدًا. لكن يجدر تذكّر أن لكل قاعدة استثناءات. (تذكرت الآن مقولة طريفة: تعرف لتحصل على 2، تحسب لتحصل على 3، تنال 4، وتتساءل لماذا ليست 5 🙂).
حسنًا، بما أننا وصلنا إلى استنتاج أن هناك علاقة بين هاتين الصفتين، فلنحاول رسم مخطط جديد لهذه البيانات – هذه المرة بجعل وقت الدراسة يعتمد على الدرجة. أي أن الأزواج من النقاط التي سنضعها في نظام الإحداثيات لن تكون رقم الطالب والصفة، بل فقط الصفتين معًا، أي:
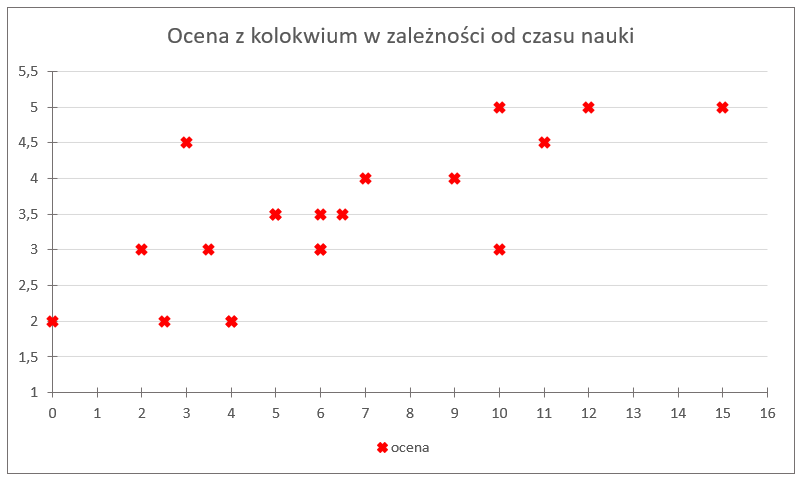
لنقل إن وقت الدراسة سيكون متغيرنا X، أما الدرجة التي حصل عليها الطالب فهي المتغير Y. ومن هنا نحصل على النقاط المرسومة:
هنا كما نرى من الصعب جدًا توصيل كل النقاط بخط مكسور واحد. هذا غير ممكن. لكن هذه “السحابة” من النقاط تصطف بطريقة مميزة، انظر:
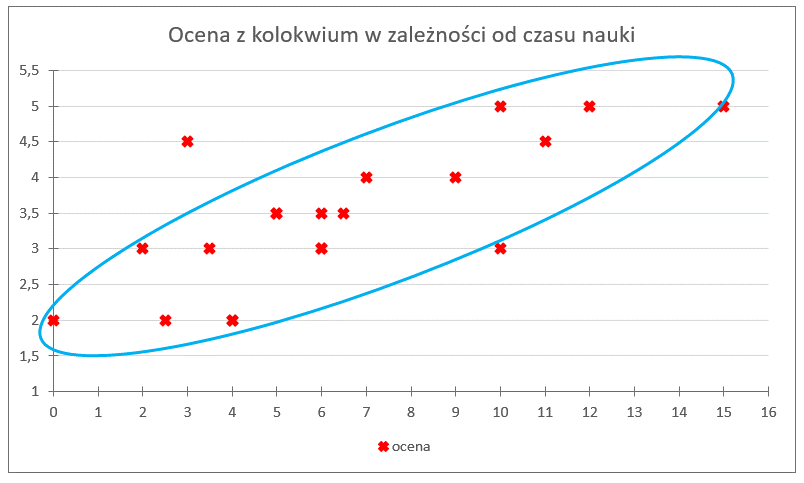
ما رأيك بهذا الشكل؟ بالميل؟
كما نرى، فإنها تصطف “بشكل جميل” وممتد، مائلة نحو الأعلى. أي أن العلاقة التي لاحظناها (كلما زاد وقت الدراسة، ارتفعت الدرجة) تم تأكيدها. أما بالنسبة للشكل، يمكن أن نخطو خطوة للأمام ونقول إنه ذو طابع خطي، أي قريب من خط مستقيم صاعد يغطي معظم هذه السحابة من النقاط.
تبين أن العلاقة القائمة بين هاتين الصفتين يمكن التعبير عنها رياضيًا. رائع!
بالطبع يجب أن نتذكر دائمًا أن هذا ليس الوصف الدقيق لهذا الترابط، بل هو دالة تقريبية تحاول أن تشرح العلاقة بأفضل شكل ممكن. وهنا لدينا شيء مشابه لخط مستقيم، أي دالة خطية.
وبما أننا أثبتنا أن معظم النقاط يمكن تقريبها بدالة واحدة، فيمكن القول إنه يمكننا قياسها. يبقى فقط أن نحدد كيف نُنشئ هذه الدالة ونحسبها، وما الفائدة منها؟
هنا يأتي دور الاقتصاد القياسي!
مفهوم الاقتصاد القياسي
قبل فترة ليست طويلة، في بداية القرن العشرين، كان هناك بولندي جمع كلمتين يونانيتين: oikonomia (وتعني: الإدارة أو الاقتصاد) وmetron (وتعني: المقياس) فأنشأ كلمة جديدة – الاقتصاد القياسي. وبالمعنى الحرفي هو “قياس الاقتصاد”.
يبدو منطقيًا 🙂 لأن هذا بالضبط ما يقوم به الاقتصاد القياسي – قياس القوانين والأنماط الموجودة في الظواهر الاقتصادية باستخدام بعض الطرق الرياضية والإحصائية. فهو يشرح سلوك متغير معين اعتمادًا على سلوك متغيرات أخرى.
أي أن الرياضيات ليست وحدها المهمة هنا، بل أيضًا الإحصاء. فلا ينبغي أن تكون البيانات مأخوذة عشوائيًا من الخيال، بل يجب أن تكون واقعية. البيانات التي جُمعت وسُجلت تُسمى بيانات إحصائية. لذلك يمكن اعتبار الاقتصاد القياسي “ابنًا طبيعيًا” لعلم الإحصاء.
بالعودة إلى المثال: لاحظنا علاقة بين متغيرات ملموسة و”واقعية”، لذا يمكن القول أيضًا إنها علاقة بين متغيرات اقتصادية.
افترض الآن أن الطالب رقم 21، استنادًا إلى تحليل بيانات زملائه، يريد أن “يحسب” تقريبًا كم من الوقت عليه أن يدرس ليحصل على درجة معينة (لنقل إنه يرضى بدرجة 3 أو 3.5). أو – إذا درس نصف يوم – فما الدرجة التي يمكن أن يتوقعها؟
للإجابة على هذه الأسئلة، أي لنتمكن من “الحساب”، نحتاج إلى معادلة محددة. وهنا يظهر مفهوم آخر – النموذج الاقتصادي القياسي.
مفهوم النموذج الاقتصادي القياسي
الأداة الأساسية المستخدمة في التحليل الاقتصادي القياسي هي النموذج الاقتصادي القياسي. النموذج (لا، ليس نسخة ذكورية من “العارضة” 🙂 ) هو بناء نظري رسمي يُحلل بدلاً من الظاهرة الواقعية. يسمح بفهم أفضل لطبيعة الظاهرة. من خلال معادلة أو عدة معادلات، يوضح العلاقات بين العناصر التي اخترناها من الصفات الاقتصادية. وبالتالي فهو نموذج رياضي “مكيّف” مع الواقع باستخدام الطرق الإحصائية المناسبة.
ضع في اعتبارك أنه دائمًا ما يكون صورة مبسطة جدًا للظاهرة التي نراقبها. مثل نموذج الطائرة أو نموذج الحلزون المزدوج للـ DNA. فهو يوضح بشكل “تصويري” شيئًا موجودًا في العالم الحقيقي. وسأذكر فورًا أن النموذج الاقتصادي القياسي يأخذ في الاعتبار أهم عناصر وصف الواقع، بينما يتجاهل الأقل أهمية. وأظن أنك توافقني، لأنه من المستحيل أخذ كل الاحتمالات بعين الاعتبار 🙂
التعبير الرسمي للنموذج هو معادلة. هذا شكله الأكثر عمومية:
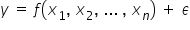
مم يتكون مثل هذا النموذج؟ له عدة عناصر أساسية:
أولًا، المتغير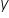 
– وهو المتغير الذي تريد تفسير سلوكه بواسطة النموذج. لذلك يُسمّى «المتغير التابع» أو «المفسَّر».
أما المتغيرات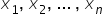 
فهي n من «المتغيرات المستقلة/المفسِّرة». وهي التي سنستخدمها في التفسير. أحيانًا تكفي متغير واحد مفسِّر. وبالطبع لكل منها مضمون اقتصادي محدد.
الدالة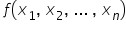 
هي صياغة للعلاقة الدالية بين المتغير التابع والمتغيرات المستقلة وكذلك المكوّن العشوائي.
أما تلك الحرف الغامض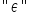 
المشابه لحرف «E» الأنيق فهو إبسيلون (ε)، حرف يوناني يرمز إلى ما يُعرف بـ «المكوّن العشوائي». كلمتان عنه:
يُجسّد المكوّن العشوائي في النموذج «الاضطرابات» الناتجة عن عوامل أخرى. فنحن نتعامل مع المعادلة الرياضية دائمًا كقيمة تقريبية. لذا يأخذ المكوّن العشوائي في الحسبان – من جملة أمور – الفروقات بين النموذج والواقع، وتأثير متغيرات غير مدرجة في النموذج، وأخطاء قياس المتغيرات، وكذلك العوامل العشوائية غير المتوقعة.
أوف… كمٌّ من النظرية!
لِنَعُد إلى مثالنا. ثبت أن بين الصفتين علاقة خطية. وهنا تفيدنا معلوماتنا من المدرسة الإعدادية: كيف كانت صيغة الدالة الخطية؟
كانت هكذا: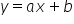 
.
تُجمع المتغيرات وتُضرب بمعاملات (سكاﻻرات) مناسبة تُسمّى «معلمات» (a, b). فهل يكون هذا نموذجنا؟
الإجابة – «تقريبًا نعم» 🙂
المعادلة المكتوبة تمثّل نموذجًا نظريًا. ولتمييزه في الصياغة عن النموذج العام نضع قبعة فوق y. فتكون المعادلة:
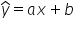
وهذا يمكن اعتباره نموذجًا اقتصاديًا قياسيًا نظريًا.
لم يكن الأمر صعبًا علينا 🙂
كيف يبدو بصيغته العامة التي تراعي كل شيء، بما في ذلك المتغيرات المهملة والأقل أهمية؟ هكذا:
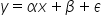
هذا للحالة ذات المتغير الواحد. أما لعدة متغيرات:
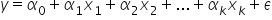
وغالبًا ما تُستخدم في الصيغ الرسمية الحروف اليونانية (ألفا، بيتا، إلخ) لوصف المعلمات، أي ما سنعبر عنه لاحقًا بأعداد.
في مثالنا كنّا نفسّر اعتماد درجة الاختبار على وقت الدراسة. لكن ربما ينبغي أن تكون العلاقة بالعكس، أي يعتمد وقت الدراسة على الدرجة؟ إذًا يمكننا دراسة نموذج كهذا:
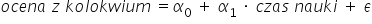
أو نموذجًا كهذا:
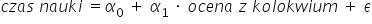
هنا تفيدنا معارفنا العقلانية ومعرفتنا بعلاقات السبب والنتيجة؛ فكما ترى فالنموذج الثاني يفتقر إلى المعنى. إذ كيف سنقيس وقت الدراسة لامتحان ما بينما لدينا بالفعل درجته؟ 🙂
إذًا فالنموذج العام يكون على الصورة: .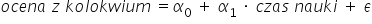
ماذا يختبئ تحت «إبسيلون» هذه؟
متغيرات أخرى لا ندرجها، مثل عدد مرات الحضور للمحاضرة، مزاج المُحاضِر، إلخ. وهناك أيضًا أحداث عشوائية خفية، كإصابة الطالب بمرض مفاجئ – فمع أنه درس كثيرًا، إلا أن الوهن وضعف التركيز أدّيا إلى درجة أدنى.
الآن تتمثّل مهمة الاقتصاد القياسي في حساب القيم المناسبة لـ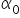 
و
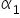. عندها سنحصل على قيم عددية مُقدَّرة تُرمز عادةً بـ 
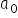و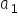
، أو إن شئت فـ 
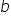و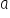
على الترتيب. مثلًا شيء كهذا:
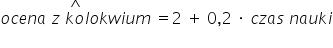
أما كيفية حساب هذه القيم العددية فذلك موضوع آخر 🙂
هناك طرق كثيرة، لكل منها مبررات تطبيقها. في هذا النموذج بالتحديد افترضنا علاقة خطية، وهي الأبسط في التحقق والتطبيق.
بالطبع يمكن أن تكون الدالة 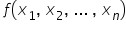التي تصف العلاقات بين المتغيرات المفسِّرة بأي صيغة كانت (أسّية، لوغاريتمية، كسرية، إلخ أو مزيجًا من عدة صيغ). ويبقى علينا الآن التحقق مما إذا كان النموذج جيدًا (أي يحقق الافتراضات المناسبة)، ثم استخلاص بعض النتائج وتطبيقه – مثلًا لحساب القيم المرغوبة للطالب رقم 21.
كما ترى، فموضوع الاقتصاد القياسي ليس مملًا أبدًا. صحيح أن فيه قدرًا من الحسابات – الكثير من الأرقام والصيغ والمخططات (كما هو الحال دائمًا في الإحصاء). لكن إن فكرت جيدًا فيما تريد تفسيره، واخترت المتغيرات المناسبة التي يعتمد عليها هذا الحدث (ليس بالضرورة متغيرًا واحدًا – يمكنك اقتراح أكثر بحرية 🙂 ) فستستمتع بتحديد العلاقات (القوة والاتجاه) وكذلك بحساب «قيم جديدة» عمليًا.
قد تدهشك النتائج 🙂
النهاية
اضغط هنا لتتعرف على ما هو النموذج الاقتصادي القياسي (المحاضرة التالية) –>
اضغط هنا للعودة إلى صفحة المحاضرات في الاقتصاد القياسي
