كمية – لكن في الحقيقة لم يكن هناك …
حسنًا ، لست متأكدًا بنسبة 100٪ مما إذا كانت الكميات لا تزال موجودة في المدرسة الثانوية بعد التخفيضات السنوية المنتظمة للمواد. لا أريد حتى التحقق ، لأنني لماذا أغضب نفسي.
يجب أن يكونوا لا يزالون في الملف الشخصي الموسع. حقًا يجب أن يكونوا كذلك.
حسنًا ، لكن لماذا يحتاج أي شخص إلى هذا؟
في معظم التعريفات والنظريات الرياضية ، تُستخدم مفاهيم مثل: “كل” و “يوجد”.
عادةً ما تكون في تسلسلات أكثر تعقيدًا ، على سبيل المثال “بين كل رقمين توجد أرقام لا نهائية” (هذا نوع من نصف رسمي وغير دقيق إلى حد ما) ، أو: “لكل رقم حقيقي غير سالب يوجد بالضبط جذر واحد له”، أو: “يوجد شيء ما ، أنه لكل شيء آخر يوجد شيء آخر” (هذا هو التعريف الرياضي لشيء آخر).
في الكلية ستحصل على مجموعة كاملة من التعريفات والنظريات المقدمة بهذه الطريقة، يتم الإملاء عليها بسرعة في المحاضرة، أو – والأسوأ – مكتوبة مباشرة على السبورة في شكل:
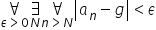
لذا سيكون من الجيد (بدلاً من رفع يدك وسؤال الأستاذ عما إذا كان يجب عليك “إعادة الرسم”) أن تكون قد تعلمت بالفعل كيفية قراءة هذه الصيغ بشكل صحيح. يمكنك بعد ذلك الانتقال مباشرة إلى مراحل “الغوص” في التعريف، وبعض الملاحظات حول كيفية عمله على أمثلة محددة، وما إلى ذلك.
المُحدِد العام والمحدد الخاص – دعونا نتعرف عليهما
“كل”، “لكل” – هذا هو المُحدِد العام، يُرمز إليه بـ: ![]() .
.
“يوجد”، “يوجد شيء ما” – هذا هو المُحدِد الخاص، يُرمز إليه بـ: ![]() .
.
أستخدم وأوصي بهذه الرموز لتسجيل الكميات لأنها لن تكون خاطئة مع بعضها البعض.
![]() – هو حرف A مقلوب (من الإنجليزية “all” – كل).
– هو حرف A مقلوب (من الإنجليزية “all” – كل).
![]() – هو حرف E مقلوب (من الإنجليزية “exists” – يوجد).
– هو حرف E مقلوب (من الإنجليزية “exists” – يوجد).
توجد أيضًا رموز أخرى للمحددات: Λ (“لكل”) و V (“يوجد”) – لكنني لن أتعامل معها، لأنها تختلط مع بعضها البعض.
الصيغ الرياضية المكتوبة باستخدام المحددات
أبسط الصيغ هي:
![]() – نقرأها: “لكل x” (يمكن أيضًا كتابتها:
– نقرأها: “لكل x” (يمكن أيضًا كتابتها: ![]() ، ولكنها تختلط مرة أخرى، لذا لن أفعل ذلك)
، ولكنها تختلط مرة أخرى، لذا لن أفعل ذلك)
![]() – نقرأها: “يوجد x”
– نقرأها: “يوجد x”
ومع ذلك، عادةً ما تكون الصيغ أكثر تعقيدًا، على سبيل المثال:
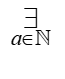 – نقرأها: “يوجد a عدد طبيعي”، أو: “يوجد شيء ما a، ينتمي إلى الأعداد الطبيعية”، أو أي تعبير آخر باللغة العربية يعبر عن جوهر الأمر، وهو:
– نقرأها: “يوجد a عدد طبيعي”، أو: “يوجد شيء ما a، ينتمي إلى الأعداد الطبيعية”، أو أي تعبير آخر باللغة العربية يعبر عن جوهر الأمر، وهو:
1. يوجد a
2. a عدد طبيعي
لا توجد هنا قواعد لغوية “صلبة” حول ما يجب أن تكون كل كلمة، سواء كان يجب أن تكون “يوجد a”، أو يجب أن تكون “يوجد شيء ما a”.
يمكن ويجب في الغالب، دمج الصيغ معًا، على سبيل المثال:
\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,تعني:
“لكل x>4 يوجد n ينتمي إلى الأعداد الطبيعية”
نفهم من ذلك أنه لكل x>4 “سنجد” n ينتمي إلى الأعداد الطبيعية، بحيث لكل x مثل هذا نختار n المناسب. الكميات تظل مرتبطة ببعضها البعض منطقياً، وليست صيغتين مستقلتين مكتوبتين بجانب بعضهما البعض.
أكثر من ذلك…
الترتيب له أهمية
نفس الصيغة كما في الصيغة الأخيرة، ولكن مع تغيير ترتيب الكميات:
\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,…سنقرأها بشكل مختلف:
“يوجد a عدد طبيعي، بحيث لكل x أكبر من 4…”
نفهم من ذلك أنه لدينا n في البداية (الذي نعلم بوجوده) وفقط لهذا n المحدد هناك شيء ما يحدث لكل x>4.
مثال – توضيح
المثال الكلاسيكي هنا هو تعريف التقارب الموحد والنقطي لتسلسل دالة، والذي يختلف فقط بترتيب الكميات (لقد قمت بتبسيط هذه التعريفات قليلاً):
التقارب النقطي:

التقارب الموحد:

في تعريف التقارب الموحد، انتهى الأمر بالكميات التي كانت في البداية في التقارب النقطي في النهاية. دون الخوض في التفاصيل، يغير هذا معنى الصيغة بأكملها.
في التقارب النقطي، في البداية (نقرأ من اليسار) أخذنا x معينًا، ثم قرأنا الصيغة وتوصلنا إلى أنه بالنسبة لهذا x المحدد، تقل المسافات بين قيم الدالة في التسلسل والدالة “الحدية” إلى اللانهاية.
في التقارب الموحد، في البداية قررنا أن المسافة بين القيم المناسبة للدوال تقل إلى اللانهاية، وبعد ذلك توصلنا إلى أن هذا يحدث لكل x.
كتابة التعريفات والنظريات
بمعرفة كيفية قراءة الكميات، فإن كتابة التعريفات والنظريات الرياضية تكون مفتوحة لنا. على سبيل المثال:
\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0سنقرأها كالتالي: “لكل عدد حقيقي x، x تربيع يكون أكبر من أو يساوي الصفر”، أو بطريقة أجمل: “كل عدد x مرفوع إلى التربيع غير سالب” – بالتأكيد أنا مع قراءة التعريفات والنظريات بلغة أكثر لونًا.
الجملة أعلاه صحيحة. ليس لدينا أي مشكلة في كتابة الجمل الكاذبة أيضًا:
\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1نقرأها كالتالي: “يوجد عدد موجب a، بحيث لكل x أكبر من هذا a، a مقسومًا على هذا x يكون أكبر من 1″، وهو بالطبع كذب (لأن العدد الموجب المقسوم على الأكبر منه لن يكون أبدًا أكبر من 1 ولا يوجد مثل هذا العدد).
والآن مع تعريف الحد من التسلسل من المشاركة السابقة:

سنقرأها كالتالي (بإضافة بعض الشرح):
“لكل ![]() أكبر من الصفر سنجد رقمًا في التسلسل
أكبر من الصفر سنجد رقمًا في التسلسل ![]() ، بحيث لكل مصطلح في التسلسل
، بحيث لكل مصطلح في التسلسل ![]() الذي رقمه أكبر من
الذي رقمه أكبر من ![]() تكون المسافة (القيمة المطلقة هي المسافة) بين هذا المصطلح في التسلسل والحد
تكون المسافة (القيمة المطلقة هي المسافة) بين هذا المصطلح في التسلسل والحد ![]() أصغر من
أصغر من ![]() ”
”
يمكننا أيضًا استخدام لغة أكثر بشرية:
“مهما كانت المسافة ![]() صغيرة في البداية، سنجد رقمًا في التسلسل، بحيث تكون جميع المصطلحات التالية في هذا التسلسل أقرب إلى الحد
صغيرة في البداية، سنجد رقمًا في التسلسل، بحيث تكون جميع المصطلحات التالية في هذا التسلسل أقرب إلى الحد ![]() من المسافة المحددة في البداية
من المسافة المحددة في البداية ![]() ”
”