تعريف رتبة المصفوفة وما يترتب عليها
افترض أننا عرفنا رتبة المصفوفة كالتالي: “عدد الصفوف والأعمدة الخطية المستقلة في المصفوفة”. ما هي الخصائص التي تترتب على هذه التعريف مباشرة؟
أولاً، من الواضح أن رتبة المصفوفة يمكن أن تكون: 1، أو 4، أو أحياناً 0. ولكن بالتأكيد لن تكون: -4، أو ![]() .
.
حسنًا، هل هذا كل شيء؟
لكن هل هذا كل ما يمكن استنتاجه؟ لنأخذ مثلاً هذه المصفوفة:
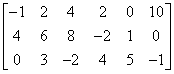
هذه المصفوفة تحتوي على 3 صفوف و6 أعمدة.
دعنا نسأل أنفسنا، ما هي رتبة هذه المصفوفة؟ هل يمكن أن تكون 7؟ من الواضح أنها لا يمكن أن تكون كذلك، لأن رتبة المصفوفة هي “عدد الصفوف والأعمدة الخطية المستقلة”، ولا يمكن أن تكون في هذه الحالة 7، لأن هذه المصفوفة لا تحتوي على هذا العدد من الصفوف أو الأعمدة!
والآن السؤال الأصعب… هل يمكن أن تكون الرتبة 6؟ المصفوفة تحتوي على 6 أعمدة…
الإجابة هي: لا. يجب أن تكون 6 هي “عدد الصفوف والأعمدة الخطية المستقلة”. يمكن أن تكون 6 عدد الأعمدة الخطية المستقلة (لأنها 6 أعمدة)، ولكن لا يمكن أن تكون عدد الصفوف الخطية المستقلة (لأنها فقط 3 صفوف). ويجب أن تكون عدد الصفوف والأعمدة الخطية المستقلة معًا.
من الواضح إذن أن رتبة هذه المصفوفة يمكن أن تكون بحد أقصى 3.
نصل هنا إلى خاصية مفيدة:
رتبة (A) <= الحد الأدنى (عدد الصفوف في المصفوفة، عدد الأعمدة في المصفوفة)
لذا، بالنظر إلى المصفوفة، يمكننا على الفور معرفة رتبتها الأقصى – وهو ما يكون مفيدًا في بعض الأحيان.
لحسابها بدقة أكبر، تحتاج إلى استخدام الطرق المناسبة – أظهرها في دورتي المخصصة للمصفوفات في الدرس الخامس، مرحبًا بك!


