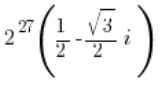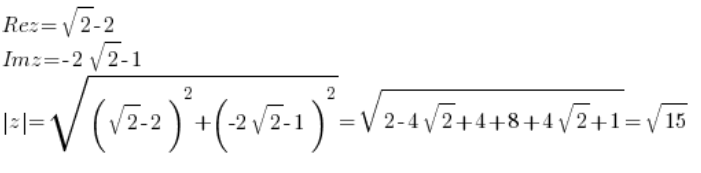الأعداد المركبة ككل ليست موضوعًا معقدًا وصعبًا. لكن “الحرارة” قد ترتفع في المواقف غير التقليدية والأقل نمطية. المفتاح في هذه الحالة – كما هو الحال دائمًا – هو فهم الموضوع و”الهدوء”، أي الصفاء الذهني والثقة بالنفس.
أمثلة
على سبيل المثال:
- عند رفع العدد المركب إلى قوة أكبر، غالبًا ما نحصل على شكل غريب نوعًا ما:
لتحسين جمالية الرقم، يمكن إجراء التحويل التالي:
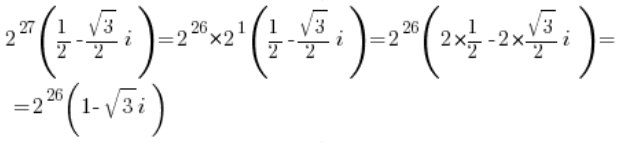
تحسين الجمالية مهم جدًا – خاصة إذا كان هذا الرقم جزءًا من كائن رياضي أكثر تعقيدًا. - العدد المركب بالشكل الديكارتي (أو: الجبري) لا يجب أن يكون جميلاً، مثل: . قد تكون جزئها الحقيقي والتخيلي قبيحة وغير منطقية، مثل:
لكن لا داعي للذعر، فهي مجرد عدد مركب، حيث (الجزء الحقيقي غير مضروب بـ ‘i’، والجزء التخيلي مضروب بـ ‘i’):
– تغيير الإشارة في الجزء التخيلي
. قد تكون جزئها الحقيقي والتخيلي قبيحة وغير منطقية، مثل:
– تغيير الإشارة في الجزء التخيلي
