حجم القطع الناقص (لكن ليس الدوراني، بل من النوع البري) المحسوب بالتكامل المحدد

---

لنقل إننا بحاجة لحساب حجم القطع الناقص:

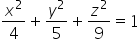
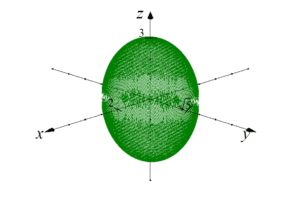
هذا هو القطع الناقص الذي يتقاطع مع محاور x,y,z عند الإحداثيات 2، و3 (المعادلة العامة للقطع الناقص هي: 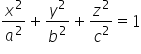, حيث a,b,c هي إحداثيات التقاطع).

ليس هذا قطعًا ناقصًا دوارًا، لم يتكون بدوران أي منحنى حول أي محور، لا يمكننا استخدام الصيغة القياسية لحجم الجسم الدوار:

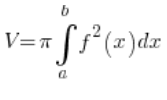
علينا إيجاد طريقة أخرى.

1. نختار أي نقطة M(z) في وسط القطع الناقص وعلى محور OZ.

المستوى الذي يمر عبر هذه النقطة وعمودي على محور OZ “يقطع” لنا قطعًا ناقصًا معينًا من القطع الناقص:

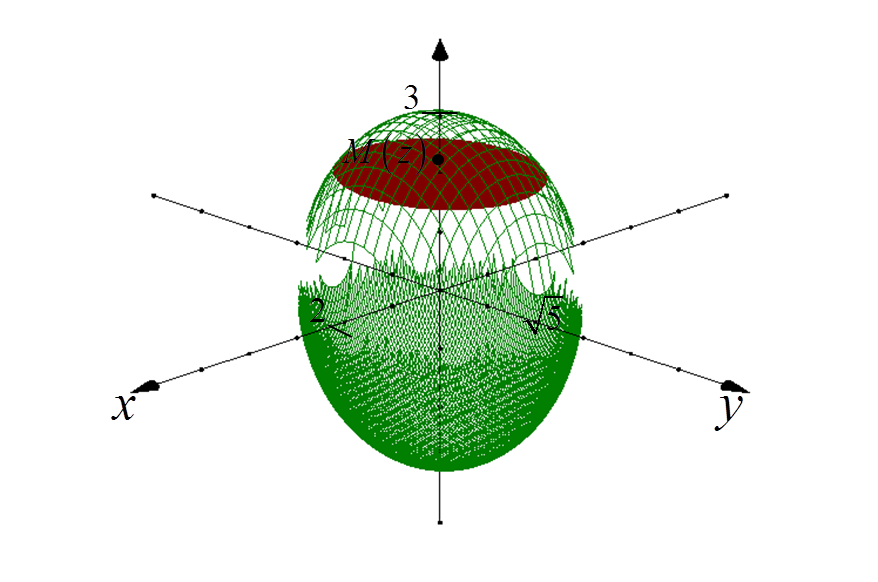
2. نحدد معادلة إسقاط القطع الناقص “المقطوع” على مستوى XY

نحدد معادلة هذا القطع الناقص، لموقع محدد ‘z’ (نعامل ‘z’ كأنه ثابت) من المعادلة العامة للقطع الناقص:

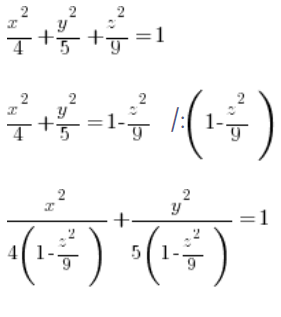
يمكننا رؤية أن ‘a’ و’b’ من المعادلة العامة للقطع الناقص (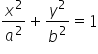) هي:

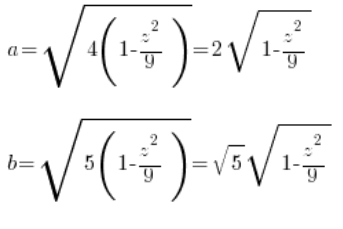
4. نحسب مساحة هذا المقطع بناءً على المتغير ‘z’

مساحة هذا القطع الناقص تعتمد على النقطة ‘z’ المختارة، وبالتالي ستكون كأنها دالة للمتغير ‘z’. يمكننا حسابها إما باستخدام الصيغة الجاهزة لمساحة القطع الناقص ():

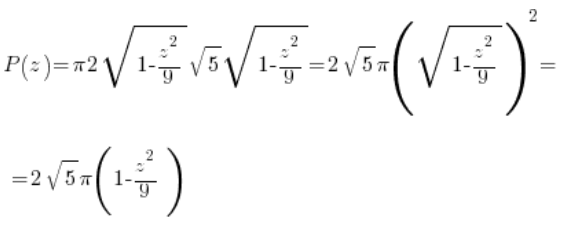
أو بحساب التكامل المحدد المناسب (باستخدام بالتأكيد الشكل البارامتري للقطع الناقص والصيغة لمساحة المنطقة بالشكل البارامتري):

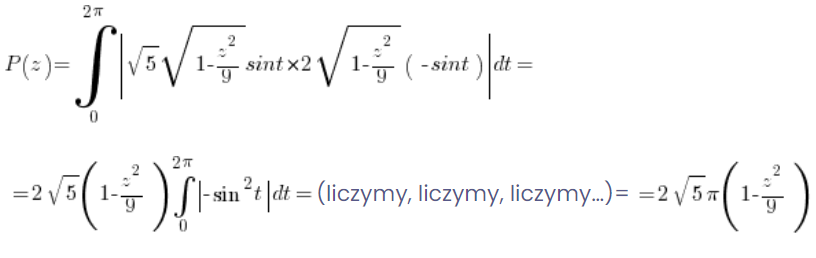
5. نحسب حجم الجسم باستخدام مساحات المقاطع

الآن تأتي اللحظة الصعبة. حجم الجسم يساوي – وهذا يبدو غير جميل قليلاً – “مجموع” (أي تكامل) جميع المقاطع، بشكل عام:

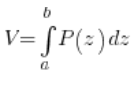
حيث هي دالة مساحات المقاطع للجسم بمستوى عمودي على محور OZ، و’a’ و’b’ هما الحدود التي يتغير فيها ‘z’.

يعني في حالتنا:

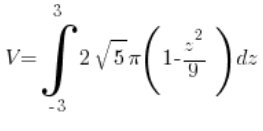=(نحسب، نحسب، نحسب…)=

وهذا يتوافق مع الصيغة العامة للقطع الناقص ().

النهاية

من المهم تذكر هذا المخطط العام والأهم من ذلك هو أن حجم الأجسام الصعبة، غير الدوارة يمكن حسابه بتكامل دالة مساحات مقاطعها.