تلخيص تحويلات أويلر من النوع الثالث

---

تحويلات أويلر من النوع الأول والثاني والثالث – لا حاجة إلى المزيد

في المنشورات السابقة، أظهرت كيفية استخدام تحويلات أويلر في تكاملات من النوع:

• تحويلات أويلر من النوع الأول (عندما a>0)
• تحويلات أويلر من النوع الثاني (عندما c>0)

في هذا المنشور سنتناول النوع الثالث والأخير من تحويلات أويلر التي يمكننا استخدامها عندما يكون في التكامل:

المعادلة التربيعية , لها جذور مختلفة ، أي عندما يكون ، أي عندما يمكن كتابتها في شكل الضرب: .

ولكن قبل أن ننتقل إلى الأمور العملية، لنلاحظ أن هذه الحالات الثلاث:

• النوع الأول، عندما a>0
• النوع الثاني، عندما c>0
• النوع الثالث عندما يكون هناك جذور مختلفة

ستسمح لنا بحل أي تكامل من النوع:

في الواقع، النوع الأول والثالث فقط يكفيان.

لماذا؟

الحالة، عندما يمكننا تجاهلها، لأن المعادلة التربيعية تتحول ببساطة إلى الشكل الخطي ، والتي يمكننا حلها باستخدام تحويلات أبسط من تحويلات أويلر.

ماذا عن الحالة عندما a<0 (لا يتناسب مع النوع الأول) والمعادلة التربيعية لها جذر واحد أو ليس لها جذور على الإطلاق (لا يتناسب مع النوع الثالث)؟

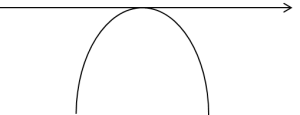
حينها سيكون شكل الرسم البياني لها كالتالي (نتذكر من المدرسة الثانوية – الأذرع إلى الأسفل):

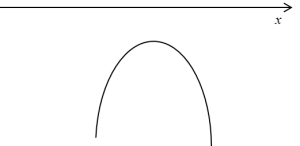
أو، إذا لم يكن لها جذور على الإطلاق، كالتالي:

ما هو الدرس المستفاد؟ أن في كلتا الحالتين المعادلة التربيعية كانت ستأخذ قيمًا سالبة (باستثناء، على الأكثر، نقطة واحدة)، وأذكركم أننا نحسب التكامل:

أي أن المعادلة التربيعية تحت الجذر، والجذر لا يمكن حسابه من القيم السالبة (نحن نتعامل مع الأعداد الحقيقية، بالطبع). أي أن مجال هذه الدالة سيكون على الأكثر نقطة واحدة، مما يجعلها غير منطقية ولن نحصل على مثال كهذا بالتأكيد. إلا إذا كان الأستاذ متعباً جداً عند إعداد الأمثلة للاختبار.

لذلك، يمكن تجاهل الحالة عندما a<0 والمعادلة التربيعية ليس لها جذورين مختلفين ومن الواضح الآن أن النوع الأول والثالث من تحويلات أويلر يتناسبان مع أي تكامل من النوع:

إذن، لنبدأ الآن بالنوع الثالث من تحويلات أويلر.

تحويلات أويلر من النوع الثالث

لدينا تكامل:

,

حيث له ، أي يمكن كتابتها على شكل:

,

حيث هي جذورها.

التحويل الذي نستخدمه هنا هو:

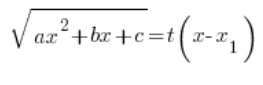
نرفع هذا التحويل إلى مربع، نكتب المعادلة التربيعية في الجانب الأيسر في شكل الضرب (نعرف أنه يمكن)، نقسم الطرفين على ونستمر كما في أنواع التحويلات السابقة، نحدد بالتتابع:

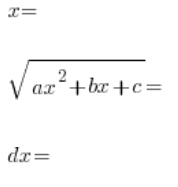
وفي النهاية نضع كل شيء في التكامل الأصلي ونخرج إلى تكامل كسري – عادة ما يكون مرهقًا.

لنبدأ.

مثال

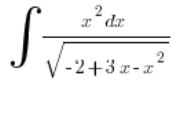
لدينا (أي a<0، أي لن نستخدم تحويلات النوع الأول)، لدينا (أي c<0، أي لن نستخدم تحويلات النوع الثاني)، ولكن لدينا ، أي يمكننا استخدام تحويلات النوع الثالث.

نحسب في البداية :

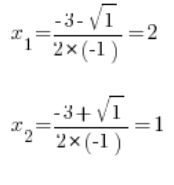
نستخدم تحويل أويلر من النوع الثالث:

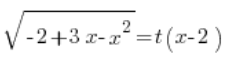
نرفع الطرفين إلى مربع:

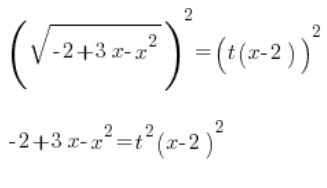
نكتب المعادلة التربيعية في الجانب الأيسر في شكل الضرب (تذكروا هنا!!!):

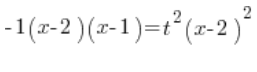
نقسم الطرفين على :

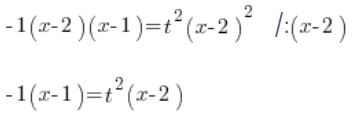
نحدد :

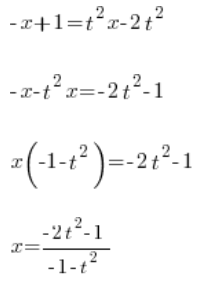
لدينا محددة باستخدام المتغير . الآن نحدد .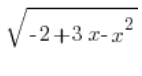

بالعودة إلى تحويلنا الأول لدينا أن:

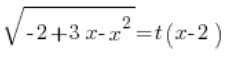
نضع 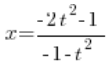المحددة ولدينا:

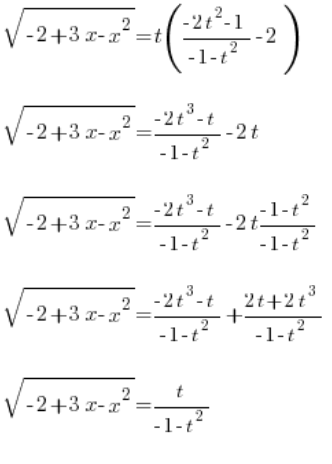
لدينا 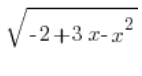محددة بشكل جميل. الآن بقي فقط ، والتي سنحسبها بحساب المشتقة لـ :

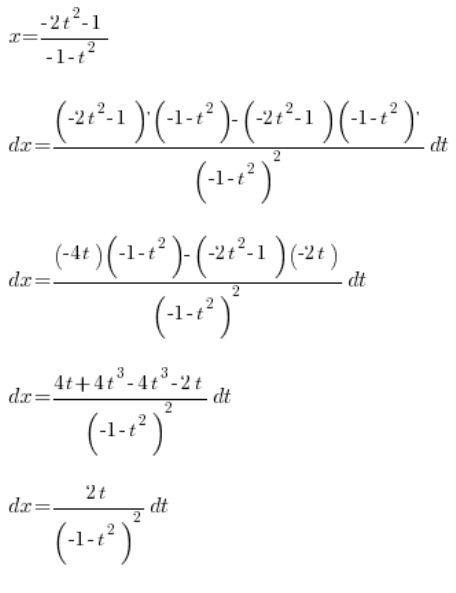
لذا لدينا:

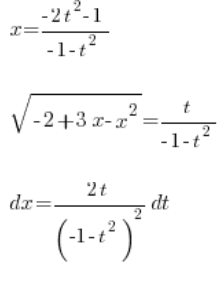
، كل شيء باستخدام المتغير . نضع هذا في التكامل:

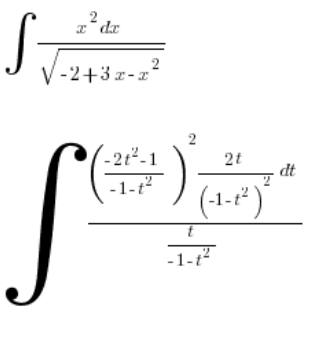
نبسط:

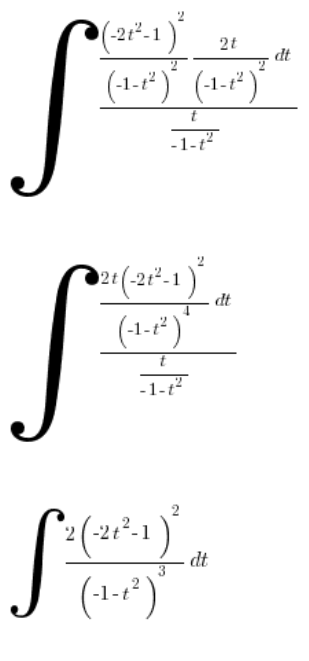
كما توقعنا، نحصل على تكامل كسري معقد، لن نقوم بحسابه الآن.

أخيراً، يجب ملاحظة أن…

ملاحظة حول تحويلات أويلر

لدينا تكامل:

  ,

حيث:

• النوع الأول، عندما a>0
• النوع الثاني، عندما c>0
• النوع الثالث عندما يكون هناك جذور مختلفة

من الواضح أنه غالباً ما يمكن حله باستخدام أحد تحويلات أويلر، أو حتى أي منها (عندما a>0، c>0 وفي نفس الوقت ).

لا توجد مشكلة، على الرغم من أنه من السهل حسابياً أن أوصي باستخدام النوع الأول أولاً، وإذا لم يكن ممكناً، فالننوع الثاني، وإذا لم يكن ممكناً، فالننوع الثالث.

هذا كل شيء عن استخدام تحويلات أويلر، أتمنى أن يكون ذلك مفيداً لكم في الجامعة، وكالعادة، أدعوكم إلى التعليقات أسفل المنشور.