بعض الأشياء التي يجب أن تتعلمها جيدًا في المدرسة الثانوية ولكن لم يخبرك بها أحد – الجزء 3: الدالة التربيعية

هذا المنشور هو الثالث على التوالي، حيث أود أن ألفت انتباهك إلى الأشياء التي تستحق المراجعة في بداية دراستك للرياضيات في الجامعة. مراجعتها بسرعة ستسهل حياتك الدراسية كثيرًا. في المنشورات السابقة تناولت مواضيع:

التفسير الهندسي للقيمة المطلقة

الكميات

اليوم جاء دور الدالة التربيعية.

دالة تربيعية؟ لكننا قمنا بها لمدة شهرين على ما أظن…

موضوع الدالة التربيعية بالطبع واسع جدًا ولا أقصد أنك تأخذ الكتاب المدرسي من الثانوية وتدرس الفصل بالكامل من الغلاف إلى الغلاف.

لنتوقف فقط عند بعض التفاصيل الهامة، الفروق الصغيرة والفخاخ.

الدالة التربيعية والمعادلة التربيعية

الدالة التربيعية هي بالطبع شيء مثل هذا:

أو: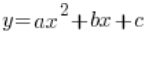

حيث هي أرقام عشوائية. أمثلة على الدوال التربيعية هي:

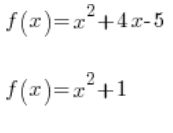
وغيرها…

مفهوم الدالة التربيعية يجب أن يختلف عن مفهوم المعادلة التربيعية، على سبيل المثال:

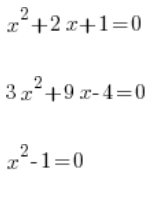
وغيرها…

هذا ليس نفس الشيء!!!!

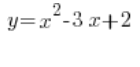هي دالة تربيعية، بينما 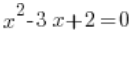هي معادلة تربيعية.

عدم التفرقة بين الدالة والمعادلة يؤدي غالبًا إلى…

الخطأ الفادح رقم 1

عند حساب المشتقات مثلاً وعند إعطاء دالة معينة:

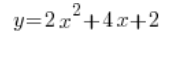
الناس غالبًا ما يفعلون شيء مثل هذا:

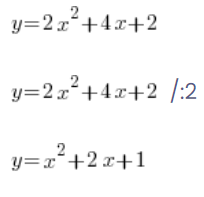
…ويستمرون في الحسابات المطلوبة.

يخطئون بهذا الشكل لأنهم يتذكرون أنه كان بالإمكان فعل شيء مماثل في المعادلات:

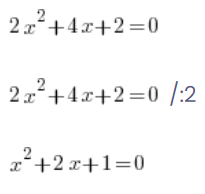
…وفي المعادلة كل شيء على ما يرام، يمكن القسمة على الطرفين، 0 في الجهة اليمنى مقسومة على 2 يعطي بالفعل 0 والمعادلات تكون متكافئة (لها نفس الحلول).

لكن هذا الرقم لا يمكن تنفيذه على الدوال – يجب على الأقل قسمة اليسار أيضًا على y إلخ. بعد قسمة قيمة الدالة على 2 ستحصل على دالة مختلفة تمامًا!

ماذا يجب أن تراجع من الدوال؟

ليس الكثير. في الواقع فقط شكلين من الدوال: الشكل القياسي والشكل المضاعف.

الشكل القياسي للدالة التربيعية

أفترض أن الشكل العام للدالة التربيعية نعرفه:

شكلها القياسي هو:

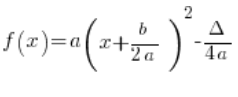
أي:

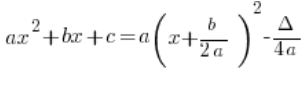
ما هو a و b و معروف، قليل من الناس لديهم مشكلة مع .

يمكن حتى ملاحظة أنه إذا سحبنا من الشكل القياسي، سنحصل على:

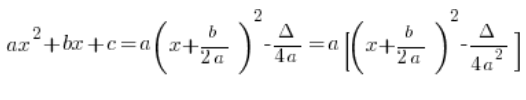
…ما يمكن أن يكون مفيدًا أحيانًا، وأحيانًا ليس بالضرورة.

إذا كنت تعلمت هذا بحساب إحداثيات الرأس (عادةً و ) وإدخالها في الصيغة:

فبالطبع هذا قليل من الالتفاف، لكنه أيضًا جيد.

تذكر في بداية الصيغة القياسية!

الشكل المضاعف للدالة التربيعية (تفكيكها إلى عوامل):

بالعودة الآن إلى دالتنا التربيعية العامة:

غالبًا ما ستحتاج إلى “تفكيكها إلى عوامل”، باستخدام الشكل المضاعف للدالة التربيعية:

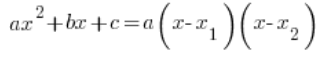
حيث و نحسب من الصيغ المعروفة والمحبوبة:

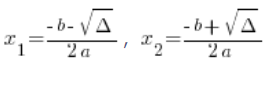
هنا أيضًا يجب أن تتذكر في بداية الصيغة!!!

لاحظ أيضًا أن هذه و لا توجد دائمًا (إذا كانت دلتا سلبية، فهي غير موجودة)، أي أن الدالة لا يمكن دائمًا كتابتها في شكل مضاعف، أي أن الدالة التربيعية لا يمكن تفكيكها إلى عوامل دائمًا.

ماذا يجب أن تراجع من المعادلات التربيعية؟

مع المعادلات التربيعية أعتقد أن الأمور ليست سيئة للغاية. نحن عادة نعرف كيفية حل المعادلة العامة:

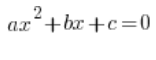
على سبيل المثال:

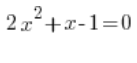
نحسب ببساطة:

ثم، إذا كانت دلتا غير سلبية، حلول المعادلة:

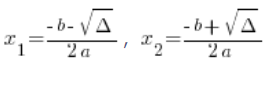
تذكر أنه في المقام هناك وليس فقط 2!

أود التوقف عند الحالة الخاصة للمعادلة:

هنا تحدث العديد من الأخطاء. على سبيل المثال:

الخطأ الفادح رقم 2

ما هو الخطأ بالضبط؟ الرقم 2 هو بالفعل حل المعادلة ، لكن تم إهمال الحل الثاني لهذا المعادلة، وهو الرقم -2. يجب أن يكون:

يمكن تجاهل الحل السلبي فقط في الهندسة (لأن المسافة لا يمكن أن تكون سلبية).

مشكلة أخرى مع المعادلة في الشكل: هي:

الخطأ الفادح رقم 3

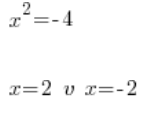
وهو بالطبع هراء، لأن 2 تربيع لا يعطي -4. في الواقع لا شيء تربيع يعطي -4 (أولئك الذين درسوا الأعداد المركبة فليصمتوا). المعادلة:

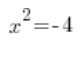
…ليس لها أي حلول.

لذا يجب أن تكون يقظًا. المعادلة لها حلان، والمعادلة ليس لها أي حلول.

أدعوكم إلى مراجعة كل ما قيل حتى الآن بهدوء وبالطبع إلى طرح الأسئلة في التعليقات.