اختزال بعض المعادلات من الدرجة الرابعة إلى معادلات تربيعية
العديد من المعادلات الحدودية من الدرجة الرابعة يمكن تحويلها إلى معادلات تربيعية باستخدام الحيلة المعروفة جيدًا من المدرسة الثانوية الموضحة هنا:
هذا ينطبق بالطبع أيضًا على المعادلات الحدودية بالأعداد المركبة.
أذكركم، الفكرة هي أن لدينا معادلة:
{{z}^{4}}+3{{z}^{2}}+2=0نقوم بتبديل: {{z}^{2}}=t
ونصل إلى معادلة تربيعية:
{{t}^{2}}+3{t}+2=0ثم نقوم بحلها باستخدام دلتا العادية وما إلى ذلك، نحصل على الحلول ![]() , مع تذكر أن
, مع تذكر أن ![]() نكون منها معادلتين إضافيتين:
نكون منها معادلتين إضافيتين:
![]() أو
أو ![]()
نحلها ونحصل على أربعة حلول: ![]() .
.
اختزال بعض المعادلات من درجات أكبر إلى معادلات تربيعية
لا يوجد أي مانع على الإطلاق من توسيع هذه الطريقة لتشمل المعادلات من درجات أكبر من 4 (إذا كان بالإمكان تحويلها إلى تربيعية عن طريق التبديل).
إذًا لدينا:
2{{z}^{6}}-5{{z}^{3}}+4=0يمكن أيضًا ملاحظة أنه يعادل:
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0وبعد التبديل: ![]()
نصل إلى معادلة تربيعية:
2{{t}^{2}}-5t+4=0في المعادلة:
{{x}^{10}}-3{{x}^{5}}+1=0بعد التبديل: ![]()
نحصل على:
{{t}^{2}}-3t+1=0وهكذا دواليك…
مثال
لنأخذ المعادلة:
z^6+(1-i)z^3-i=0نقوم بتبديل z^2=t ولدينا:
t^2+(1-i)t-i=0ثم نتابع الحساب:
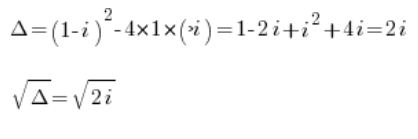
نحسب هذه الجذور باستخدام الطرق المعروفة للأعداد المركبة (الموضحة مثلا في دورتي).
لدينا ![]() أو
أو ![]()
يعني:
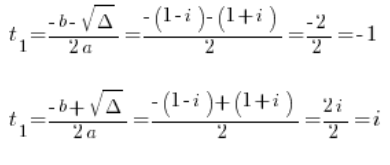
نذكر أن هذه ليست حلولًا بعد، لأن z^3=t
يعني لدينا لحل المعادلات:
z^3=-1وكذلك:
z^3=iنحولها إلى:
![]() وكذلك
وكذلك ![]()
وباستخدام الطرق المعروفة نحسب ثلاث جذور من المعادلة الأولى:
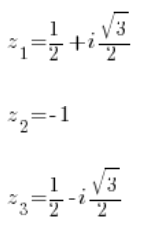
وكذلك ثلاث جذور من المعادلة الثانية:
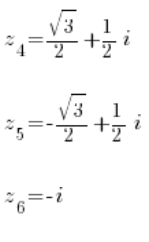
تم الحل 🙂


