المعادلات الكثيرة الحدود من الدرجة الرابعة في الأعداد المركبة

عند حل المسائل باستخدام المعادلات الكثيرة الحدود المركبة، نستخدم عمومًا نفس الطرق التي نستخدمها في حل المسائل بالمعادلات الكثيرة الحدود الحقيقية في المدرسة الثانوية.

المعادلات المركبة من الدرجة الرابعة التي يمكن تقليصها إلى الدرجة الثانية

وينطبق هذا أيضًا على المعادلات المركبة من الدرجة الرابعة التي يمكن تقليصها إلى المعادلات من الدرجة الثانية، أي تلك التي لدينا فيها متغير إلى القوة الرابعة، ومتغير إلى القوة الثانية وحد ثابت، على سبيل المثال:

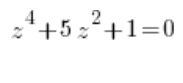
أو:

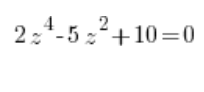
نحول هذا النوع من المعادلات المركبة إلى معادلات مركبة من الدرجة الثانية من خلال الاستبدال ، حيث هي بالطبع المتغير المركب.

المهمة

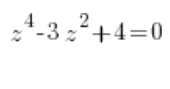
نقوم بالاستبدال (بالطبع 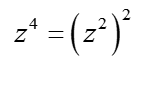)، فنحصل إذًا:

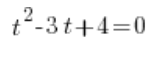
وبالتالي نحل هذه المعادلة بالطريقة العادية باستخدام دلتا (بالطبع، جذور الأعداد السالبة موجودة في الأعداد المركبة). سنحصل على حلين مركبين:

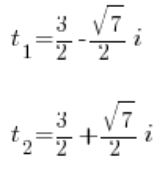
بما أننا قمنا بالاستبدال: ، لدينا:

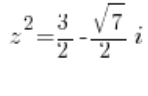
أو:

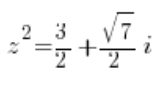
أي:

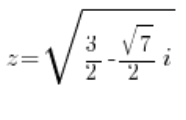
أو:

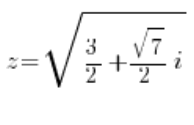
بعد حساب الجذور (بالطبع ستكون أربع جذور مركبة) سيكون لدينا أربع حلول:

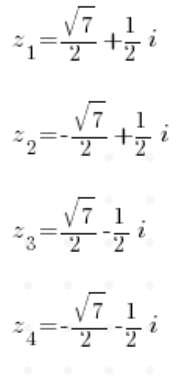
ملاحظة: أعرض هذه وطرق أخرى في الدرس 6 من دورة الأعداد المركبة، أدعوكم لزيارتها!