تأتيني الكثير من الأسئلة حول الصيغة التي قدمتها في دورة التكاملات غير المحدودة للصيغة المعيارية للدالة التربيعية.
الصيغة:
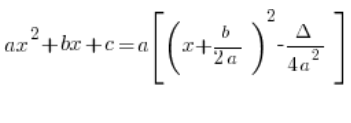
تظهر في مخطط حل التكاملات الجذرية في الدرس الخامس من الدورة:
لماذا هناك a^2؟
المشكلة هي أنه في النظرة الأولى يبدو مختلفًا عن الصيغة المعيارية المعروفة من المدرسة الثانوية:
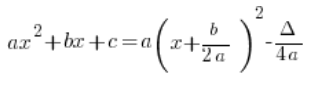
السؤال المعتاد هنا هو: “لماذا لديك 
في المقام؟”
تحويل الصيغة
يكفي أن تلاحظ أنه إذا في الصيغة:
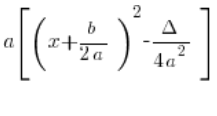
نضرب 
في القوس المربع، نحصل على الصيغة بالضبط:
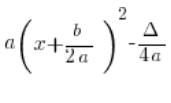
(بعد ضرب في العامل 
، يختصر ونصل إلى 
)
لذا فإن كلا الشكلين متكافئين، أي ببساطة:
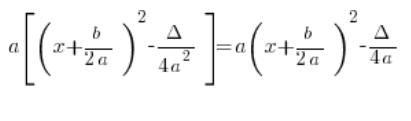
إذن لماذا نقدم هذه الصيغة بالقوس المربع و a خارج القوس؟ لأنه في التكاملات الجذرية يكون ذلك أسهل 🙂
في المراحل التالية من حساب التكامل، ستحتاج إلى استخراج أمام علامة التكامل (وأولاً أمام القوس في المقام)، فلماذا الانتظار؟ 🙂
