تحدث في الحياة مواقف عندما تكون منطقة التكامل في التكامل الثنائي هي الإهليلج….
ماذا نفعل في هذه الحالة؟
الإحداثيات الإهليلجية
طريقة أنيقة للحل هي عادة استخدام ما يسمى بالإحداثيات الإهليلجية. هذا يشبه إلى حد كبير الإحداثيات القطبية، آلية العمل مشابهة تمامًا، فقط تستبدل x و y بشيء آخر ويكون الجاكوبي مختلفًا. تفسير ‘r’ أيضًا مختلف. لذلك، إذا كنت تعرف كيفية التحويل إلى الإحداثيات القطبية (ويتم ذلك غالبًا عندما تكون منطقة التكامل هي دائرة) فسوف تفهم بسهولة الإحداثيات الإهليلجية أيضًا.
لذلك لدينا التكامل: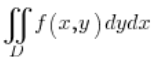 
ومنطقة التكامل محدودة بإهليلج مركزه في نقطة الأصل، ومعادلته هي: 
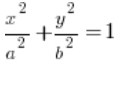. دعنا نتأكد من أن الرقم 1 موجود على الجانب الأيمن من معادلة الإهليلج، حسنًا؟ إذا كان الرقم على سبيل المثال 9، يمكنك جعله بسهولة 1 عن طريق قسمة كلا الجانبين من المعادلة على 9.
منطقة التكامل المرسومة تبدو هكذا:
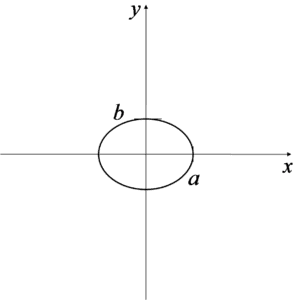
ماذا تعني a و b واضح في الرسم. يجب الانتباه، لأنه إذا كان في مقام معادلة الإهليلج تحت 
على سبيل المثال 9، فهذا يعني أن 
، من الواضح لماذا، أليس كذلك؟
الآن بعد أن أصبحت لدينا هذه “الوضعية النقية”، ننتقل إلى الإحداثيات الإهليلجية، ونستبدل:
معنى المتغيرات في الإحداثيات الإهليلجية
الزاوية 
تعني بالضبط نفس ما تعنيه في الإحداثيات القطبية، و 
تعني شيئًا مختلفًا. في المسائل الأساسية للإهليلج الذي يعطى بمعادلة جميلة 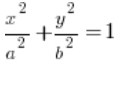افترض ببساطة أن يتغير من الصفر إلى الواحد (في الحالات الأكثر تعقيدًا أدخل و إلى معادلة الإهليلج واحسب الحد العلوي لـ r).
الجاكوبي
الجاكوبي في الإحداثيات الإهليلجية يساوي 
.
بتذكر الجاكوبي ننتقل إذًا إلى التكامل في الإحداثيات الإهليلجية:
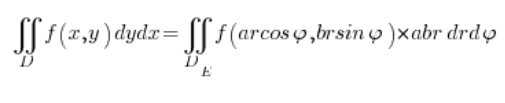
حيث المتغيرات و مقيدة: في الحدود من الصفر إلى الواحد، و حسب ما إذا كنا نتحدث عن الإهليلج كله، أو نصفه، أو ربع الإهليلج مثلًا – كما في الإحداثيات القطبية.
فقط خذ وابدأ الحساب.
مثال
احسب التكامل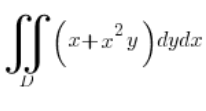 
، حيث D هو الإهليلج بمعادلة: 
.
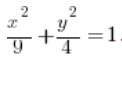وفقًا للنظام السابق، نستبدل:
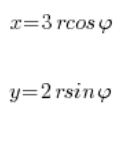
نأخذ منطقة التكامل:
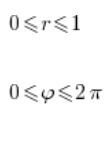
ونحسب التكامل:
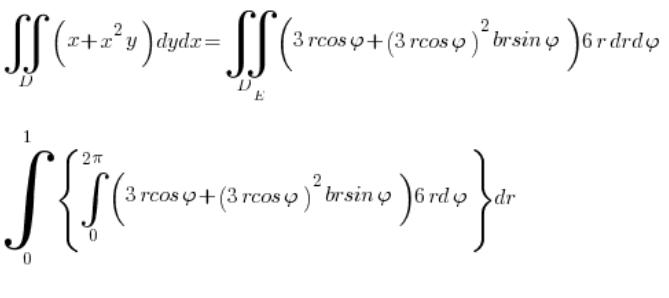
الذي بالطبع أصبح إجراءً شكليًا 🙂
