 Co robić z wartościami bezwzględnymi w całkach? Co robić z wartościami bezwzględnymi w ogóle?
Co robić z wartościami bezwzględnymi w całkach? Co robić z wartościami bezwzględnymi w ogóle?
Odpowiedź jest dosyć prosta i wynikająca z ogólnej definicji wartości bezwzględnej.
No dobra, no to co to jest ta wartość bezwzględna?
Oczywiście, żeby coś włożyć, trzeba najpierw wyjąć.
Wyrzuć więc z głowy wszystkie podstawówkowe „regułki” i skojarzenia typu: „wartość bezwzględna to jest takie coś, że się pisze coś zawsze z plusem i się nie pisze minusa”.
Nie.
Poprawnie rzecz biorąc, wartość bezwzględna to funkcja, która może przyjmować różne wartości (także, co jest dla niektórych szokujące, wartości „z minusem”), w zależności od argumentu, według „przepisu”:
\left| x \right|=\left\{ \begin{matrix}& x\quad dla\ x\ge 0 \\& -x\ \,dla\ x<0 \end{matrix} \right.Czyli:
- Jeżeli wartość bezwzględna jest liczona z czegoś (bardziej fachowo: z argumentu) nieujemnego, jest równa temu czemuś (argumentowi).
- Jeżeli wartość bezwzględna jest liczona z czegoś ujemnego, jest równa temu czemuś ze znakiem minus.
Przykłady
\left| 5 \right|=5, bo 5 jest nieujemne.
\left| -1 \right|=-\left( -1 \right), bo -1 jest ujemne.
A co jeśli wartość bezwzględna jest liczona z \left| x+1 \right|?
Wartość bezwzględna liczona ze zmiennych
Czy możesz, sobie „przyjąć”, że x+1 jest „dodatnie” (bo ma plus z przodu), czyli, że \left| x+1 \right|=x+1?
No oczywiście, że nie.
Wyrażenie x+1 jest raz dodatnie (jeśli za x podstawimy np. 20 i będziemy mieli x+1=20+1=21), a dla innych wartości x ujemne (jeśli za x podstawimy np. -2 i będziemy mieli -2+1=-2+1=-1).
Wychodzi więc, że wartość bezwzględna z x+1 dla jednych argumentów x przyjmuje wartość x+1, a dla innych przyjmuje wartość -(x+1).
Czyli:
- Jeżeli x+1\ge 0, to \left| x+1 \right|=x+1.
- Jeżeli x+1<0, to \left| x+1 \right|=-\left( x+1 \right)
Określenie natomiast, gdzie x+1\ge 0, a gdzie x+1<0 nie stanowi – od czasów podstawówki – problemu:
x+1\ge 0 x\ge -1oraz:
x+1<0 x<-1Czyli:
- Jeżeli x\ge -1, to \left| x+1 \right|=x+1.
- Jeżeli x<-1, to \left| x+1 \right|=-\left( x+1 \right)
Co można podsumować zgrabnym wzorem:
\left| x+1 \right|=\left\{ \begin{matrix}& x+1\quad dla\ x\ge -1 \\& -\left( x+1 \right)\ \,dla\ x<1 \end{matrix} \right.Jeżeli teraz ta wartość bezwzględna \left| x+1 \right| była nam do czegoś potrzebna (np. była wyrażeniem podcałkowym w całce), należy rozbić dalsze zadanie na przypadki. Pierwszy przypadek to ten, w którym zakładasz, że x\ge -1 i odpowiednio „opuszczamy” wartość bezwzględną. Drugi przypadek to ten, w którym zakładasz, że x<-1 i również odpowiednio „opuszczamy” wartość bezwzględną.
Na końcu ładnie spinasz oba przypadki – ale nie na siłę, tylko wtedy, gdy jest to możliwe.
Podsumowanie – ogólny schemat
Ogólny schemat wyglądał by więc tak:
- Określasz, w jakich przedziałach wyrażenie pod wartością bezwzględną przyjmuje wartości nieujemne, a w jakich ujemne.
- Rozbijasz zadanie na przypadki i odpowiednio pomijasz wartość bezwzględną (ze znakiem + lub -).
- Piszesz odpowiedź.
Uwaga
Krok 1 nie musi być wcale taki prosty, jak powyżej, niestety…
Przykład 1
Masz do policzenia całkę: \int{\left| x-2 \right|dx}.
Krok 1
Określasz, gdzie x-2\ge 0, a gdzie x-2<0.
\begin{matrix}& x-2\ge 0 \\& x\ge 2 \end{matrix}No i:
\begin{matrix}& x-2<0 \\& x<2 \end{matrix}Krok 2
Twoje przypadki, na które musisz rozbić zadanie to:
Przypadek 1
Zakładam, że x\ge 2, czyli, że: x\in <2,\infty ). Przy tym założeniu:
\int{\left| x-2 \right|dx}=\int{\left( x-2 \right)dx}=\int{xdx}-\int{2dx}=\frac{1}{2}{{x}^{2}}-2x+C (jak liczy się całki możesz nauczyć się z mojego Kursu Video o całkach nieoznaczonych)
Przypadek 2
Zakładam, że x< 2, czyli, że: x\in <-\infty ,2). Przy tym założeniu:
\int{\left| x-2 \right|dx}=\int{-\left( x-2 \right)dx}=-\int{xdx}+\int{2dx}=-\frac{1}{2}{{x}^{2}}+2x+CKrok 3
Odpowiedzi w obu przypadkach możesz zgrabnie „spiąć” wzorem:
\int{\left| x-2 \right|dx=\left\{ \begin{matrix}& \frac{1}{2}{{x}^{2}}-2x+C\quad dla\ x\in <2,\infty ) \\& -\frac{1}{2}{{x}^{2}}+2x+C\quad dla\ x\in <-\infty ,2) \end{matrix} \right.}Albo jeszcze bardziej zaszpanować i użyć funkcji "sgn":
\int{\left| x-2 \right|dx}=sgn \left( x-2 \right)\left( \frac{1}{2}{{x}^{2}}-2x \right)+C…która zwraca wartość +1, lub -1, w zależności od znaku argumentu.
Przykład 2
Policz całkę: \int\limits_{0}^{2}{\left| x-1 \right|dx}.
Krok 1
Określasz, gdzie x-1\ge 0, a gdzie x-1<0.
x-1\ge 0 x\ge 1oraz:
x-1<0 x<1Krok 2
Jak już na pewno rozumiesz, wartość bezwzględną musisz „opuścić” ze znakiem + tam, gdzie x\ge 1 i ze znakiem – tam, gdzie x<1.
Całka oznaczona jednak ma swoją specyfikę, różni się od nieoznaczonej. Liczysz ją w konkretnym przedziale x-sów. W tym przykładzie:
\int\limits_{0}^{2}{\left| x-1 \right|dx}Całkę oznaczoną liczysz dla x\in \left\langle 0,2 \right\rangle . Powstaje problem, jak właściwie masz „opuścić” znak wartości bezwzględnej, bo dla pewnych x-sów z tego przedziału musisz to zrobić tak, a dla innych inaczej. Rozwiązaniem jest rozbicie całki oznaczonej na dwie całki:
\int\limits_{0}^{2}{\left| x-1 \right|dx}=\int\limits_{0}^{1}{\left| x-1 \right|dx}+\int\limits_{1}^{2}{\left| x-1 \right|dx}Teraz wiadomo, że pierwszą z tych całek liczę TYLKO dla x\in \left\langle 0,1 \right\rangle , a dla takich x-sów, jak wiem z Kroku 1, argumenty wartości bezwzględnej są ujemne, mogę więc „opuścić” ją ze znakiem -.
Wiadomo też, że drugą z tych całek liczę TYLKO dla x\in \left\langle 1,2 \right\rangle , a dla tych x-sów, zgodnie z obliczeniami z Kroku 1, argumenty wartości bezwzględnej są dodatnie, „opuszczam” więc ją ze znakiem +.
Mam więc:
\int\limits_{0}^{2}{\left| x-1 \right|dx}=\int\limits_{0}^{1}{\left| x-1 \right|dx}+\int\limits_{1}^{2}{\left| x-1 \right|dx}=\int\limits_{0}^{1}{\left[ -\left( x-1 \right) \right]dx}+\int\limits_{1}^{2}{\left( x-1 \right)dx}Obie te całki to proste, zwykłe, całki oznaczone, licząc je tak, jak się powinno, otrzymam:
\int\limits_{0}^{2}{\left| x-1 \right|dx}=\int\limits_{0}^{1}{\left| x-1 \right|dx}+\int\limits_{1}^{2}{\left| x-1 \right|dx}=\int\limits_{0}^{1}{\left[ -\left( x-1 \right) \right]dx}+\int\limits_{1}^{2}{\left( x-1 \right)dx}=\frac{1}{2}+\frac{1}{2}=1Krok 3
Odpowiedź to właśnie ta policzona całka wyżej 🙂
Przykład 3
Do policzenia jest całka: \int\limits_{-2}^{-1}{\left| -{{x}^{2}}+3x-2 \right|dx}
Krok 1
Określasz, gdzie -{{x}^{2}}+3x-2\ge 0, a gdzie -{{x}^{2}}+3x-2<0. Tym razem nie będzie tak z górki, bo są to nierówności kwadratowe. Czyli już szkoła średnia, delty, te sprawy.
-{{x}^{2}}+3x-2\ge 0 \Delta ={{3}^{2}}-4\cdot \left( -1 \right)\cdot \left( -2 \right)=1 {{x}_{1}}=\frac{-3-\sqrt{1}}{2\cdot \left( -1 \right)}=\frac{-4}{-2}=2 {{x}_{2}}=\frac{-3+\sqrt{1}}{2\cdot \left( -1 \right)}=\frac{-2}{-2}=1Szkicuję przybliżony wykres funkcji kwadratowej (zgodnie zasadami ze szkoły średniej):

Z wykresu odczytuję, że -{{x}^{2}}+3x-2\ge 0 dla x\in \left\langle 1,2 \right\rangle , a -{{x}^{2}}+3x-2<0 dla x\in \left( -\infty ,1 \right)\cup ( 2,\infty ).
Krok 2
Całka, którą masz policzyć jest liczona dla x-sów od -2 do -1. Zgodnie z Krokiem 1 w tym przedziale pod wartością bezwzględną są tylko argumenty ujemne. Nie ma więc potrzeby rozbijania całki na dwie, albo liczenia jakiś przypadków. Po prostu akurat tutaj:
\int\limits_{-2}^{-1}{\left| -{{x}^{2}}+3x-2 \right|dx}=\int\limits_{-2}^{-1}{\left[ -\left( -{{x}^{2}}+3x-2 \right) \right]dx}=8\tfrac{5}{6}
Krok 3
Już jest 🙂
Przykład 3
Policzyć całkę: \int\limits_{\tfrac{1}{2}}^{e}{\left| \ln x \right|dx}.
Krok 1
Sprawdzamy, gdzie \ln x\ge 0, a gdzie \ln x<0.
Nierówność \ln x\ge 0 można „rozwiązać”, szkicując po prostu wykres funkcji \ln x, albo „mykiem” jak w nierównościach logarytmicznych:
\ln x\ge 0 /{{e}^{( )}}
{{e}^{\ln x}}\ge {{e}^{0}} x\ge 1Analogicznie też, \ln x<0 dla x<1, a pamiętając o dziedzinie logarytmu (może być liczony tylko z liczb dodatnich), dla x\in \left( 0,1 \right).
Wiem zatem, że \ln x\ge 0 dla x\in <1,\infty >, a \ln x<0 dla x\in \left( 0,1 \right).
Krok 2
Moja całka to: \int\limits_{\tfrac{1}{2}}^{e}{\left| \ln x \right|dx} i jest liczona w przedziale od \frac{1}{2} do e. W tym przedziale wyrażenie pod wartością bezwględną \ln x jest raz dodatnie, a raz ujemne. Muszę więc rozbić całkę na dwie:
\int\limits_{\tfrac{1}{2}}^{e}{\left| \ln x \right|dx}=\int\limits_{\tfrac{1}{2}}^{1}{-\ln x}dx+\int\limits_{1}^{e}{\ln x}dxLicząc odpowiednio i osobno obie całki, otrzymuję wynik:
\int\limits_{\tfrac{1}{2}}^{e}{\left| \ln x \right|dx}=\int\limits_{\tfrac{1}{2}}^{1}{-\ln x}dx+\int\limits_{1}^{e}{\ln x}dx=\frac{3}{2}-\frac{\ln 2}{2}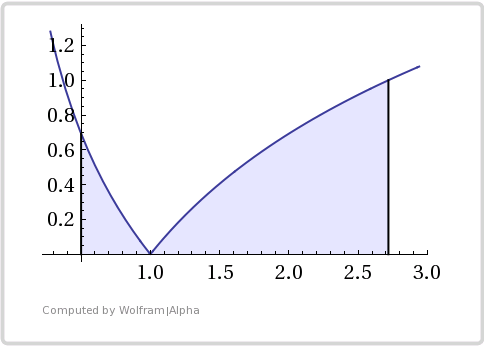
Krok 3
Zrobione 🙂
Zakończenie
To by było chyba na tyle, mam nadzieję, że po przeczytaniu tego posta złapałeś ogólny kierunek, w którym trzeba dążyć mając wartości bezwzględne w całkach, czy innych zadaniach. Najpierw analiza tego, jaki znak przyjmuje argument wartości bezwzględnej, a później umiejętne jej „opuszczenie”, co wiąże się najczęściej z rozbiciem zadania na przypadki.
Dzięki.
Jak zawsze – jeśli masz jakieś pytania, lub przykłady z wartościami bezwzględnymi, wrzucaj je śmiało w komentarzach pod tym postem.
A przy okazji – internetowy kalkulator Wolfram|Alpha radzi sobie świetnie także z całkami z wartościami bezwzględnymi, w sekundę podając gotowy wynik. Wpisywanie do niego całek jest również bardzo proste. Jeśli chcesz, zobacz jak z niego skorzystać w moim darmowym Poradniku do WolframAlpha.


7 Komentarzy
Adam
Czy stałe całkowania w poszczególnych przedziałach mogą się różnić? Czy np. w dla |x| funkcja pierwotna może mieć postać ?
?
Adam
Czy stałe całkowania w poszczególnych przedziałach mogą się różnić? Czy np. w dla |x| funkcja pierwotna może mieć postać ?
?
Asia
Witam,
Mam pytanie odnośnie przypadku f(x) = ln|x| gdy moduł znajduje się w środku logarytmu naturalnego. Mam za zadanie obliczyć pole obszaru ograniczonego krzywymi y=ln|x| y=0 x=-e^2 oraz x=-e i wykres zrobiłam wszystko ładnie, pięknie i mam całkę oznaczoną od -e^2 do -e z ln|x|dx i na prawdę nie mam pojęcia jak to rozbić, na jakie całki, że ln(-x) i lnx? i w jakim przedziale, bo nie mam pomysłu co może być między -e^2 a -e. Byłabym wdzięczna za jakiekolwiek rozjaśnienie mi takiego przypadku jeśli to nie problem 🙂
Pozdrawiam serdecznie
Asia
Już mnie olśniło 🙂 Zamiast pomyśleć dwa razy to zawsze dopatruję się trudności w czymś banalnie prostym (ale chyba zazwyczaj tak jest, że to co najprostsze sprawia największą trudność a nie powinno 🙂 ). Bo ln(x) zawsze jest dodatni więc w całce oznaczonej wstawiając -e czy -e^2 będzie ln(e) i ln(e^2) 🙂 i wszystko ładnie wychodzi tak jak powinno. Także przepraszam i pozdrawiam :).
kanapka94
Jasno, klarownie, pięknie! 🙂
Patrycja
skąd wiadomo jak rozbić przedziały całek? w Przykładzie 2 było (0,2) a rozbiliśmy to na (0,1) i (1,2)
Krystian Karczyński
Wyznaczyłem to w kroku 1 tego przykładu.