Przedstawiam kolejny z serii kalkulatorów, tym razem do równań różniczkowych (a propos nowo powstającego Kursu):
Jak używać kalkulatora?
Kalkulator jest gotowy do obliczeń, trzeba tylko wpisać do niego równanie (zgodnie z ogólną instrukcją wpisywania formuł matematycznych), kliknąc na 'Oblicz’ i mamy rozwiązanie. Jako pochodną funkcji y mozna wpisywać zarówno: y’, jak i: dy/dx .
Kalukatorek ma swoje ograniczenia, to znaczy na pewno nie rozwiąże każdego możliwego równania i bardzo uparcie (za bardzo) wyznacza rozwiązanie w postaci rozwikłanej (co to jest postać uwikłana i rozwikłana rozwiązania równania różniczkowego możesz dowiedzieć się z mojego Kursu Równań Różniczkowych, który powinien ukazać się już w przyszłym tygodniu).
Nie widać też toku rozwiązywania równania, ale i tak przyda się każdemu, kto chce sprawdzić wynik, albo po prostu szybko coś policzyć, co jest potrzebne do czegoś innego.
Z tymi wynikami też trzeba uważać, bo jak wiemy w równaniach różniczkowych na przykład: 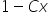 i
i 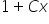 to jedno i te same rozwiązanie równania różniczkowego (dlaczego? – zapraszam znowu do mojego Kursu). Bez paniki więc, jeśli to co mamy na kartce różni się z pozoru od tego, co nam wyszło w kalkulatorze. Ta sama uwaga zresztą tyczy się sprawdzania z odpowiedziami np. w książce.
to jedno i te same rozwiązanie równania różniczkowego (dlaczego? – zapraszam znowu do mojego Kursu). Bez paniki więc, jeśli to co mamy na kartce różni się z pozoru od tego, co nam wyszło w kalkulatorze. Ta sama uwaga zresztą tyczy się sprawdzania z odpowiedziami np. w książce.
Jeśli macie jakieś pytania odnośnie kalkulatora, nie wiecie, jak wpisać do niego jakieś równanie – wrzucajcie je śmiało w komentarzach 🙂


88 Komentarzy
Dzień dobry dostałem taką zagadkę
1+1=1
Czy mógłby mi ktoś pomóc z rozwiązaniem?
Rozwiąż równanie różniczkowe Riccatiego y’=y^2-xy-x wiedzac, że y=ax+b jest rozwiązaniem szczególnym.
Iga
Mam problem z poniższym przykładem, mogłabym prosić o pomoc z rozwiązaniem?
Rozwiąż zagadnienie Cauchy’ego: y’=(1-y^2)x, y(0)=3
Anna
Mogę prosić o pomoc przy rozwiązaniu przykładu:
y’=(cos2x – sin2x) y^3
1. x^2 * (dy/dx) + y – 1 =0 (rozwiązać równanie różniczkowe o zmiennych rozdzielonych)
2. y’ = (y/x) + 1 (rozwiązać równanie różniczkowe)
Bardzo prosiłbym o rozwiązanie tych przykładów z chociaż najprostszym wyjaśnieniem …. niestety nie zrozumiałem ich na wykładzie i teraz nie umiem nic ruszyć żadnego z nich :/
Energetyk98
Na studiach inżynierskich udało mi się przy pomocy Pana kursów E trapez zaliczyć matematykę na wysokie oceny. Teraz po kilku latach przerwy od matematycznych przedmiotów sporo zapomniałem i mam problem z zadaniem na studiach magisterskich. Uprzejmie proszę o pomoc w poniższym zadaniu.
Równanie różniczkowe zwyczajne pierwszego rzędu.
Korzystając z metody Eulera, wyznaczyć przybliżone rozwiązanie y'(t) następującego problemu wartości początkowej:
dy/dt=2(y-1); y(0)=3; t należy [0,2]
dla kroków czasowych: h=1/2; h=1/4; h=1/8; h=1/16; h=1/32
Następnie proszę rozwiązać powyższe równanie różniczkowe metodą zmiennych rozdzielonych.
Monia
Rozwiąż równanie różniczkowe II rzędu:
y”=1-(y’)^2
Krystian
Sposób rozwiązywania tego typu równań (drugiego rzędu sprowadzalne do pierwszego przez podstawienie) przedstawiłem w tej Lekcji.
Pójdzie tak:
Stosuję teraz podstawienie:
I dalej już ciurkiem metodą zmiennych rozdzielonych:
Wracamy teraz do podstawienia:
No i rozwiązujemy tą całeczkę:
Jest to całka wymierna:
Krenig Kacper 1PBA 19
y=−3(x+2)2−4
prosze o odpowiedź
Krystian
A jakie jest pytanie?
Magda
mogę prosic o rozwiązanie?
Zadanie. Rozwiązać rownanie różniczkowe postaci y’=3×2-y , w przedziale od x=0 do x=2, warunek początkowy y(0)=-1, krok calkowania h=0,5. Użyć polepszoną metodę eulera. narysować wykres obliczonej funkcji.
Agata
Czy mogłby mi ktoś pomóc z rozwiązaniem ?
y’-y=(x^2+ 2x + 1)e^x
Bardzo proszę ! 🙂
Krystian Karczyński
Jasne.
Stosując metodę „uzmienniania stałej”, pokazaną w Lekcji 3 mojego Kursu do równań różniczkowych, jadę tak:
Rozwiązuję najpierw odpowiadające temu równaniu równanie jednorodne:
Mam w ten sposób rozwiązanie równania jednorodnego. W rozwiązaniu tym „uzmienniam stałą” i wiem, że rozwiązanie będzie postaci:
Liczę pochodną z tej postaci:
Wstawiam tą postać i jej pochodną do równania na samym początku, czyli do równania , i mam:
, i mam:
Czyli:
Moje rozwiązanie równania jest więc równe:
Odp.
Zapraszam do mojego Kursu z równań różniczkowych.
GalachadV (Edyta)
Witam! W jakiej postaci należy przewidzieć rozwiązanie równania niejednorodnego różniczkowego: y” – 2y’ +10y = 6e^(x) sin (3x), równanie jednorodne ma rozwiązanie ogólne: y = C(1) e^(x) sin (3x) + C(2) e^(x) cos (3x). Będę wdzięczna za pomoc. Pozdrawiam Edyta (GalachadV)
Krystian Karczyński
Witam!
Zaglądamy do odpowiedniej tabelki i orientujemy się, że prawa strona równania pasuje nam do postaci:
bo:
Zgodnie z tabelką, przewidujemy więc rozwiązanie w postaci:
Nie jest to jednak prawidłowa odpowiedź! Tak jak pokazuję w moim Kursie do równań różniczkowych, trzeba tutaj zorientować się, że…
Co w tej sytuacji robimy?
Ano zwiększamy o 1 stopnie wielomianów w postaci przewidywanej, uzyskując wielomiany pierwszego stopnia, czyli:
I to jest dopiero postać, w której przewidujemy rozwiązanie szczególne równania.
Odp.
Ten i podobne „myki” związane z równaniami różniczkowymi II rzędu pokazuję w mojej Lekcji Video im poświęconej. Cały Kurs tutaj.
Łukasz
Krystian Karczyński
Pierwsza pójdzie tak (metoda przez podstawienie):
Druga przez części:
Trzecia też przez części:
Paweł
a co jeśli mamy równanie i do tego warunki początkowe x0 ,y0=…….
Kasia
Dzień dobry, czy ktoś mógłby mi pomóc z rozwiązaniem równania różniczkowego: (y”)^2 =4y’ Byłabym wdzięczna za pomoc 🙂
eliza
Dzień dobry Potrzebuje pomocy w rozwiązaniu następującego równaniady/dx=x/y* (1+x)/(1+y)
Kasia
Potrzebuję pomocy z równaniem różniczkowym II rzędu: y”- 2y’ +2y = [e^(2x)] +xy=yj + ypPoliczyłam yj= [e^(x)]*(C1cosx + C2sinx)Nie wiem jak policzyć yp, czy ktoś wie jak to rozwiązać?
Kasia
y”- 2y’ +2y = [e^(2x)] +x piszę jeszcze raz, bo pomimo spacji źle się zapisało
Kumori
Dzień dobry! Czy ktoś jest w stanie pomóc mi z analitycznym rozwiązaniem krok po kroku równania:y’ + 3 y = 4 Sin4x, y(0)=1Z góry dziękuję!
Moniaa
Witam. Pomoże ktoś w rozwiązaniu układu dx/dt=y dy/dt=-x metodą różniczkowa?
Berner paulina
pomoze mi ktos rozwiazac zadanie ?x’=pod pierwiastkiem arctg(t) / t^2+1
haniasss
Potrzebuję pomocy z rozwiązaniem następującego zdania:y(3)+y’-10y=10e^x*sin2x
Dawid
y1=(1-y1-y2)y1 y’2=(a-y2-4a2y1)y2 a to jak zapisać ?
Dawid
dla a=0.1
BBB
W kursie, w lekcji drugiej jest błąd, w przykładzie , w momencie
, w momencie  za „t” podstawiasz
za „t” podstawiasz  a przecież mamy podstawić „t” a nie „1”, dzięki temu rozwinięcie przykładu wygląda zupełnie inaczej, wynik pewnie też. Pozdrawiam. Prosiłbym o ewentualne rozwinięcie prawidłowego przykładu.
a przecież mamy podstawić „t” a nie „1”, dzięki temu rozwinięcie przykładu wygląda zupełnie inaczej, wynik pewnie też. Pozdrawiam. Prosiłbym o ewentualne rozwinięcie prawidłowego przykładu.
Ania
Witam. Czy mógłby mi ktoś pomóc z równaniem : x^2*y’=sin(1/x)? 🙁
Krystian Karczyński
To będzie równanie o zmiennych rozdzielonych. Pójdzie to tak (polecam tutaj mój Kurs, gdzie pokazuję, jak to się robi):
…
Całkę po prawej stronie rozwiązujemy „na boczku” przez podstawienie:
Wracając więc do równania mamy:
…
I rozwiązane.
Maciej1
Witam, mam problem z rozwiązaniem równania (2xy^2-y)dx+(y^2+x+y)=0.
Krzysiek22
Witam, mam problem z rozwiązaniem równania y’+ty=t za pomocą czynnika całkującego. Przez uzmiennianie stałej wychodzi mi dobry wynik y=1+Ce^(-0,5t^2).Z góry dziękuję
andtom
Mam jeszcze problem z następujacym zadaniem:( x^2+2xy-y^2)dx+(y^2+2xy-x^2)dy=0Nie jest ono zupełne bo różniczki nie są takie same, nie są też postaci f(y/x)O ile to możliwe, to prosiłbym o pomoc.Z góry dziękujęAndtom
andtom
Czy mógłbym prosić o rozwiązanie równania różniczkowego xdx+(y+1)dy=0Wartości y otrzymuje w postaci uwikłanej, czy jest jakiś sposób na rozwikłanie tego.
Joanna Grochowska
Jest to równanie liniowe o zmiennych rozdzielonych. Porządkuję więc je tak, by po jednej stronie mieć wyrażenia związane z „y”, a po drugiej z „x”.
Mam więc rozwiązane równanie, ale w postaci uwikłanej (tzn. nie mam wprost wyliczonego „y=….”, ale jakieś wyrażenie z „y”).
Alby je „rozwikłać”, czyli wyliczyć samego „y”, musimy popatrzeć jakie mamy to wyrażenie/równanie z igrekami. Jak widać jest to równanie kwadratowe, z tym że inaczej niż pamiętamy ze szkoły średniej (bo nie na „x”, ale na „y” – to jest moja zmienna). Dla pełnej jasności przeniosę wszystko na jedną stronę
Stąd mam że:
Liczę deltę:
Stąd moje wartości y, czyli „jawne” rozwiązania:
andtom
Serdeczne dzięki za pomoc. Pozdrawiam.
ewcia5665
ydy/dx=1-xy dx/dy=(1-x)ydy=(1-x)dx y^2=x^2+c i nie nie wiem co dalej
y^2=x^2+c i nie nie wiem co dalej
Joanna Grochowska
Domyślam się, że to to samo równanie zamieszczone wyżej prawda? Wyżej pokazałam jak je rozwiązać 🙂
ewcia5665
ydy/dx=1-x
Joanna Grochowska
Jest to równanie liniowe o zmiennych rozdzielonych, doprowadzam do tego, by po jednej stronie mieć same „y”, po drugie stronie wyrażenia z „x” i pozostałe.
Całkuję obie strony
Ada
3 dy/dx = – [1 + 3y kwadrat] y(0) = 1/3
Nie mogę sobie poradzić z tą całką. Proszę o pomoc.
Paulina
Witam można prosić o pomoc? Ogólnie mam takie równanie: i z tego potrzebuję :
i z tego potrzebuję :  ,
,  ,
,  ,
,  . Niby wiem na jakiej zasadzie to działa, ale nie mam pojęcia jak to rozpisać. Byłabym bardzo wdzięczna za pomoc i ewentualne wytłumaczenie.
. Niby wiem na jakiej zasadzie to działa, ale nie mam pojęcia jak to rozpisać. Byłabym bardzo wdzięczna za pomoc i ewentualne wytłumaczenie.
Paulina
: , to czy te rozwiązania są poprawne?
, to czy te rozwiązania są poprawne? 

 czy to raczej totalna głupota?
czy to raczej totalna głupota?
Mateusz
y(x) = x (y'(x) – y”(x)) bardzo proszę o pomoc z tym rownaniem.
Martyna
Jak potraktować takie równanie:d^(2)x/dt^2 + x =0potrzebuję tylko początkowego wyjścia.Nie jestem pewna czy mogę zapisać to w takiej postaci: x” +x =0
Anna Zalewska
Faktycznie, można to równanie zapisać w postaci: , gdzie
, gdzie  .
.
Mamy tu do czynienia z równaniem różniczkowym drugiego rzędu linowym jednorodnym o stałych współczynnikach.
Dla takiego równania przewidujemy rozwiązanie szczególne w postaci funkcji wykładniczej: .
. .
.
Mamy więc:
Podstawiamy do podanego równania i otrzymujemy:
Ponieważ w tym równaniu mamy , postąpimy według następującego schematu:
, postąpimy według następującego schematu:
całki szczególne:
całka ogólna:
Dla naszego przykładu:
całki szczególne:
całka ogólna:
Syll
x*dy/dx-y = 2x^3
pilnie proszę o pomoc..
Kamil Kocot
Witam
To jest zwykłe równanie liniowe, rozwiążę je metodą uzmienniania stałej.
1) równanie jednorodne
Przejście w ostatniej linijce jest standardowe, należy zapamiętać bo to wynika z definicji logarytmu, własności logarytmu
oraz własności potęgowania. Wyjaśnienie jest następujące
gdzie przyjmujemy w skrócie, że .
.
Powracając do przykładu, w punkcie
2) uzmienniamy stałą tzn.
3) Obliczamy pochodną
4) Wstawiamy do początkowego równania (zarówno y jak i y’) tzn.
Wyliczone C(x) wstawiamy do punktu 2) i dostajemy rozwiązanie
Piter
Proszę o pomoc u”+u=cos2x
Syll
xdy/dx-y = 2x^3
pilnie proszę o pomoc..
Kamil Kocot
Równanie jest równaniem różniczkowym rzędu II-ego. Rozwiążemy je w dwóch etapach, najpierw równanie jednorodne a później równanie niejednorodne metodą przewidywań. Wszystko zostało omówione też w lekcji Pana Krystiana
jest równaniem różniczkowym rzędu II-ego. Rozwiążemy je w dwóch etapach, najpierw równanie jednorodne a później równanie niejednorodne metodą przewidywań. Wszystko zostało omówione też w lekcji Pana Krystiana
https://online.etrapez.pl/lesson/lekcja-5-rownania-rozniczkowe-ii-rzedu-liniowe-o-stalych-wspolczynnikach-sprowadzalne-do-rownan-i-go-rzedu/
Zatem
1) Etap I (za prawą stronę podstawiamy zero, rozwiązujemy równanie charakterystyczne)
Ponieważ rozwiązanie wychodzi zespolone stąd rozwiązaniem równania jednorodnego jest zgodnie ze schematem
stąd rozwiązaniem równania jednorodnego jest zgodnie ze schematem  czyli
czyli
2) Etap II
Przewidujemy rozwiązanie równania niejednorodnego na podstawie funkcji znajdującej się po prawej stronie tj.
na podstawie funkcji znajdującej się po prawej stronie tj.  . Przewidujemy je jako
. Przewidujemy je jako
Podane nie zawiera się w rozwiązaniu równania jednorodnego (mamy w nim
nie zawiera się w rozwiązaniu równania jednorodnego (mamy w nim  a tu jest cos2x ), tym samym jest to dobre rozwiązanie. W dalszym etapie wyliczamy
a tu jest cos2x ), tym samym jest to dobre rozwiązanie. W dalszym etapie wyliczamy  i podstawiamy do początkowego równania.
i podstawiamy do początkowego równania.
Porównując współczynniki przy po lewej i prawej stronie dostajemy
po lewej i prawej stronie dostajemy
czyli
Odp.:
ROck
Kto pomoże ? y’-(y +cosx)sinx=0
Kamil Kocot
Mamy tu do czynienia z równaniem liniowym I-go rzędu. Rozwiązujemy w dwóch etapach 1) równanie jednorodne i 2) równanie niejednorodne metodą uzmienniania stałej.
1) Równanie jednorodne
2) Uzmiennianie stałej
Wstawiamy do równania i dostajemy
i dostajemy
Wyliczamy całkę na boku
czyli oraz ostateczna odpowiedź po wstawieniu do 2) za C(x):
oraz ostateczna odpowiedź po wstawieniu do 2) za C(x):
Kamil
Bardzo proszę o pomoc w rozwiązaniu równania:
y’=y+y/x+x
Kamil Kocot
Mamy tutaj równanie liniowe, które można zapisać w postaci
1) Rozwiązujemy równanie jednorodne
2) Uzmienniamy stałą
i obliczamy pochodną jako iloczyn 3 funkcji
Wstawiając do równania początkowego dostajemy
dostajemy
Następnie powracając do 2) i wstawiając w miejsce C(x) otrzymujemy rozwiązani
Karolina
A równań różniczkowych II rzędu nie liczy?
JOANNA
proszę o rozwiązanie równania u”-u’-y=0 lub p’-p-y=0. Bardzo proszę o pomoc.
studentka
Bardzo proszę o rozwiązanie tego równania różniczkowego próbowałam wiele razy i wychodzą mi jakieś głupoty. Bardzo proszę o pomoc : 2y’lnt+y/t=(1/y)(cost)^2
Kamil Kocot
Równanie
jest równaniem różniczkowym Bernoulliego tzn. równaniem typu
Rozwiążemy je zgodnie ze schematem podanym w kursie Pana Krystiana
https://online.etrapez.pl/lesson/lekcja-4-niektore-rownania-nieliniowe-rzedu-pierwszego-rownanie-rozniczkowe-rodziny-linii/
Z postaci równania wynika, że . Robimy podstawienie
. Robimy podstawienie  czyli
czyli  . Następnie obliczamy pochodną pamiętając o tym, że y jest funkcją zmiennej t, zatem pochodną
. Następnie obliczamy pochodną pamiętając o tym, że y jest funkcją zmiennej t, zatem pochodną  wyliczamy jako pochodną złożoną tzn.
wyliczamy jako pochodną złożoną tzn.
Wracamy do równania, troszeczkę przekształcamy i podstawiamy to co powyżej
Powyższe równanie jest równaniem liniowym, rozwiązujemy je metodą uzmienniania stałej
1) Równanie jednorodne
2) Uzmiennianie stałej
Wstawiamy do i dostajemy
i dostajemy
Po wstawieniu do 2) mamy
Na sam koniec powracamy z podstawieniem czyli
czyli
Uwaga! Program Wolfram zwraca troszkę inny wynik ale jest on równoważny powyższemu.
Joanna
Witam mam problem z równaniem różniczkowym dy/dx- (2yx)/(x^2 + 4)= 1/(x+2) bardzo proszę o pomoc byłabym bardzo wdzięczna 🙂
Krystian Karczyński
Witam, to zwykłe liniowe, z tym, że trochę się przedłuży, bo wyjdzie po drodze całka wymierna. Lecę metodami z mojego Kursu Równań Różniczkowych:
frac{dy}{dx}-frac{2x}{{{x}^{2}}+4}y=frac{1}{x+2}
frac{dy}{dx}-frac{2x}{{{x}^{2}}+4}y=0
frac{dy}{dx}=frac{2x}{{{x}^{2}}+4}yquad /:y/cdot dx
frac{dy}{y}=frac{2x}{{{x}^{2}}+4}dxquad /int{{}}
int{frac{dy}{y}}=int{frac{2x}{{{x}^{2}}+4}dx}
ln left| y right|=ln left| {{x}^{2}}+4 right|+Cquad /{{e}^{left( ldots right)}}
{{e}^{ln left| y right|}}={{e}^{ln left| {{x}^{2}}+4 right|+C}}
left| y right|={{e}^{ln left| {{x}^{2}}+4 right|}}{{e}^{C}}
y=Cleft( {{x}^{2}}+4 right)
y=Cleft( x right)left( {{x}^{2}}+4 right)
{y}'={C}'left( x right)left( {{x}^{2}}+4 right)+Cleft( x right)2x
{C}'left( x right)left( {{x}^{2}}+4 right)+Cleft( x right)2x-frac{2x}{{{x}^{2}}+4}Cleft( x right)left( {{x}^{2}}+4 right)=frac{1}{x+2}
{C}'left( x right)left( {{x}^{2}}+4 right)=frac{1}{x+2}quad /:left( {{x}^{2}}+4 right)
{C}'left( x right)=frac{1}{left( x+2 right)left( {{x}^{2}}+4 right)}quad /int{{}}
Cleft( x right)=int{frac{1}{left( x+2 right)left( {{x}^{2}}+4 right)}dx}
No i to jest właśnie ta wymierna do rozwalenia. Prosta, ale żmudna. Pokazuję cały schemat na tej Lekcji, a tutaj tylko stosuję:
int{frac{1}{left( x+2 right)left( {{x}^{2}}+4 right)}dx}
frac{1}{left( x+2 right)left( {{x}^{2}}+4 right)}=frac{A}{x+2}+frac{Bx+C}{{{x}^{2}}+4}quad /cdot left( x+2 right)left( {{x}^{2}}+4 right)
1=Aleft( {{x}^{2}}+4 right)+left( Bx+C right)left( x+2 right)
1=A{{x}^{2}}+4A+B{{x}^{2}}+2Bx+Cx+2C
{ begin{matrix}
& 0=A+Bquad Rightarrow A=-B \
& 0=2B+C \
& 1=4A+2C end{matrix}
{ begin{matrix}
& 0=2B+Cquad Rightarrow C=-2B \
& 1=-4B+2C end{matrix}
1=-4B-4B
B=-frac{1}{8}
C=frac{1}{4},A=frac{1}{8}
Wracam się do całki:
int{frac{1}{left( x+2 right)left( {{x}^{2}}+4 right)}dx}=int{frac{tfrac{1}{8}}{x+2}dx}+int{frac{-tfrac{1}{8}x+tfrac{1}{4}}{{{x}^{2}}+4}dx}=
=frac{1}{8}int{frac{1}{x+2}dx}-frac{1}{8}int{frac{x}{{{x}^{2}}+4}dx+frac{1}{4}int{frac{1}{{{x}^{2}}+4}dx}}=
Tu trochę przyspieszę, bo wszystkie trzy całki są proste:
=frac{1}{8}ln left| x+2 right|-frac{1}{16}ln left| {{x}^{2}}+4 right|+frac{1}{8}arctgfrac{x}{2}+C
Mając rozwiązaną całkę, wracam się do równania:
Cleft( x right)=frac{1}{8}ln left| x+2 right|-frac{1}{16}ln left| {{x}^{2}}+4 right|+frac{1}{8}arctgfrac{x}{2}+C
Czyli jeszcze jeden „powrót” i mam rozwiązanie:
y=left( frac{1}{8}ln left| x+2 right|-frac{1}{16}ln left| {{x}^{2}}+4 right|+frac{1}{8}arctgfrac{x}{2}+C right)left( {{x}^{2}}+4 right)
Joanna
Dziękuje za pomoc 🙂
Paweł
Witam, dziękuję za kalkulator, super sprawa 🙂 Aczkolwiek chyba to dla mnie niewystarczające, bo nie potrafię dojść do tego czemu nie wychodzi mi takie rozwiązanie jak powinno. Jakbym mógł prosić o pomoc w rozwiązaniu równania różniczkowego to byłbym bardzo wdzięczny 🙂 Równanie: x * y’ = y * ln (x/y)
Krystian Karczyński
Witam. To równanie jednorodne względem y i x, polecam odpowiednią Lekcję z mojego Kursu Równań Różniczkowych, na której omawiam wszystkie potrzebne patenty i przejścia.
x{y}'=yln left( frac{x}{y} right)
x{y}'=yln left( frac{x}{y} right)quad /:x
{y}'=frac{y}{x}ln left( frac{1}{tfrac{y}{x}} right)quad /:x
Teraz odpowiednie podstawienie:
t=frac{y}{x}
y=tx
{y}'={{left( tx right)}^{prime }}={t}'x+t
{t}'x+t=tln left( frac{1}{t} right)
frac{dt}{dx}x=tln left( frac{1}{t} right)-tquad /cdot dx/:x
dt=tleft( ln left( frac{1}{t} right)-1 right)frac{dx}{x}quad /:tleft( ln left( frac{1}{t} right)-1 right)
frac{dt}{tleft( ln left( tfrac{1}{t} right)-1 right)}=frac{dx}{x}quad /int{{}}
int{frac{dt}{tleft( ln left( tfrac{1}{t} right)-1 right)}}=int{frac{dx}{x}}
Na boku liczę całkę int{frac{dt}{tleft( ln left( tfrac{1}{t} right)-1 right)}}
int{frac{dt}{tleft( ln left( tfrac{1}{t} right)-1 right)}}=int{frac{dt}{tleft( ln left( {{t}^{-1}} right)-1 right)}}=int{frac{dt}{tleft( -ln t-1 right)}}=left| begin{matrix}
& u=-ln t-1 \
& du=-frac{1}{t}dt \
& -du=frac{dt}{t} end{matrix} right|=int{frac{-du}{u}}=-ln left| u right|+C=
=-ln left| -ln t-1 right|+C
Wracam się z wynikiem do równania różniczkowego:
-ln left| -ln t-1 right|=ln left| x right|+C
ln left| -ln t-1 right|=-ln left| x right|+C
ln left| -ln t-1 right|=ln {{left| x right|}^{-1}}+Cquad /{{e}^{left( ldots right)}}
{{e}^{ln left| -ln t-1 right|}}={{e}^{ln {{left| x right|}^{-1}}}}{{e}^{C}}
-ln t-1=frac{C}{x}
-ln t=frac{C}{x}+1
ln t=frac{C}{x}-1quad /{{e}^{left( ldots right)}}
t={{e}^{tfrac{C}{x}-1}}
frac{y}{x}={{e}^{tfrac{C}{x}-1}}quad /cdot x
y=x{{e}^{tfrac{C}{x}-1}}– i to jest wynik 🙂
Paweł
Bardzo dziękuję, jestem niezmiernie wdzięczny 🙂 A z Pana lekcji na pewno skorzystam 🙂
Aleksandra
A to jak by Pan rozwiązał :y’-2/x*y=4x^3 ? Mam potem problem ze ”skreśleniem”.
Krystian Karczyński
Nie wiem, czy dobrze odczytałem, lecę metodami z mojego Kursu Video do równań różniczkowych:
{y}'-\frac{2}{x}y=4{{x}^{3}}
{y}'-\frac{2}{x}y=0
\frac{dy}{dx}=\frac{2y}{x}
\frac{dy}{y}=\frac{2dx}{x}\quad /\int{\left( \ldots \right)}
\int{\frac{dy}{y}}=\int{\frac{2dx}{x}}
ln \left| y \right|=2ln \left| x \right|+C
ln \left| y \right|=ln {{\left| x \right|}^{2}}+C\quad /{{e}^{\left( \ldots \right)}}
{{e}^{ln \left| y \right|}}={{e}^{ln {{\left| x \right|}^{2}}+C}}
{{e}^{ln \left| y \right|}}={{e}^{ln {{\left| x \right|}^{2}}}}{{e}^{C}}
y=C{{x}^{2}}
y=C\left( x \right){{x}^{2}}
{y}'={C}'\left( x \right){{x}^{2}}+C\left( x \right)\cdot 2x
Podstawiając do wyjściowego równania:
{C}'\left( x \right){{x}^{2}}+C\left( x \right)\cdot 2x-\frac{2}{x}C\left( x \right){{x}^{2}}=4{{x}^{3}}
{C}'\left( x \right){{x}^{2}}+2xC\left( x \right)-2xC\left( x \right)=4{{x}^{3}}
{C}'\left( x \right){{x}^{2}}=4{{x}^{3}}\quad /:{{x}^{2}}
{C}'\left( x \right)=4x\quad /\int{\left( \ldots \right)}
C\left( x \right)=\int{4x}dx=2{{x}^{2}}+C
I mam rozwiązanie:
y=\left( 2{{x}^{2}}+C \right){{x}^{2}}=2{{x}^{4}}+C{{x}^{2}}
Monika
Witam, mam problem z różniczka: dy/dx+y/x=2 proszę o pomoc
Krystian Karczyński
Po pierwsze: to jest „równanie różniczkowe”, a nie: „różniczka” 🙂
A po drugie…
\frac{dy}{dx}+\frac{y}{x}=2
Równanie jest także liniowe, ale rozwiążę je jako jednorodne względem y i x:
Podstawiam:
t=\frac{y}{x}
y=tx
{y}'={{\left( tx \right)}^{\prime }}={t}'x+t{x}'={t}'x+t
Wracam się do równania z tymi podstawieniami:
{t}'x+t+t=2
\frac{dt}{dx}x+2t=2
\frac{dt}{dx}x=2-2t\quad /:x/\cdot dx/\left( 2-2t \right)
\frac{dt}{2-2t}=\frac{dx}{x}\quad /\int{{}}
\int{\frac{dt}{2-2t}}=\int{\frac{dx}{x}}
Całkę po lewej stronie liczę na boku:
\int{\frac{dt}{2-2t}}=\left| \begin{matrix}
& u=2-2t \\
& du=-2dt \\
& dt=\frac{du}{-2} \end{matrix} \right|=-\frac{1}{2}ln \left| u \right|+C=-\frac{1}{2}ln \left| 2-2t \right|+C
-\frac{1}{2}ln \left| 2-2t \right|=ln \left| x \right|+C\quad /\cdot \left( -2 \right)
ln \left| 2-2t \right|=-2ln \left| x \right|+C\quad /{{e}^{\left( \ldots \right)}}
{{e}^{ln \left| 2-2t \right|}}={{e}^{-2ln \left| x \right|+C}}
{{e}^{ln \left| 2-2t \right|}}={{e}^{ln {{\left| x \right|}^{-2}}}}\cdot {{e}^{C}}
2-2t=C\cdot \frac{1}{{{x}^{2}}}
-2\cdot \frac{y}{x}=C\cdot \frac{1}{{{x}^{2}}}-2\quad /\cdot x/:\left( -2 \right)
y=\frac{C}{x}+x
RN
Witam mam problem z równaniem y’=y(2(x^3)-1) y=(2)=1
a mianowicie przy liczeniu rozwiązania szczególnego.
Krystian Karczyński
Zakładam, że warunek początkowy był taki: y(2)=1
Jedziemy 🙂
{y}'=y\left( 2{{x}^{3}}-1 \right)
\frac{dy}{dx}=y\left( 2{{x}^{3}}-1 \right)\quad /:y/\cdot dx
\frac{dy}{y}=\left( 2{{x}^{3}}-1 \right)dx\quad /\int{{}}
\int{\frac{dy}{y}}=\int{\left( 2{{x}^{3}}-1 \right)dx}
\int{\left( 2{{x}^{3}}-1 \right)dx}=\int{2{{x}^{3}}dx}-\int{dx}=2\int{{{x}^{3}}dx}-x+C=2\cdot \frac{1}{4}{{x}^{4}}-x+C=\frac{1}{2}{{x}^{4}}-x+C
ln \left| y \right|=\frac{1}{2}{{x}^{4}}-x+C\quad /{{e}^{\left( \ldots \right)}}
{{e}^{ln \left| y \right|}}={{e}^{\frac{1}{2}{{x}^{4}}-x+C}}
y={{e}^{\frac{1}{2}{{x}^{4}}-x}}\cdot {{e}^{C}}
y=C{{e}^{\frac{1}{2}{{x}^{4}}-x}}
Teraz uwzględniamy warunek początkowy:
1=C{{e}^{\frac{1}{2}\cdot {{2}^{4}}-2}}
1=C{{e}^{6}}\quad /:{{e}^{6}}
C=\frac{1}{{{e}^{6}}}
Zatem nasza odpowiedź to:
{{y}_{sz}}=\frac{1}{{{e}^{6}}}\cdot {{e}^{\frac{1}{2}{{x}^{4}}-x}}=\frac{{{e}^{\frac{1}{2}{{x}^{4}}-x}}}{{{e}^{6}}}={{e}^{\frac{1}{2}{{x}^{4}}-x-6}}
KM
Dlaczego wynik w kalkulatorze y”-2y’ = x nie zgadza sie z wynikiem z kursu
Krystian Karczyński
A gdzie w Kursie jest taki przykład?
Ryhor Abramovich
Rozwiązanie:
To jest równanie różniczkowe II rzędu, nie zawierające niewiadomej funkcji (y). Dlatego możemy obniżyć rząd tego równania za pomocy podstawy.
Niech . Wtedy
. Wtedy  , i równanie zapiszemy w postaci:
, i równanie zapiszemy w postaci:
To jest równanie I rzędu (liniowe). Rozwiązujemy go na 2 sposoby.
Sposob 1 (wg schematu z lekcji 3):
Mamy więc postać rozwiązania równania jednorodnego. „Uzmienniamy” stałą:
Podstawiamy wyniki do równania :
:
Całkę liczymy przez części:
Tak wyliczoną stałą wstawiam do równania z „uzmiennioną” stałą:
Dalej, , czyli
, czyli
Sposób 2.
Podstawa: , czyli
, czyli  . Wtedy
. Wtedy
Wyznaczymy funkcję w taki sposób, żeby wyraz w nawiasie był równym zera:
w taki sposób, żeby wyraz w nawiasie był równym zera:
Uwaga! Do prawej czężci tego równania stałą C nie dodajemy. Dalej:
Podstawiamy do równania, w ktorym były nawiasy:
Skorzystamy z wyników, otrzymanych podczas obliczeń w sposób 1:
Stąd
i, odpowiednio,
Adam Kołodziejski
Prosiłbym o pomoc w rozwiązaniu tego równania
((3/2)*(y^2)*cos(x)+2)*dx= -(3y*sin(x)+1)*dy
Agatha
Witam czy mógłby Pan rozwiązać równanie
x \frac{dy}{dx} + y \frac{dy}{dy} + z^2 y \frac{dy}{dz} = 0
Kurs równań różniczkowych nie bardzo i tu pomógł.
Amelia
Jak jest Pan takim kozakiem to dlaczego po przerobieniu całego kursu z równań różniczkowych nikt z mojego roku nie zdał kolokwium. O chyba robi Pan trywialne przykłady, które mój wykładowca pomija bo są zbyt oczywiste.
Chcecie fun?! Rozwiążcie to:
\frac{x^2}{y^2 + yx} \frac{du}{dx} + {du}{dy} + (1+z^2) \frac{du}{dz} = 0
Krystian Karczyński
To jest przykład z równań różniczkowych cząstkowych, mój Kurs jest do równań różniczkowych zwyczajnych. Sorry, że nie zdaliście kolokwium.
Amelia
Więc może już nadszedł czas, aby stworzyć kolejny kurs.
Mariusz
Czy mógłby Pan rozwiązać poniższe równanie?
xy’=x+3y, y(1)=2
Pozdrawiam serdecznie!
Krystian Karczyński
Dobra, krok po kroku:
x{y}'=x+3y,\quad y\left( 1 \right)=2
x{y}'-3y=x
Czyli to jest zwykłe, liniowe równanie I rzędu. Ruszam ze schematem z mojego Kursu Równań Różniczkowych.
x{y}'-3y=0
x{y}'=3y
x\frac{dy}{dx}=3y\quad /:x \cdot dx :y
\frac{dy}{y}=\frac{3}{x}dx\quad /\int{{}}
\int{\frac{dy}{y}}=\int{\frac{3}{x}dx}\quad /\int{{}}
ln \left| y \right|=3ln \left| x \right|+C
ln \left| y \right|=ln {{\left| x \right|}^{3}}+C\quad /{{e}^{\left( \ldots \right)}}
{{e}^{ln \left| y \right|}}={{e}^{ln {{\left| x \right|}^{3}}+C}}
\left| y \right|={{e}^{ln {{\left| x \right|}^{3}}}}{{e}^{C}}
y=C{{x}^{3}}
„Uzmienniam” stałą:
y=C\left( x \right){{x}^{3}}
{y}'={C}'\left( x \right){{x}^{3}}+C\left( x \right)\cdot 3{{x}^{2}}
x\left( {C}'\left( x \right){{x}^{3}}+C\left( x \right)\cdot 3{{x}^{2}} \right)-3C\left( x \right){{x}^{3}}=x
{C}'\left( x \right){{x}^{4}}+3C\left( x \right){{x}^{3}}-3C\left( x \right){{x}^{3}}=x
{C}'\left( x \right){{x}^{4}}=x\quad /:{{x}^{4}}
{C}'\left( x \right)=\frac{1}{{{x}^{3}}}\quad /\int{{}}
C\left( x \right)=\int{\frac{1}{{{x}^{3}}}dx}=\int{{{x}^{-3}}dx}=\frac{1}{-3+1}{{x}^{-3+1}}+C=
=-\frac{1}{2}{{x}^{-2}}+C=-\frac{1}{2}\frac{1}{{{x}^{2}}}+C=-\frac{1}{2{{x}^{2}}}+C
Czym mam rozwiązanie równania ogólnego:
y=\left( -\frac{1}{2{{x}^{2}}}+C \right){{x}^{3}}=-\frac{x}{2}+C{{x}^{3}}
Teraz uwzględniam warunek początkowy y\left( 1 \right)=2:
2=-\frac{1}{2}+C\cdot {{1}^{3}}
C=2\tfrac{1}{2}
I mogę pisać odpowiedź:
y=-\frac{x}{2}+2\tfrac{1}{2}{{x}^{3}}
Michał
Czy mógłbym prosić o pomoc w rozwiązaniu tego równania: dy/dx-xy^3=-xy ? Dochodzę do momentu gdzie mam już dwie całki i mam problem przy policzeniu całki z dy/y(y^2-1). Można rozłożyć sobie to na trzy ułamki proste, ale nie potrafię potem rozwikłać y.
Ryhor Abramovich
Rozwiązanie:
Zapiszem to równanie w postaci:
To jest równanie Bernoulli’ ego typu
gdzie
Najpierw – podstawa
I liczymy:
Dalej,
To jest równanie liniowe I rzędu. Rozwiązujemy go wg schematu z lekcji 3.
Mamy więc postać rozwiązania równania jednorodnego. „Uzmienniam” stałą:
Wstawiamy wyniki do początkowego równania:
Tak wyliczoną stałą wstawiam do równania z „uzmiennioną” stałą:
Ponieważ , to
, to
Karolina
y”=+4y=4(cos2x+sin2x)
y(pi)=y’ (pi)=2\pi
Krystian Karczyński
Witam, rozumiem, że mam rozwiązać Pani równanie? 🙂
Bo WolframAlpha rozwiązuje je tak:
y”+4y=4(cos2x+sin2x), y(pi)=2pi, y’(pi)=2pi
No, a my poradzilibyśmy sobie tak (lecę metodą przewidywań pokazaną w moim Kursie Video):
Na początku rozwiązujemy równanie jednorodne:
{y}''+4y=0
Równanie charakterystyczne ma więc postać:
{{r}^{2}}+4=0
Delta jest tu ujemna, ale jest ono bardzo proste i możemy sobie poradzić bez delty:
{{r}^{2}}=-4
r=sqrt{-4}
A wiemy, że te pierwiastki istnieją i są zespolone:
r=2i vee r=-2i, bo sqrt{-4}=sqrt{left( -1 right)cdot 4}=sqrt{{{i}^{2}}}cdot sqrt{4}=pm 2i
Czyli korzystając z ogólnego wzoru na rozwiązanie równania jednorodnego (zawarty w Kursie) mam:
{{y}_{j}}={{e}^{0cdot x}}left( Acos 2x+Bsin 2x right)
czyli mam rozwiązanie równania jednorodnego y_j:
{{y}_{j}}=Acos 2x+Bsin 2x
Teraz jedno rozwiązanie szczególne. Zgodnie ze schematem, biorę postać:
{{y}_{p}}=Acos 2x+Bsin 2x
Teraz ważny moment. Zauważam, że to rozwiązanie zawiera się już w rozwiązaniu równania jednorodnego y_j, zatem muszę zwiększyć stopień wielomianów o 1, „przewiduję” więc rozwiązanie w postaci:
{{y}_{p}}=left( Ax+B right)cos 2x+left( Cx+D right)sin 2x
Teraz liczę pochodną i drugą pochodną, porządkując je i pomagając sobie Wolframem:
{{y}_{p}}^{prime }=left( 2Cx+A+2D right)cos 2x+left( -2Ax-2B+C right)sin 2x(obliczenia)
{{y}_{p}}{{^{prime }}^{prime }}=-4left( Ax+B-C right)cos 2x-4left( Cx+A+D right)sin 2x(obliczenia)
Wstawiam drugą pochodną i funkcję do wyjściowego równania i mam:
-4left( Ax+B-C right)cos 2x-4left( Cx+A+D right)sin 2x+4left( left( Ax+B right)cos 2x+left( Cx+D right)sin 2x right)=4left( cos 2x+sin 2x right)
Po ponownym uporządkowaniu Wolframem mam więc:
4Ccos 2x-4Asin 2x=4cos 2x+4sin 2x
Ponieważ stałe Bi Dzredukowały się, mogę przyjąć za nie 0.
Przyrównując więc współczynniki przy cos2xi sin2xmam:
{ begin{matrix}
& 4C=4
& -4A=4 end{matrix} Rightarrow { begin{matrix}
& C=1
& A=-1 end{matrix}
Podstawiając więc wszystko do ogólnego wzoru {{y}_{p}}=left( Ax+B right)cos 2x+left( Cx+D right)sin 2xmam policzone y_p:
{{y}_{p}}=-xcos 2x+xsin 2x
Mając y_ji y_pmogę już wyznaczyć rozwiązanie ogólne równania ze wzoru y=y_j+y_p:
y=Acos 2x+Bsin 2x-xcos 2x+xsin 2x
Teraz przechodzę do rozwiązania szczególnego, uwzględniając warunki początkowe y(pi)=2pi, y'(pi)=2pi.
Najpierw liczę pochodną z rozwiązania ogólnego:
{y}'=left( 2x-2A+1 right)sin 2x+left( 2x+2B-1 right)cos 2x(obliczenia)
Teraz do rozwiązania ogólnego i do jego pochodnej wstawiam wartości z warunków początkowych otrzymując układ równań:
{ begin{matrix}
& 2pi =Acos 2pi +Bsin 2pi -pi cos 2pi +pi sin 2pi
& 2pi =left( 2pi -2A+1 right)sin 2pi +left( 2pi +2B-1 right)cos 2pi end{matrix}
cos 2pi =1i sin 2pi =0, zatem:
{ begin{matrix}
& 2pi =A-pi
& 2pi =2pi +2B-1 end{matrix}
{ begin{matrix}
& A=3pi
& B=frac{1}{2} end{matrix}
Podstawiając tak obliczone stałe do rozwiązania ogólnego mam rozwiązanie szczególne przy danych warunkach początkowych:
{{y}_{SZ}}=3pi cos 2x+frac{1}{2}sin 2x-xcos 2x+xsin 2x
KONIEC
Polecam też moje:
Kurs Video Równań Różniczkowych
Marcin
Witam czy pomoze ktos rozwiazac rownanie
1/5*y’+y=-3*x^2*e^(3x-1)+2/5*cos2x
Maciej
Witam. Mógłbym prosić o pomoc z równaniem:
(x*siny +y+2x)dx + ((x^2)*cosy + x*ln(x))dy = 0
Nasz docent ma fantazję 😛