Rozwiązując zadania z liczb zespolonych należy mieć na uwadze, że liczba zespolona w postaci trygonometrycznej wygląda tak:
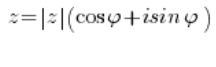
I tylko tak. Nie mniej, nie więcej.
Należy więc zwrócić uwagę na:
Kiedy liczba zespolona jest, a kiedy nie jest w postaci trygonometrycznej?
- Liczba:
 JEST liczbą w postaci trygonometrycznej, w której moduł z liczby równy jest 1 (
JEST liczbą w postaci trygonometrycznej, w której moduł z liczby równy jest 1 ( ), bo oczywiście:
), bo oczywiście:

- Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus.
Aby przekształcić tą liczbę do postaci trygonometrycznej, należy skorzystać ze wzorów trygonometrycznych:

Korzystając z tych wzorów możemy przekształcić:
Funkcje sinus i cosinus są -okresowe, zatem ich wartość jest taka sama co
-okresowe, zatem ich wartość jest taka sama co  . Więcej na ten temat napisałem w: tym poście.
. Więcej na ten temat napisałem w: tym poście.
Mamy więc na koniec:

…a to już JEST liczba w postaci trygonometrycznej. - Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus, oraz przed kosinusem jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus, oraz przed kosinusem jest minus, a powinien być plus.
Aby przekształcić tą liczbę zespoloną do postaci trygonometrycznej, należy wyłączyć minus przed nawias:

Zamienić na boku liczbę na postać trygonometryczną (to już chyba umiemy…):
na postać trygonometryczną (to już chyba umiemy…):

A więc mamy mnożenie dwóch liczb w postaci trygonometrycznej:
A mnoży się liczby w postaci trygonometrycznej mnożąc ich moduły i dodając argumenty (jest na to wzór), mamy więc:

To już zaś JEST liczba w postaci trygonometrycznej. - Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest minus, a powinien być plus.
Aby przekształcić tą liczbę zespoloną do postaci trygonometycznej, należy wyłączyć minus przed nawias:

Liczbę -1 należy zamienić na postać trygonometryczną (robiliśmy to w punkcie 3), tak samo na postać trygonometryczną należy zamienić liczbę (robiliśmy to w 2.).
(robiliśmy to w 2.).
Otrzymamy:

Czyli wykorzystując wzór na mnożenie funkcji trygonometrycznych:

I wykorzystując okresowość funkcji sinus i kosinus:
okresowość funkcji sinus i kosinus:

- Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest jednostka urojona 'i’ (a nie powinno jej tam być), a przed sinusem nie ma jednostki urojonej 'i’.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest jednostka urojona 'i’ (a nie powinno jej tam być), a przed sinusem nie ma jednostki urojonej 'i’.
Należy skorzystać ze znanych ze szkoły średniej wzorów trygonometrycznych:

Mamy więc:

A to już JEST liczba zespolona w postaci trygonometrycznej. - Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.
Należy zamienić sinus z cosinusem tak jak zostało to zrobione w 5., a potem rozwiązać tak jak w 4. - Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.
Należy zamienić sinus z cosinusem tak jak zostało to zrobione w 5., a potem rozwiązać tak jak w 2. - Liczba:
 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.
Należy zamienić sinus z cosinusem tak jak zostało to zrobione w 5., a potem rozwiązać tak jak w 3.
Powodzenia! 🙂


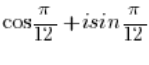 JEST liczbą w postaci trygonometrycznej, w której moduł z liczby równy jest 1 (
JEST liczbą w postaci trygonometrycznej, w której moduł z liczby równy jest 1 (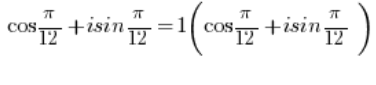
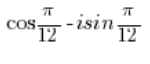 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus.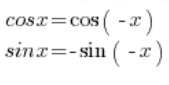
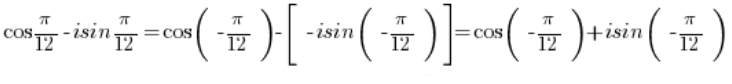
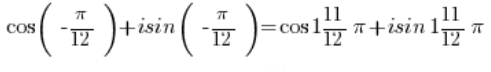
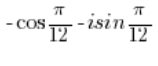 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus, oraz przed kosinusem jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed jednostką urojoną 'i’ pomnożoną przez sinus jest minus, a powinien być plus, oraz przed kosinusem jest minus, a powinien być plus.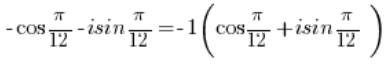
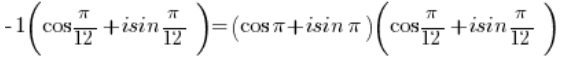
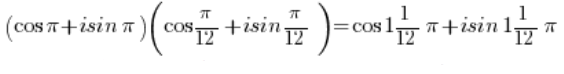
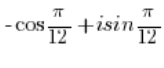 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest minus, a powinien być plus.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest minus, a powinien być plus.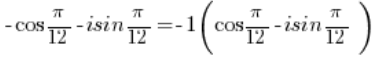
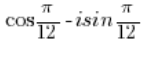 (robiliśmy to w 2.).
(robiliśmy to w 2.).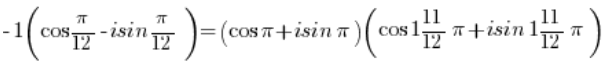
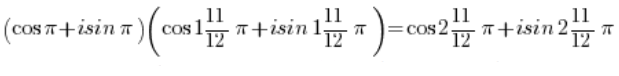
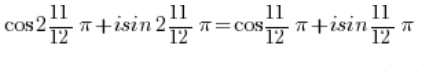
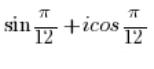 NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest jednostka urojona 'i’ (a nie powinno jej tam być), a przed sinusem nie ma jednostki urojonej 'i’.
NIE JEST liczbą zespoloną w postaci trygonometrycznej, bo przed kosinusem jest jednostka urojona 'i’ (a nie powinno jej tam być), a przed sinusem nie ma jednostki urojonej 'i’.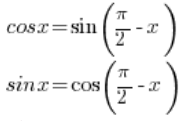
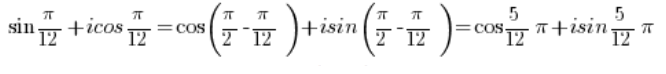
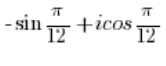 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.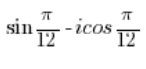 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.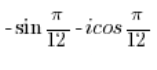 NIE JEST liczbą zespoloną w postaci trygonometrycznej.
NIE JEST liczbą zespoloną w postaci trygonometrycznej.