W artykule przedstawię, w jaki sposób rząd macierzy wykorzystywać można w rozwiązywaniu układów równań liniowych metodą Kroneckera-Capellego (bardziej prawidłowo: metodą wykorzystującą twierdzenie Kroneckera-Capellego). W artykule zakładam, że wiesz już, jak się liczy rząd macierzy i układy równań wzorami Cramera.
Twierdzenie Kroneckera-Capellego
Twierdzenie Kroneckera-Capellego wykorzystujące rząd macierzy jest naprawdę bardzo proste. Mając dowolny (to jest super-istotne, znaczy, że niewiadomych nie musi być tyle samo, co równań) układ równań:
Nasz układ – zwróć uwagę – ma m równań i n niewiadomych. Rząd macierzy głównej to rząd macierzy utworzonej ze współczynników przy niewiadomych, czyli:
Oczywiście nie musi to być macierz kwadratowa. Rząd macierzy uzupełnionej to rząd macierzy utworzonej ze współczynników przy niewiadomych z dodaną kolumną wyrazów wolnych (po prawych stronach równości):
Twierdzenie Kroneckera-Capellego stwierdza, że układ ma rozwiązania wtedy i tylko wtedy, gdy rząd macierzy głównej równy jest rzędowi macierzy uzupełnionej:
Z twierdzenia wynikają następujące wnioski:
Jeżeli rząd macierzy głównej, rząd macierzy uzupełnionej i liczba niewiadomych w układzie są równe () to układ równań ma dokładnie jedno rozwiązanie.
Jeżeli rząd macierzy głównej jest taki sam jak rząd macierzy uzupełnionej, ale jest mniejszy od liczby niewiadomych () to układ równań ma nieskończenie wiele rozwiązań.
Jeżeli rząd macierzy głównej jest różny od rzędu macierzy uzupełnionej (), wtedy układ równań nie ma rozwiązań.
Zastosowanie twierdzenia Kroneckera-Capellego (metoda rozwiązania układu równań)
Twierdzenie znamy. Pozostaje kwestia, jak zastosować je w praktyce.
Najbardziej “czystą” (ale niestety także czasochłonną) metodą jest policzenie po prostu obu rzędów (rzędu macierzy głównej i rzędu macierzy uzupełnionej ) zupełnie osobno, na końcu interpretacja wyniku, “obcięcie” układu do układu Cramera (poprzez ewentualne wykreślenie niektórych równań i zastąpienie niektórych zmiennych parametrami) i rozwiązanie otrzymanego układu Cramera. Tą metodę pokażę Tobie dalej w artykule.
Można też liczyć oba rzędu jednocześnie na jednej macierzy, można jednocześnie zerować wiersze lub kolumny, można liczyć właściwie metodą Gaussa… Czasem wydaje mi się, że ile profesorów tyle metod. Oczywiście, wszystkie są dobre, o ile prowadzą do celu, jakim jest rozwiązanie układu.
Przykład
Mamy do rozwiązania powyższy układ równań. Najpierw oczywiście sprawdzamy, czy nie jest to układ Cramera, tzn. czy ma tyle samo równań, co niewiadomych i czy wyznacznik główny układu jest różny od zera. Oczywiście nie jest to układ Cramera, bo mamy w nim 3 równania i 4 niewiadome. Układu nie rozwiązujemy więc w tej chwili wzorami Cramera, tylko przechodzimy do rzędów macierzy i twierdzenia Kroneckera-Capellego.
Na początku liczymy rząd macierzy głównej, czyli:
Liczymy, liczymy, liczymy, tak jak się liczy rzędy macierzy (zapraszam na przykład do mojego Kursu – to jest naprawdę proste) i mamy wynik:
Teraz liczymy rząd macierzy uzupełnionej:
Liczymy, liczymy, liczymy i mamy wynik:
Mamy zatem sytuację:
Rząd macierzy głównej jest równy rzędowi macierzy uzupełnionej i są one równe 3 (to istotne). Czyli układ będzie miał rozwiązanie i liczymy dalej. Piszemy jeszcze raz macierz główną:
A teraz wybieramy z niej jakikolwiek wyznacznik stopnia . W naszym przypadku rząd macierzy głównej i uzupełnionej wyszedł równy 3, czyli wybieramy jakikolwiek wyznacznik 3-go stopnia – ale uwaga – musi to być wyznacznik różny od zera (trzeba policzyć i sprawdzić na boku). Wybrany wyznacznik bierzemy w ramkę:
Teraz tworzymy układ równań wyłącznie z równań, których wiersze znalazły się w naszym wyznaczniku (pozostałe równania nie piszemy w ogóle) oraz wyłącznie z niewiadomych, których kolumny znalazły się w naszym wyznaczniku (pozostałe niewiadome zastępujemy parametrami).
W naszym przykładzie utworzymy układ równań składający się z równania pierwszego, drugiego i trzeciego (bo pierwszy, drugi i trzecie wiersz znalazły się w wyznaczniku):
Tak się składa, że będą to wszystkie równania.
Co do niewiadomych, patrzymy na kolumny, które dostały się do wybranego wyznacznika:
Jest to pierwsza, druga i trzecia niewiadoma: . “Nie załapała się” czwarta niewiadoma, czyli . Zastępujemy ją parametrem: gdzie przyjmuje dowolną wartość, czyli . Parametry można oznaczać różnymi innymi literkami, np “t”, można też nie oznaczać je literkami w ogóle, tylko po prostu zacząć traktować je jako parametry bez zmiany oznaczeń.
Tworzymy nowy układ równań:
Parametry traktujemy w nim jak liczby, czyli przerzucamy na prawą stronę:
Jest to układ Cramera i rozwiązujemy go wzorami Cramera. Jak utworzyć wyznaczniki do kolejnych zmiennych? Po prostu potraktować na przykład: – jako jedną liczbę. Na przykład:
Czy jeżeli wiem jak obliczyć układ równań metodą Gaussa, to policzę każdy układ, czy są jakieś specjalne wyjątki w których jednak lepiej jest zastosować twierdzenie Kroneckera-Capellego?
> budujemy macierz uzupełnioną układu (pierwsze 4 klolumny tworzą macierz główną ozn. A, wszystkie razem tzn. 4 kolumny + 1 z wyrazami wolnymi tworzą macierz uzupełnioną ozn. U)
> zerujemy kolumny w macierzy głównej A tzn. tworzymy kolumny z jedynkami i zerami aby ustalić rząd macierzy A oraz macierzy U
Po przekształceniach dostajemy, że ; (liczba niewiadomych) a zatem układ ma nieskończenie wiele rozwiązań zależnych od jednego parametru (patrz Twierdzenie Kroneckera-Capellego). Parametr ten wprowadzamy za niewiadomą z drugiej kolumny czyli za y ->patrz ostatnia macierz.
W – wyznacznik macierzy głównej (czyli macierzy współczynników),
– wyznacznik macierzy, otrzymanej za pomocy zamiany w macierzy głównej kolumny pod numerem j na kolumnę współczynników wolnych (czyli stojących z prawej strony od znaka =)
Przypominam jeszcze, że wyznacznik 3-go stopnia liczymy wg “reguły trójkątów”:
Dobrze ,że udało mi się trafic na tą stronę. Faktycznie brakuje tej metody w kursach,ale znając material z innych lekcji nie powinno być problemu 🙂 Jak najbardziej polecam kursy e-trapez.
witam,
bardzo podoba mi się jasny sposób w jaki tłumaczy Pan matematykę.mam zakupiony cały kurs z macierzy i chciałabym zapytać czy w którejś z lekcji znajduje się objaśnienie tego twierdzenia?bo niestety póki co nie znalazłam tego twierdzenia w Pana lekcjach..
Co zrobić jeżeli podczas rozwiązywania układu równań metodą Capellego i kiedy dojdziemy już do zastosowania metody Cramera, wyznacznik główny będzie równał się 0?
Podczas stosowania Capellego, przy wyborze wyznacznika jest zastrzeżenie, że ten wyznacznik musi być różny od zera, tak tak to napisałem w artykule:
W naszym przypadku rząd macierzy głównej i uzupełnionej wyszedł równy 3, czyli wybieramy jakikolwiek wyznacznik 3-go stopnia – ale uwaga – musi to być wyznacznik różny od zera (trzeba policzyć i sprawdzić na boku).
Ten wyznacznik tworzy za chwilę właśnie wyznacznik główny układu Kramera, stąd to zastrzeżenie.
Witam, znalazłem pewną nieścisłość w Pana Kursie Macierzy, lekcja 5 (Rząd macierzy) minuta 17:30, gdyby wybrać do ‘wyzerowania’ wiersz pierwszy to byśmy otrzymali rząd macierzy:
-2 1 -3
-4 2 -2
-10 5 -15
z czego otrzymalibyśmy kolejny rząd macierzy
0 4
0 0
i koncowy wynik wyszedłby 4, a nie 3 tak jak na filmiku. Proszę, o odpowiedź bo nie wiem co teraz robić.
Witam
A co w sytuacji gdy R(A) i R(U) wynosi 3, ale są 4 równania i 4 niewiadome? I wyznacznik macierzy 4 stopnia oczywiście wynosi zero.
Np
6x-5y=1
3x+2y+9z+6w=4
5x+4x+3z-4w=2
4x+3y+6z-4w=3
Jak wykreśliłem trzeci wiersz i wszystko z “z” to wyszedł mi wynik ale nie wiem czy tak mozna…
Jeżeli bym nie zszedł na maciez trzeciego stopnia to bym nic nie obliczył bo wszędzie jest zero….
Witam
Jednak zauważyłem błąd w pierwszym wierszu, drugiej kolumnie. Zamiast -5 powinno być 5. I wtedy faktycznie rząd macierzy wynosi 3 a wyznacznik z minora 4 stopnia wynosi 0. I tu mam problem, bo z cramera już nie wylicze wprost. Układ ma rozwiązanie bo R(A) i R(U) są sobie równe. tylko nie wiem, czy pozbywamy się jakiegoś równania i jedną z niewiadomych traktujemy jako parametr???
… i szukamy w niej niezerowego podwyznacznika stopnia 3 ( bo takie nam wyszły rzędy głównej i uzupełnionej). Może to być jak najbardziej wyznacznik powstały przez wykreślenie trzeciego wiersza i trzeciej kolumny:
A co w przypadku kiedy możemy wykreślić wiersz, natomiast nie mamy do zastąpienia parametrem żadnej kolumny?
Przykład:
x – 2y = 3
-2x – y = 4
-3x + y = 1
Rozumiem że zaczynamy od rzędu, który w tym przypadku dla obu macierzy wynosi 2. Następnie weźmy Dwa pierwsze wiersze i kolumny, wyznacznik będzie różny od zera. Teraz kiedy wykreślimy trzecie równanie, które nie było używane zostanie nam
x – 2y = 3
-2x – y = 4
Natomiast gdzie tutaj wstawić ewentualną stałą? Problem może prozaiczny, ale chwilę główkowałem i nie mogę znaleźć odpowiedzi. 🙂
Mam pytanie. Mamy uklad rownan (2 rownania, 3 niewiadome) x+2y-3z=2
5x-y+z=1.
Rzedy macierzy glownej i uzupelnionej sa sobie rowne (rzA=rzU=2). Moj problem teraz dotyczy wyboru niezerowego wyznacznika 2×2. Wychodzi mi, ze rozwiazania zaleza od wyboru wyznacznika (jest kilka mozliwosci). Jak to mozliwe?
Można by na przykład pomnożyć pierwszy wiersz przez -2i dodać do drugiego, przez -3i dodać do trzeciego i przez -3i dodać do czwartego, uzyskując wyznacznik:
Moge prosic o wytłyamzcenie tego, w jaki sposób dodaje sie te wiersze zbey wyzerowac? Mozesz opisac to krok po kroku ? 🙂
Korzystamy z plików cookies w celu dostosowania jej treści, jeśli będziesz na nią wracał; stosowania narzędzi analitycznych (Google Analytics, Crazyegg); marketingowych (Google Ads, Facebook Ads); widgetów matematycznych (Wolfram|Alpha) oraz embedowania treści ze stron zewnętrznych (YouTube, Vimeo). Cookies funkcjonują przez okres do 24 miesięcy, chyba że wcześniej je wyczyścisz. Dostęp do cookies mają podmioty trzecie wskazane w nawiasach. Poprzez kliknięcie “Zaakceptuj wszystkie”, wyrażasz zgodę na użycie WSZYSTKICH ciasteczek. Możesz też dostosować swoje zgody modyfikując Ustawienia. Czytaj więcej
Używamy ciasteczek, aby ulepszyć funkcjonowanie strony eTrapez. Podzieliliśmy te ciasteczka na kategorie. Niektóre z nich uznaliśmy za "niezbędne". Przechowujemy je w Twojej przeglądarce, ponieważ zapewniają podstawowe funkcjonalności strony. Inne ciasteczka uznaliśmy za mniej ważne i przechowujemy je w Twojej przeglądarce tylko za Twoją zgodą. Masz możliwość zablokowania tych ciasteczek.
Ponadto, oprócz naszych własnych, wewnętrznych ciasteczek, używamy także ciasteczek zewnętrznych firm, takich jak Facebook, Google, Vimeo.
Niezbędne ciasteczka są potrzebne do podstawowego działania strony. Zapewniają najbardziej kluczowe funkcjonalności, zabezpieczenia i zgodność z wymogami prawnymi.
Wszystkie inne ciasteczka, które nie są niezbędne do funkcjonowania strony, w szczególności zbierające dane osobiste do celów analitycznych, reklamowych i innych. Wymagają zgody użytkownika strony internetowej.
Ciasteczka statystyczne są używane do badania tego, jak użytkownicy zachowują się na stronie internetowej. Pomagają dostarczać informacje o wskaźnikach takich jak liczba odwiedzin na stronie, współczynnik odrzuceń, źródła odwiedzin itd.
Ciasteczka reklamowe są używane do celów marketingowych. Śledzą wizyty użytkowników na stronach internetowych i zbierają informacją o ich zachowaniach, aby docierać do nich z odpowiednimi reklamami.
Ciasteczka wydajnościowe używane są do zrozumienia i analizy kluczowych indeksów strony, takich jak szybkość wyświetlania treści, liczba wyświetleń video itp. Dzięki nim możemy poprawiać stronę tak, żeby korzystanie z niej było bardziej przyjazne dla użytkowników.
Ciasteczka funkcjonalne pomagają wykonywać określone funkcje, takie jak udostępnianie treści strony na platformach mediów społecznościowych, zbieranie opinii oraz inne funkcje stron trzecich.
Jak rozwiązać takie zadanie:
Dany układ równań liniowych w zależności od parametru A
Omówiłem takie zadanka ogólnie tutaj:
https://blog.etrapez.pl/rzad-macierzy-w-ukladach-rownan-liniowych-z-parametrem/
jak policzyć takie równanie ?
x+y=3
x-y=-1
2x+y=4
Witam,jak policzyć taki wyznacznik z liczbą urojoną lub niewiadomą, sama nie wiem?i 1-1 i2i 2+i
I nie wyznacznik tylko rząd, pogubiłam się już 🙁
Czy jeżeli wiem jak obliczyć układ równań metodą Gaussa, to policzę każdy układ, czy są jakieś specjalne wyjątki w których jednak lepiej jest zastosować twierdzenie Kroneckera-Capellego?
Pomocy mam układ równań następujący :
-2x+2y+3u-w=1
-x+y-3z++u=-1
x-y-z+w=0
Problem w tym że nie wiem jak zacząć… Pilne na jutro do wyjaśnienia.
Układ równań (chyba zamiast u powinno być z

można rozwiązać następująco:
> budujemy macierz uzupełnioną układu (pierwsze 4 klolumny tworzą macierz główną ozn. A, wszystkie razem tzn. 4 kolumny + 1 z wyrazami wolnymi tworzą macierz uzupełnioną ozn. U)
> zerujemy kolumny w macierzy głównej A tzn. tworzymy kolumny z jedynkami i zerami aby ustalić rząd macierzy A oraz macierzy U
Po przekształceniach dostajemy, że
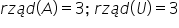

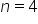
Z ostatniej macierzy odczytujemy rozwiązanie tzn.
czyli ostateczne rozwiązanie jest postaci
Jak powinienem \interpretować polecenie zadania:
“Wyznacz bazę przestrzeni kolumn macierzy A i rząd macierzy A”
Pomocy… Mam układ równań :
3x-y+z-4w=0 ,
-6x+2y-2z+8w=0
rzA=1 rzAU=1 nie wiem co mogę wziąć za parametr..
Pomocy, dlaczego rzA i rzU wychodzi mi rowny 2?
Co w momencie kiedy rzA=3 rzAU=3 ale mamy wiecej wierszy niż kolumn?
kiedy rza=rzu=n to zawsze bedzie uklad Cramera?
mam takie uklad rownan
x+y+t=0
2x-y-t=3
4x-5y-3t=7
rzA = rzU= 3 = n; wiem ze mamy jedno rozwiazanie,to dalej trzeba skreslic jedno rownanie? ale jest problem bo mamy 3 niewiadome.
Nic nie skreślamy i nie wybieramy parametrów. To jest układ Cramera, rozwiązujemy go po prostu wzorami Cramera.
Rozwiązanie:
Skorzystamy ze wzorów Cramera:
gdzie:
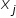

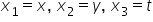
W – wyznacznik macierzy głównej (czyli macierzy współczynników),
Przypominam jeszcze, że wyznacznik 3-go stopnia liczymy wg “reguły trójkątów”:
Liczymy:
I analogiczne:
Wtedy:
Odp.: x=1, y=0, t=-1
dlaczego w tym ostatnim etapie wyszlo -8 + α , a nie -8 + 11α ?
Bardzo prosze o rozpisanie obliczenia wyznacznika x (przy macierzy gdzie jest \lambda) próbuje, to robić, ale wychodzą mi kosmiczne wyniki………
Dobrze ,że udało mi się trafic na tą stronę. Faktycznie brakuje tej metody w kursach,ale znając material z innych lekcji nie powinno być problemu 🙂 Jak najbardziej polecam kursy e-trapez.
Dzięki wielkie! W końcu jakieś konkretne tłumaczenie tej metody 🙂 Szkoda, że nie ma jej w kursach 🙂
Czy rozwiązywanie układów równań tą metodą jest gdzieś na kursie video? 🙂
a przepraszam juz bylo to pytanie:)
witam,
bardzo podoba mi się jasny sposób w jaki tłumaczy Pan matematykę.mam zakupiony cały kurs z macierzy i chciałabym zapytać czy w którejś z lekcji znajduje się objaśnienie tego twierdzenia?bo niestety póki co nie znalazłam tego twierdzenia w Pana lekcjach..
Nie, niestety, twierdzenia Kroneckera – Capellego nie ma Kursie…
witam, czy mógłby Pan w którymś z artykułów poruszyć kwestię programowania liniowego oraz metody symplex? pozdrawiam
Witam, niestety nie…
Jeżeli rząd(A) jest większy od rzędu(U), to z jakiego twierdzenia lub metod korzystamy?
To jest niemożliwe i nigdy się nie zdarzy 🙂
Witam, czy może Pan przedstawić jak wyliczyliśmy Wx1 ? Jeżeli Pan może to chciałbym poznać drogę do wyniku Wx1=-8+a1.
Pozdrawiam.
Również podpisuje się pod powyższą prośbą, proszę o pomoc.
jeśli sprawdzimy wyniki to wyjdzie: 1)2×1 – 3×2 + 5×3 + 7×4 = 2* -8+a/-16 – 3*0 + 5* 22a/-16 + 7a = -16 +2a + 110a – 112a = -16
Czemu wynik nie wyszedł 1? Zrobiłam błędy?
Co zrobić jeżeli podczas rozwiązywania układu równań metodą Capellego i kiedy dojdziemy już do zastosowania metody Cramera, wyznacznik główny będzie równał się 0?
Nigdy tak się nie stanie.
Podczas stosowania Capellego, przy wyborze wyznacznika jest zastrzeżenie, że ten wyznacznik musi być różny od zera, tak tak to napisałem w artykule:
Ten wyznacznik tworzy za chwilę właśnie wyznacznik główny układu Kramera, stąd to zastrzeżenie.
Super strona, świetnie wytłumaczone!!!
Faktycznie. Sam nie wiem jak mogłem to przeoczyć. Dziękuję.
Witam, znalazłem pewną nieścisłość w Pana Kursie Macierzy, lekcja 5 (Rząd macierzy) minuta 17:30, gdyby wybrać do ‘wyzerowania’ wiersz pierwszy to byśmy otrzymali rząd macierzy:
-2 1 -3
-4 2 -2
-10 5 -15
z czego otrzymalibyśmy kolejny rząd macierzy
0 4
0 0
i koncowy wynik wyszedłby 4, a nie 3 tak jak na filmiku. Proszę, o odpowiedź bo nie wiem co teraz robić.
Witam
A co w sytuacji gdy R(A) i R(U) wynosi 3, ale są 4 równania i 4 niewiadome? I wyznacznik macierzy 4 stopnia oczywiście wynosi zero.
Np
6x-5y=1
3x+2y+9z+6w=4
5x+4x+3z-4w=2
4x+3y+6z-4w=3
Jak wykreśliłem trzeci wiersz i wszystko z “z” to wyszedł mi wynik ale nie wiem czy tak mozna…
Jeżeli bym nie zszedł na maciez trzeciego stopnia to bym nic nie obliczył bo wszędzie jest zero….
Witam,
Ale rząd macierzy głównej tego układu…
\left[ \begin{matrix}
6 & -5 & 0 & 0 \\
3 & 2 & 9 & 6 \\
5 & 4 & 3 & -4 \\
4 & 3 & 6 & -4 \end{matrix} \right]
…jest równy 4 (zakładam, że w trzecim wierszu miał Pan literówkę)? Niech Pan sprawdzi w WolframAlpha .
Witam
Jednak zauważyłem błąd w pierwszym wierszu, drugiej kolumnie. Zamiast -5 powinno być 5. I wtedy faktycznie rząd macierzy wynosi 3 a wyznacznik z minora 4 stopnia wynosi 0. I tu mam problem, bo z cramera już nie wylicze wprost. Układ ma rozwiązanie bo R(A) i R(U) są sobie równe. tylko nie wiem, czy pozbywamy się jakiegoś równania i jedną z niewiadomych traktujemy jako parametr???
Dobra, czyli mamy układ…
\{ \begin{matrix}
& 6x+5y=1 \\
& 3x+2y+9z+6w=4 \\
& 5x+4y+3z-4w=2 \\
& 4x+3y+6z-4w=3 \end{matrix}
… i policzyliśmy już, że rząd macierzy głównej = rząd macierzy uzupełnionej = 3.
Dalej bierzemy macierz główną…
\left[ \begin{matrix}
6 & 5 & 0 & 0 \\
3 & 2 & 9 & 6 \\
5 & 4 & 3 & -4 \\
4 & 3 & 6 & -4 \end{matrix} \right]
… i szukamy w niej niezerowego podwyznacznika stopnia 3 ( bo takie nam wyszły rzędy głównej i uzupełnionej). Może to być jak najbardziej wyznacznik powstały przez wykreślenie trzeciego wiersza i trzeciej kolumny:
\left| \begin{matrix}
6 & 5 & 0 \\
3 & 2 & 6 \\
4 & 3 & -4 \end{matrix} \right|=24
… bo jest on różny od zera.
Teraz trzecie równanie wykreślamy, a zmienną zz trzeciej kolumny ani nie pomijamy, ani nie przyjmujemy, że równa się 0, tylko zastępujemy parametrem.
Przyjmujemy więc, że:
z=\alpha
… i wychodzimy na układ:
\{ \begin{matrix}
& 6x+5y=1 \\
& 3x+2y+9\alpha +6w=4 \\
& 4x+3y+6\alpha -4w=3 \end{matrix}
\alphanie jest niewiadomą, zmienną, tylko stałą, przerzucamy go więc na prawo do stałych i mamy:
\{ \begin{matrix}
& 6x+5y=1 \\
& 3x+2y+6w=4-9\alpha \\
& 4x+3y-4w=3-6\alpha \end{matrix}
Ten układ można rozwiązać np. wzorami Cramera. Dostaniemy:
\{ \begin{matrix}
& x=6-15\alpha \\
& y=18\alpha -7 \\
& z=\alpha \\
& w=0,\quad \alpha \in R \end{matrix}
Co zgadza się z wynikiem w WolframAlpha 🙂
Aha. Dziękuję za odpowiedź.
A co w przypadku kiedy możemy wykreślić wiersz, natomiast nie mamy do zastąpienia parametrem żadnej kolumny?
Przykład:
x – 2y = 3
-2x – y = 4
-3x + y = 1
Rozumiem że zaczynamy od rzędu, który w tym przypadku dla obu macierzy wynosi 2. Następnie weźmy Dwa pierwsze wiersze i kolumny, wyznacznik będzie różny od zera. Teraz kiedy wykreślimy trzecie równanie, które nie było używane zostanie nam
x – 2y = 3
-2x – y = 4
Natomiast gdzie tutaj wstawić ewentualną stałą? Problem może prozaiczny, ale chwilę główkowałem i nie mogę znaleźć odpowiedzi. 🙂
mam takie uklad rownan
x+y+t=0
2x-y-t=3
4x-5y-3t=7
rzA = rzU= 3 = n; wiem ze mamy jedno rozwiazanie,to dalej trzeba skreslic jedno rownanie? ale jest problem bo mamy 3 niewiadome.
Mam pytanie. Mamy uklad rownan (2 rownania, 3 niewiadome) x+2y-3z=2
5x-y+z=1.
Rzedy macierzy glownej i uzupelnionej sa sobie rowne (rzA=rzU=2). Moj problem teraz dotyczy wyboru niezerowego wyznacznika 2×2. Wychodzi mi, ze rozwiazania zaleza od wyboru wyznacznika (jest kilka mozliwosci). Jak to mozliwe?
Te rozwiązania są równoważne 🙂 Tutaj nakręciłem filmik na ten temat:
Super. Dziekuje bardzo za wytlumaczenie przykladu. Teraz wszystko jasne i klarowne 🙂
musisz wyzerować kolumne i wykreślić ją razem z wierszem tak aby otrzymać macierz 3×3
Witam jak policzyć rozwinięcie Laplace’a wyznacznika:
3 13 17 4
6 28 33 8
10 40 54 13
8 37 46 11
Można by na przykład pomnożyć pierwszy wiersz przez -2i dodać do drugiego, przez -3i dodać do trzeciego i przez -3i dodać do czwartego, uzyskując wyznacznik:
\left| \begin{matrix}
3 & 13 & 17 & 4 \\
0 & 2 & -1 & 0 \\
1 & 1 & 3 & 1 \\
-1 & -2 & -5 & -1 \end{matrix} \right|
Teraz – znowu na przykład – bierzemy trzeci, mnożymy przez -3i dodajemy do pierwszego i przez 1i dodajemy do czwartego, uzyskując:
\left| \begin{matrix}
0 & 10 & 8 & 1 \\
0 & 2 & -1 & 0 \\
1 & 1 & 3 & 1 \\
0 & -1 & -2 & 0 \end{matrix} \right|
Rozwijamy teraz względem pierwszej kolumny i mamy:
\left| \begin{matrix}
0 & 10 & 8 & 1 \\
0 & 2 & -1 & 0 \\
1 & 1 & 3 & 1 \\
0 & -1 & -2 & 0 \end{matrix} \right|={{\left( -1 \right)}^{3+1}}\cdot 1\cdot \left| \begin{matrix}
10 & 8 & 1 \\
2 & -1 & 0 \\
-1 & -2 & 0 \end{matrix} \right|
Ten wyznacznik można już Sarrusem, ale można zauważyć sprytnie, że trzecia kolumna jest wyzerowana i rozwinąć ją jeszcze raz Laplace’m:
\left| \begin{matrix}
0 & 10 & 8 & 1 \\
0 & 2 & -1 & 0 \\
1 & 1 & 3 & 1 \\
0 & -1 & -2 & 0 \end{matrix} \right|={{\left( -1 \right)}^{3+1}}\cdot 1\cdot \left| \begin{matrix}
10 & 8 & 1 \\
2 & -1 & 0 \\
-1 & -2 & 0 \end{matrix} \right|=1\cdot {{\left( -1 \right)}^{1+3}}\left| \begin{matrix}
2 & -1 \\
-1 & -2 \end{matrix} \right|
=1\cdot {{\left( -1 \right)}^{1+3}}\left| \begin{matrix}
2 & -1 \\
-1 & -2 \end{matrix} \right|=1\cdot \left( -5 \right)=-5
Na końcu jeszcze sprawdzić można wynik:
Wynik w WolframAlpha
(polecam mój Poradnik do niego)
Moge prosic o wytłyamzcenie tego, w jaki sposób dodaje sie te wiersze zbey wyzerowac? Mozesz opisac to krok po kroku ? 🙂