W tym artykule przedstawię metodę rozwiązywania układów równań liniowych, zwaną “metodą macierzy odwrotnej”. Można ją śmiało dołączyć do znanych metod: Cramera, Kroneckera-Capellego (ta stanowi właściwe przejście na metodę Cramera) i Gaussa.
Zastrzegamy od razu, że metodę macierzy odwrotnej można stosować tylko w układach równań liniowych Cramera, tzn. takich, w których:
- Jest tyle samo równań, co niewiadomych
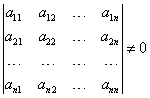
- Wyznacznik główny układu (złożony ze współczynników przy zmiennych) jest różny od zera
1. Przypadek ogólny
Na czym polega metoda? Weźmy układ równań, spełniający powyższe założenia:
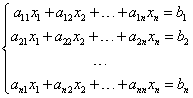
Układ ma tyle samo równań, co niewiadomych (n równań i n niewiadomych), a jego wyznacznik główny jest różny od zera:
Powyższy układ równań można zapisać jako mnożenie następujących macierzy:
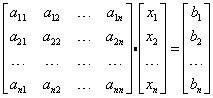
Nie wierzysz? Sprawdź sam, mnożąc sobie w odpowiedniej tabelce macierze
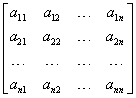
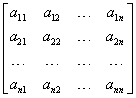
![]()
![]()


Po przemnożeniu pierwszego wiersza przez pierwszą (i jedyną, oczywiście) kolumnę otrzymamy:
![]()
![]()
![]()
![]()



Aby go rozwiązać, mnożymy go obustronnie przez 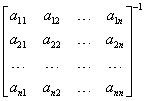
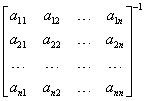
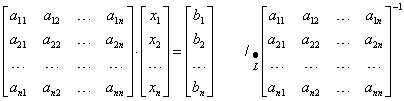
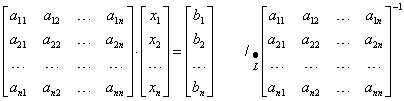
Zwracamy uwagę, że mnożymy obie strony, ale od strony lewej, bo macierz współczynników jest po lewej stronie macierzy niewiadomych. Macierz odwrotna będzie istnieć, bo jej wyznacznik jest różny od zera, co zapewniliśmy sobie w założeniach (to jest układ Cramera). Wychodzimy więc na:


Teraz pozostaje nam już tylko wyliczyć macierz odwrotną: 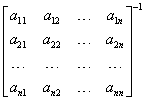
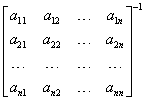
przemnożyć ją przez macierz: ![]()
![]()
…i otrzymamy macierz wynikową:
![]()
![]()
2. Przykład
Weźmy konkretny układ równań liniowych:
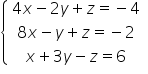
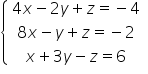
Na początku zapisujemy postać macierzową tego układu: 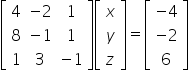
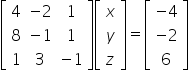
Zauważmy, że w macierzy pierwszej od lewej są współczynniki przy zmiennych układu, potem jest macierz niewiadomych (jednokolumnowa), a po prawej stronie macierz wyrazów wolnych. Teraz wystarczy rozwiązać to równanie tak jak się rozwiązuje równania macierzowe, tzn.:
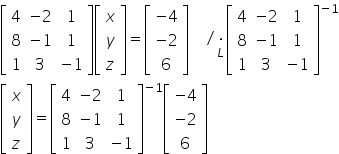
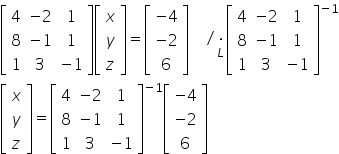
Potem policzyć macierz odwrotną: 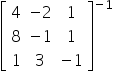
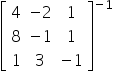
powinna nam wyjść: 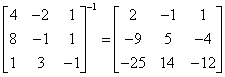
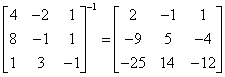
i przemnożyć ją przez: 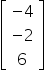

…powinniśmy wtedy wyjść na wynik:
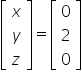
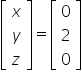
Pozostaje teraz już tylko zapisać odpowiedź:
Odp. 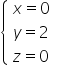
3. Podsumowanie
Metoda macierzy odwrotnej ma zaletę polegającą na tym, że żeby się jej nauczyć nie potrzebujesz zbyt wielu nowych wiadomości oprócz umiejętności liczenia macierzy odwrotnych i rozwiązywania równań macierzowych.
Jej wadą jest natomiast duża żmudność obliczeń i ograniczenie do układów Cramera.
Układy równań, które mają więcej niż trzy równania i niewiadome wymagają obliczenia macierzy odwrotnych większych, niż ![]()
![]()
Metoda Gaussa-Jordana obliczania macierzy odwrotnej (następny Wykład) –>


A czy w macierzy odwrotnej nie powinno być -2 (na pozycji 11)?
(-1)^2 pomnożone przez wyznacznik czyli -2 = 1* (-2) = -2
Dzięki za czujność, ale dobrze jest.
We wzorze na macierz odwrotną mnoży się jeszcze na początku przez
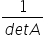
U nas
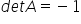

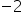

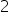
Witam Mam problem z zadaniem o treści :Podaj liczbę rozwiązań następującego układu równań w zalezności od parametru:a-alfaax+y+2z=1x+ay+2z=qx+y+2az+1Pomógłby mi ktoś ? Z góry dziękuje 🙂
Źle sie sformatowało. Powinno wyglądać takax+y+2z=1. x+ay+2z=1.x+y+2az=1.
Jak pomnożyć macierz 1×1 (tutaj {{4}{-2}{6}} z macierzą 3×3? Chodzi mi o ten moment prawie na samym końcu przykładu 2, kiedy mamy już zrobioną macierz odwrotną i mnożymy ją przez ww 1×1?
Już wiem, chwilowe zaćmienie umysłu, wszystko się zgadza. Przepraszam, za wprowadzenie zamieszania!
jakie są zasady zapisu wektora (15, 28, 18) jako [-15, 28, 18] = 4[1, 2, 3] + 5 [-3, 4, 2] – 4[1, 0, 1].
treść zadania :
Znajdź współrzędne wektora [-15, 28, 18] w bazie złożonej z wektorów: [1, 2, 3], [-3, 4, 2], [1, 0, 1].
Wektor [-15, 28, 18] zapisujemy jako:
[-15, 28, 18] = 4[1, 2, 3] + 5 [-3, 4, 2] – 4[1, 0, 1].
A zatem współrzędnymi wektora [-15, 28, 18] w tej bazie są liczby [4, 5, – 4].
Jak rozumiem, współrzędnych [4, 5, – 4] nie mamy danych na początku zadania, tylko mamy je dopiero policzyć.
Tworzymy równość, wyrażając wektor [15,28,18] przy pomocy sumy wektorów z bazy przemnożoną przez jakieś niewiadome stałe:
[-15,28,18]=\alpha \left[ 1,2,3 \right]+\beta \left[ -3,4,2 \right]+\gamma \left[ 1,0,1 \right]
[-15,28,18]=\left[ \alpha ,2\alpha ,3\alpha \right]+\left[ -3\beta ,4\beta ,2\beta \right]+\left[ \gamma ,0,\gamma \right]
[-15,28,18]=\left[ \alpha -3\beta +\gamma ,2\alpha +4\beta ,3\alpha +2\beta +\gamma \right]
Aby wektory po lewej i prawej były równe, muszą zachodzić równości (układ równań):
\{ \begin{matrix}
& -15=\alpha -3\beta +\gamma \\
& 28=2\alpha +4\beta \\
& 18=3\alpha +2\beta +\gamma \end{matrix}
Układ ten rozwiązać można np. wzorami Cramera (daruję już to sobie i podam od razu rozwiązanie):
\{ \begin{matrix}
& \alpha =4 \\
& \beta =5 \\
& \gamma =-4 \end{matrix}
Zatem zachodzi równość:
[-15,28,18]=4\left[ 1,2,3 \right]+5\left[ -3,4,2 \right]-4\left[ 1,0,1 \right]
Odp. Wektor [-15,28,18]w bazie złożonej z wektorów [1,2,3], [-3,4,2], [1,0,1]miałby współrzędne [4,5,-4].
Każdy układ równań liniowych można sprowadzić do układu Cramera , więc to nie jest jakieś tam ograniczenie