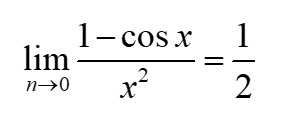
Przydatna granica funkcji z cosinusem
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Granice funkcji z sinusem zwykle traktujemy wzorem: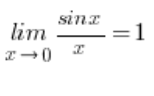 
(wyprowadzenie tego wzoru możesz znaleźć tutaj).
Pytanie: co z cosinusem x?
Wzór na granicę funkcji z cosinusem
Oczywiście nie zachodzi: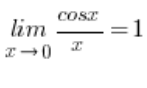 
, bo granica funkcji 
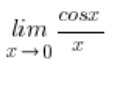nie jest w ogóle symbolem nieoznaczonym.
Do granic z cosinusem x często pomocny bywa wzór:
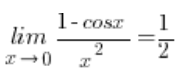– w wielu podręcznikach podany już “na starcie”, bez wykazywania, a w wielu jako granica funkcji, którą trzeba dopiero wyliczyć.
Niezależnie od tego, jak jest w Twoim przypadku, warto znać sposób wyprowadzenia tego wzoru, a leci to tak:
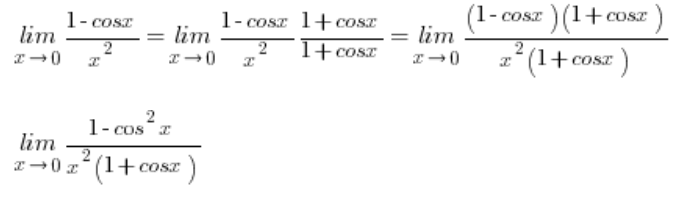
W tym momencie w liczniku korzystam z jedynki trygonometrycznej:
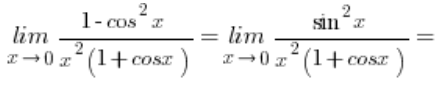
Granica funkcji z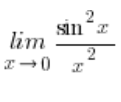 
zbiega do 
, bo:
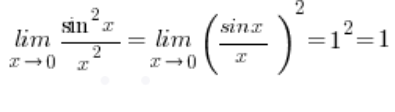
A granica funkcji z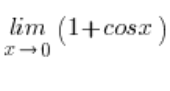 
zbiega do 
, bo 
, zatem mamy wynik:
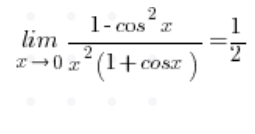
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Panie Karczyński, idź Pan na księdza to za 100 lat zostanie Pan mianowany patronem studentów
Z koleżanką oglądamy regularnie i baaaardzo nam to pomaga w zrozumieniu matematyki na studiach szczególnie że mamy kiepskie podstawy a czasu brak na ich ogarnięcie 🙁
Kursy są robione w sposób jasny, zrozumiały i co najwazniejsze są tłumaczone językiem zrozumiałym dla studentów.
p.s. Przydałby się w rozwiązaniach zadań domowych(o ile to możliwe) pokazywać jednak przykładowy sposób jak się do tego doszło. Wiem ze to dużo więcej roboty dla Pana ale myślę że ułatwiłoby znacznie prace studen\tom 🙂
Pozdrawiam!
Kocham matematykę <3 Dzięki Krystian!
Zgadza się, ale wtedy trzeba znać pochodne. No i Pan Profesor musi pozwolić.
dziekuje…z a to wyprowadzenie … Pani dr nie potrafila ogarnąć ale madrzy studenci Politechniki Wrocławskiej wytlumaczyli
A jak będzie ze zbieżnością takiego szeregu n*sin (1/n2)?
bardzo fajnie wytłumaczone,ale mam jeden problem :/ co zrobić gdy w mianowniku jest 3x^2 zamiast samego x^2
Kurs niesamowity, bardzo mi pomógł. Tłumaczenie nie jest sztywne i przyjemnie się Pana słucha 😉 Pozdrawiam!
Dzięki!
Kurs pierwszorzędny! Zagadnienia wytłumaczone bardzo precyzyjnie, różne stopnie trudności.
polecam 🙂
Genialne
Takie łatwe a sam bym tego nie ogarnął
Genialne
Bardzo, bardzo dziękuję Panu za wytłumaczenie! Miałam właśnie w podręczniku zadanko, w którym trzeba było to obliczyć – dobrze, że jest taki ktoś jak Pan 😉
Super, cieszę się, że się przydało.