Granice funkcji Wykład 6
Temat: Granice funkcji – definicja Cauchy’ego
Streszczenie
W artykule przedstawię drugą definicję granicy funkcji – tzw. definicję Cauchy’ego. W odróżnieniu od definicji Heinego, opierającej się na granicy ciągu, definicja Cauchy’ego bazuje na pojęciu tzw. “otoczenia punktu”. Przed przeczytaniem wypadało by wiedzieć, czym jest funkcja (przyporządkowanie argumentom wartości), argumenty i wartości funkcji i jak narysować ją na wykresie.
“Otoczenie punktu  ” – co to jest?
” – co to jest?
Z otoczeniem punktu ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()






Przypomnijmy sobie jeszcze ze średniej, jak przedziały liczbowe (a więc także otoczenia) opisać używając wartości bezwzględnej.
Przedział (3,5) to zbiór punktów, których odległość od 4 jest mniejsza od 1. Odległości zaś pomiędzy dwoma punktami oznaczyć można jako wartość bezwzględna z ich różnicy, zatem punkty x należące do otoczenia (3,5) to punkty x spełniające warunek: ![]()
![]()
Przedział zaś (3,5;4,5) to zbiór punktów x, których odległość od 4 jest mniejsza od 0,5, zatem można je opisać nierównością ![]()
![]()
Jaka nierówność zaś opisuje otoczenie (2,6)? Będzie to ![]()
![]()
Granice funkcji według Cauchy’ego – wprowadzenie
Definicja granic funkcji według Cauchy’ego opiera się właśnie na otoczeniach. Otoczeniach wartości funkcji i otoczeniach argumentów funkcji. Zanim zaatakujemy samą definicję, powiedzmy sobie, czym są otoczenia argumentów i odpowiadające im otoczenia wartości.
Weźmy funkcję:
![]()
![]()
![]()
wraz z jej wykresem:
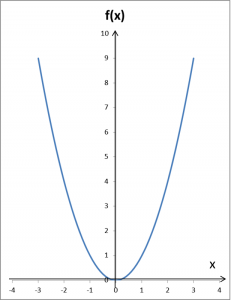

zaznaczmy na nim pewne otoczenie argumentów (czyli x-sów), na przykład (1,3):
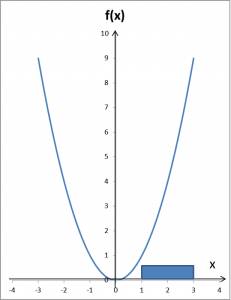

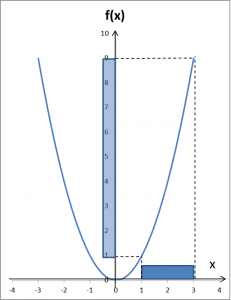

Definicja granicy funkcji
Skoro wiemy już, co to znaczy, że otoczeniu argumentów odpowiada jakieś otoczenie wartości możemy wytoczyć oficjalną definicję granicy funkcji wg. Cauchy’ego.
Liczbę g nazywamy granicą funkcji w punkcie ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dla każdego otoczenia (nawet bardzo małego) wartości funkcji g znajdziemy takie otoczenie argumentu funkcji ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Zamotane? Na pierwszy rzut oka na pewno tak.
Weźmy funkcję ![]()
![]()
![]()
![]()
![]()
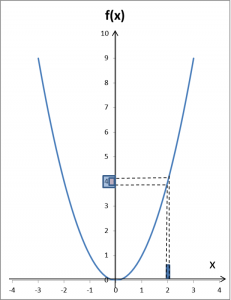
Oznacza to, że dla dowolnie małego otoczenia wartości 4… Powiedzmy na początek, że niech to będzie otoczenie (3,5):
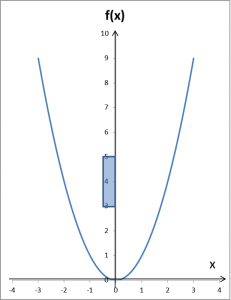

Zastanówmy się. Nie może to być otoczenie argumentów na przykład: (1,5;2,5):
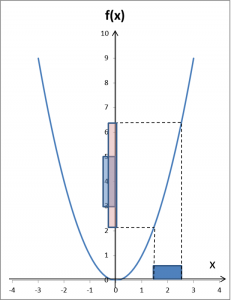

Musimy dobrać jakieś mniejsze otoczenie argumentu 2. Może (1,9;2,1)?
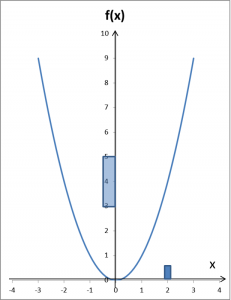

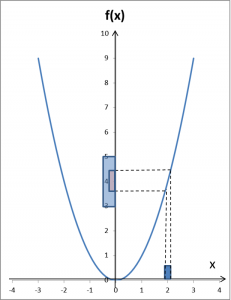

Na powyższym przykładzie można załapać, jak to działa. Teraz chodzi o to, że jak dowolnie małe otoczenie 4 wybrali byśmy na początku:
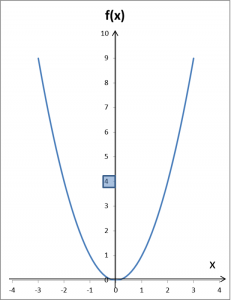


Formalny zapis definicji granicy funkcji
Zapiszmy teraz naszą definicję formalnym językiem symboli. Jak pamiętamy, otoczeniem wartości 4 o długości 1 mogliśmy zapisać przedziałem (3,5), a mogliśmy też wartością bezwzględną: ![]()
![]()
![]()
![]()
Definicja granicy funkcji zapisana symbolami wyglądać będzie tak:
Liczbę g nazywamy granicą funkcji w punkcie ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
KONIEC
Kliknij, aby przypomnieć sobie, jaka jest definicja granicy funkcji Heinego (poprzednie Wykład) <–
Kliknij, aby zobaczyć jak wykorzystywać granice funkcji z definicji w praktyce (następny Wykład) –>


Ostatechna definicja jest źle podana, podana dedinicja to definicja granicy lewostronnej w danym punkcie. Powinno wyglądać to tak (kwantyfikatory są wporządku |x-x0||F(x)-g|<E) .
Tam gdzie skraca się zera przez kreskę ułamkową kończy sie matematyka a zaczyna tfu “nauczanie”
Mam taką zagwozdkę;
pisze Pan “Liczbę g nazywamy granicą funkcji w punkcie x_0, jeśli:
Dla każdego otoczenia (nawet bardzo małego) wartości funkcji g znajdziemy takie otoczenie argumentu funkcji x_0, że odpowiadające im otoczenie wartości zawiera się w tym ustalonym na początku (nawet bardzo małym) otoczeniu wartości funkcji g.”
Powiedzmy ,że mamy funkcję f(x)=x ,sigma=1 i epsilon=1.i mamy daną granicę w punkcie x0=2 g=2.I teraz jak narysujemy sobie wykres to zobaczymy ,że otoczenie punktu x0 nie zawiera się w otoczeniu g tylko mu odpowiada ,ale za to spełnione jest równanie:
0<I x-x0 I I f(x)-g I<epsilon.Reasumując według cytatu powyżej otoczenie argumentu x0(w tym przypadku) nie zawiera się w otoczeniu g ,ale za to według definicji już tak.Proszę o rozjaśnienie sytuacji.
Pozdrawiam