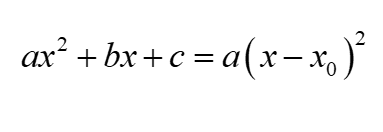
Delta równa zero w całkach nieoznaczonych wymiernych

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Rozkład na czynniki trójmianu kwadratowego

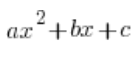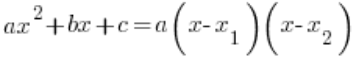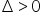W całkach nieoznaczonych wymiernych zachodzi (często) konieczność rozkładu na czynniki trójmianu kwadratowego: . Robimy to oczywiście ze wzoru: , który działa wtedy, gdy $increment greater than 0$ .

Jak wygląda jednak ten dwumian, gdy delta równa jest konkretnie i dokładnie ? Na przykład jak wyglądać będzie rozłożone na czynniki: (, )?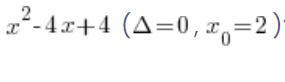

Czy może tak: ?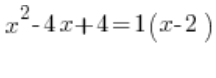

Oczywiście nie… Ze szkoły średniej pamiętamy, że jeśli wychodził nam faktycznie jeden pierwiastek, ale był to pierwiastek podwójny. Zatem w naszym przykładzie można powiedzieć, że: , czyli trójmian kwadratowy rozłożony na czynniki wyglądać będzie tak:

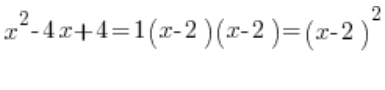
Ma to spore konsekwencje w całkach nieoznaczonych wymiernych przy okazji rozkładu na ułamki proste. Weźmy przykład:

$int{}{}{dx/{2x^3+4x^2+2x}}$

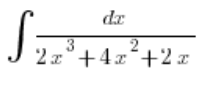
Rozbieramy na boczku sam ułamek bez całki, czyli piszemy:

$1/{2x^3+4x^2+2x}$

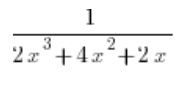
Na dole wyciągamy x przed nawias:

$1/{2x^3+4x^2+2x}=1/{x(2x^2+4x+2)}$

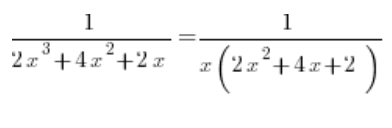
Z trójmianu kwadratowego na dole liczymy deltę, wychodzi , oraz pierwiastek – wychodzi . Rozkładając na czynnik uzyskujemy więc:

$1/{2x^3+4x^2+2x}=1/{x(2x^2+4x+2)}=1/{x2(x+1)(x+1)}=1/{2x(x+1)^2}$

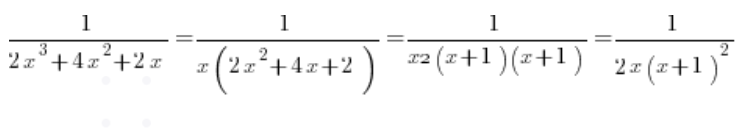
A rozkładając na ułamki proste:

$1/{2x(x+1)^2}=A/{2x}+B/{x+1}+C/(x+1)^2$

Bestsellery w tym miesiącu

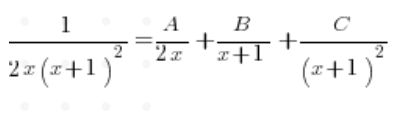
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?

Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.

Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.

Dodaj komentarz Anuluj pisanie odpowiedzi

Cookie	Duration	Description
_ce.cch	session	No description
_ce.s	1 year	No description
_koko_analytics_pages_viewed	6 hours	No description available.
cebsp	session	No description
DEVICE_INFO	5 months 27 days	No description

Najpopularniejsze Kursy w maju

Zobacz darmowe lekcje