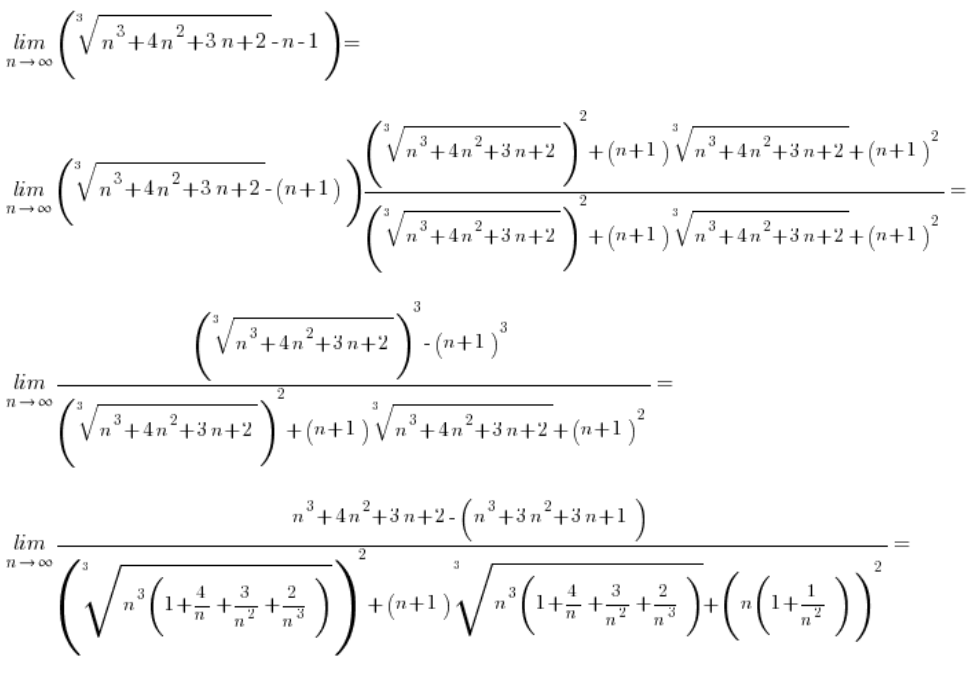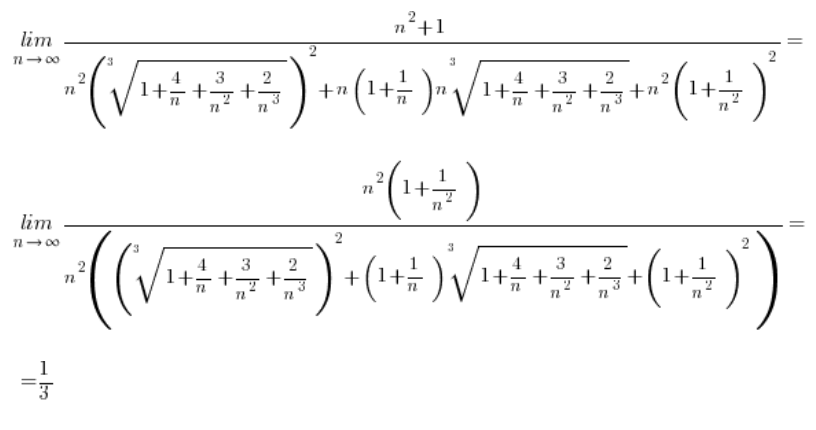三次根的极限 (是不是通过共轭相乘？)
Krystian Karczyński
eTrapez网站的创始人兼负责人。
波兹南理工大学（波兰）数学专业硕士。拥有多年数学家教经验。创建了第一个eTrapez课程，这些课程在波兰全国的学生中获得了巨大的流行。
居住在什切青（波兰）。喜欢森林散步、海滩放松和划独木舟。
以前处理“普通”根号的情况是怎样的？
当我们需要计算一个极限，并且其中包含减法和根号（显然无法更简单地计算），例如：
“某物 – 某物的根号”
“某物的根号 – 某物”
“某物的根号 – 某物的根号”
我们使用一种我称之为“乘以共轭”的技巧。
我们只是将该表达式乘以其带加号的对应项，或者更准确地说，乘以一个分数，其分子和分母都是该对应项。
例如：
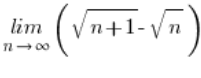我们这样乘以：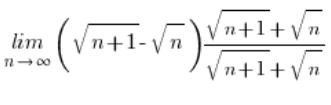
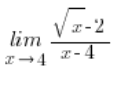我们这样乘以：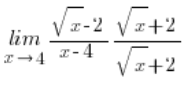
这个巧妙的技巧使我们能够得到简化乘法公式：
得到这个公式后，平方“抵消”了根号，我们就得到了一个简单的结果（好吧，有时候只是稍微长一点的简单结果）。
但是，当根号涉及到三次方根时情况又会怎样呢？比如这里：
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}标准的操作方法，即如下乘法：
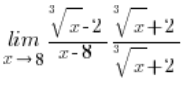
对我们没有任何帮助，因为这次在分子中得到的公式是：
平方根号不会抵消三次方根。所以我们还是会卡住。
对于三次方根的情况会是怎样？
在涉及三次方根的减法情况下，我们需要使用完全不同的公式（也是初中的内容），即：
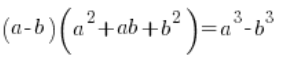
所以我们的表达式 
（其中a或b或两者都是三次方根）不会乘以
，而是乘以 
，并应用公式，立方将完成其工作，“抵消”根号。
例子 1
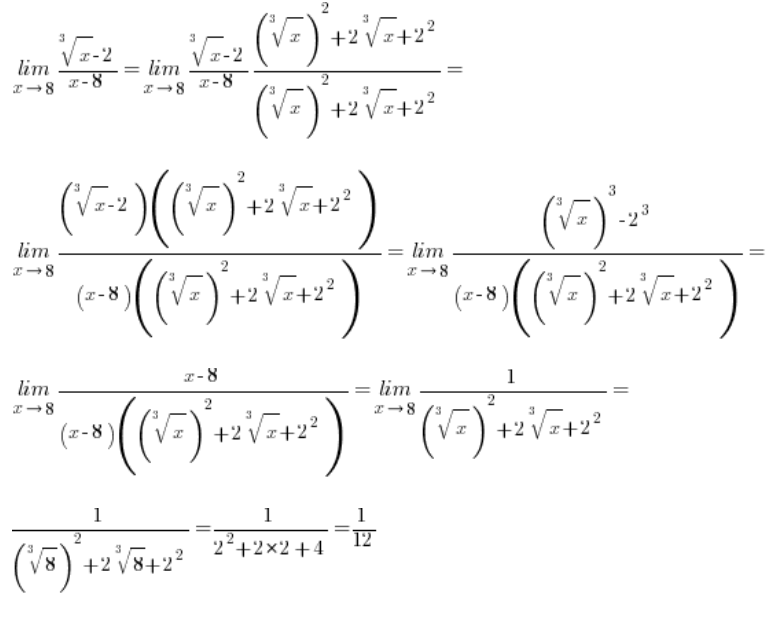
例子 2
你在寻找大学或高中级别的数学家教吗？ 或者你需要一个课程来帮助你准备高考吗？
我们是eTrapez团队。我们以清晰、简单和非常详细的方式教授数学 - 甚至可以触及到最抗拒学习的人。
我们创建了用易懂的语言解释的视频课程，可以下载到电脑、平板或手机上。你只需打开视频，就像在家教课上一样，观看和聆听。无论是白天还是夜晚，任何时候都可以。
