地点和时间
计算方向导数作为一个学习(即通过)主题,实际上紧随多变量函数的偏导数之后,大多数学生在第二学期学习这些内容。
这个主题很少被提及,因此我没有在我的偏导数课程中包含它,但它被提及的频率足够高,因此我会在博客中提到它 – 供那些需要学习方向导数的人以及那些只是好奇的人使用。然而,正如在课程中一样,今天我几乎只关注实际操作(“我该怎么做?”),而不是理论(“我到底在做什么?”)。
方向导数 – 我该怎么做?
在方向导数的情况下,我们处理的是 x 和 y 参数的同步增长,这当然对应于函数值的增长 ![]() 。
。
完成任务我们需要三样东西:
- 我们将计算方向导数的函数。
- 我们将计算方向导数的点。
- 以向量形式给出的方向。
有了上述内容,任务就变成了将向量转换为方向向量(这是解析几何的一部分,我稍后会展示如何做),然后将其代入公式:
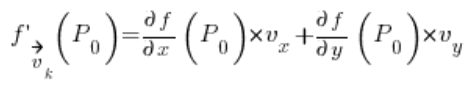
其中:
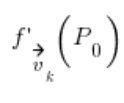 是在点
是在点 ![]() 在向量方向上的方向导数
在向量方向上的方向导数 ![]()
![]() 是我们计算方向导数的点
是我们计算方向导数的点
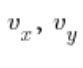 是方向向量的坐标
是方向向量的坐标
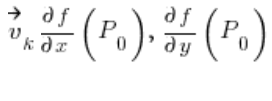 是函数的偏导数
是函数的偏导数 ![]() 在点
在点 ![]() 。
。
计算函数的方向导数 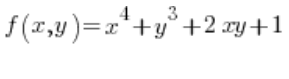 在点 P(1,2) 在方向
在点 P(1,2) 在方向 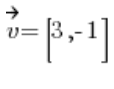 。
。
解决方案:
一切都已准备就绪,只需将向量 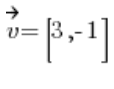 转换为方向向量。
转换为方向向量。
方向向量是具有相同方向、相同方向但长度为 1 的向量。
它通过公式计算:
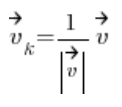
也就是说,只需将其坐标除以其长度。
所以我们计算向量的长度 ![]() :
:
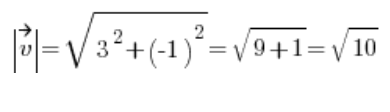
然后我们得出方向向量:
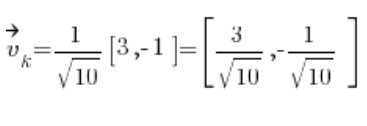
在方向导数的公式中,我们还需要函数的偏导数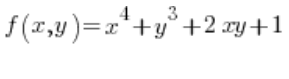 在点 P(1,2):
在点 P(1,2):
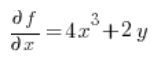
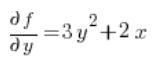
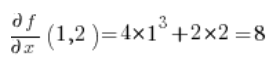
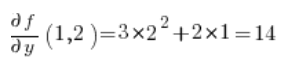
现在我们有了公式所需的一切:
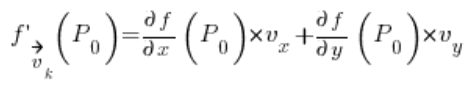
只需代入,我们就得到结果: 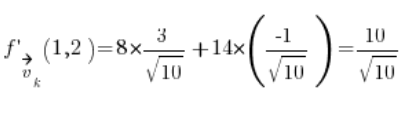 。
。
完成。
例子 2
求函数的方向导数: 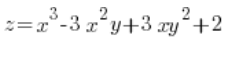 在点 P(3,1) 在从该点到点的方向 Q(6,5)。
在点 P(3,1) 在从该点到点的方向 Q(6,5)。
解决方案:
问题稍微困难一点,因为方向向量没有直接给出,但这对我们来说没什么。
我们从点 P 移动到点 Q,因此移动向量是向量 [3,4]。
现在我们通过计算向量 [3,4] 的长度来寻找方向向量:
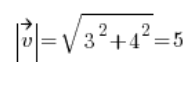
我们得到方向向量:
现在在点 (3,1) 计算偏导数:
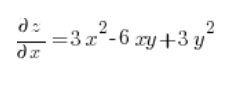
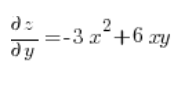
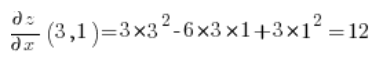
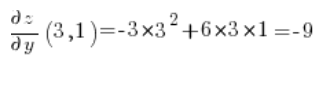
然后只需代入方向导数公式:
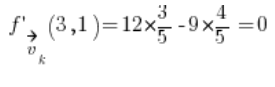
例子 3
求函数的方向导数 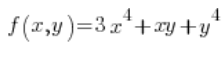 在点 (1,2) 在与 X 轴正方向成角度
在点 (1,2) 在与 X 轴正方向成角度 ![]() 的方向上。
的方向上。
解决方案:
问题看似更难,因为数据中没有给出方向向量。让我们画出整个情况:

关键是找到具有指定方向的任意向量的坐标。
我们使用事实 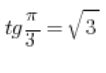 ,可以假设我们的向量具有坐标
,可以假设我们的向量具有坐标 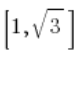 ,如图所示(只需选择任意一个具有与直线方向相同的向量):
,如图所示(只需选择任意一个具有与直线方向相同的向量):

现在我们继续老方法。
计算方向向量:
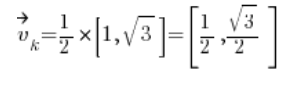
然后在点 (1,2) 计算偏导数:
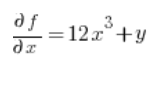
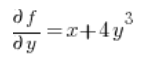
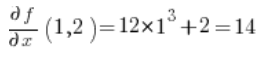
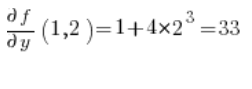
代入公式,我们得到结果
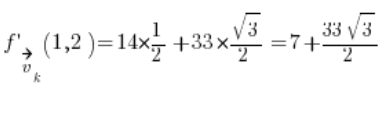
欢迎在评论中提问 – 一如既往 🙂


